Kolmannen lain mukaan aineen entropia on aina äärellinen ja lähestyy vakiota lämpötilan lähestyessä nollaa. Tämän vakion arvo on riippumaton kaikkien muiden ainetta luonnehtivien tilafunktioiden arvoista. Minkä tahansa aineen nollalämpötilan raja-arvolle voidaan vapaasti antaa mielivaltaisesti valittu arvo. Kaikille aineille ei kuitenkaan voida määrittää mielivaltaista nollalämpötila-entropiaa. Tekemiemme määritysten on oltava johdonmukaisia kokeellisesti havaittujen eri aineiden reaktioiden entropian muutosten nollalämpötilan raja-arvojen kanssa. Täysin kiteisillä aineilla nämä reaktioiden entropiat ovat kaikki nolla. Tämä ehto voidaan täyttää antamalla kunkin alkuaineen nollalämpötilan molaariselle entropialle mielivaltainen arvo ja määräämällä, että minkä tahansa yhdisteen nollalämpötilan entropia on sen muodostavien alkuaineiden nollalämpötilan entropioiden summa. Tämä laskelma yksinkertaistuu huomattavasti, jos jokaisen alkuaineen nollalämpötilaentropian annetaan olla nolla. Tämä on kolmannen lain olennainen sisältö.
Lewisin ja Randallin lausuma sisältää tämän nollaentropian vertailutilan valinnan entropioita varten määrittelemällä sen kunkin alkuaineen ”kiteiseksi tilaksi” nolla-asteessa. Tämän seurauksena minkä tahansa aineen entropia nolla-asteessa on suurempi tai yhtä suuri kuin nolla. Toisin sanoen Lewisin ja Randallin lausunto sisältää sopimuksen, joka määrittää minkä tahansa aineen entropian nollalämpötilan raja-arvon. Tältä osin Lewisin ja Randallin lausumassa tehdään olennaisesti mielivaltainen valinta, joka ei ole luonnon luontainen ominaisuus. Näemme kuitenkin, että se on ylivoimaisen kätevä valinta.
Olemme keskustelleet ensimmäisen ja toisen lain vaihtoehtoisista lausekkeista. Myös useat kolmannen lain vaihtoehtoiset lausumat ovat mahdollisia. Tarkastelemme seuraavia:
Se on mahdotonta saavuttaa absoluuttisen nollan lämpötilaa.
Tämä lausuma on yleisempi kuin Lewisin ja Randallin lausuma. Jos tarkastelemme tämän väitteen soveltamista lämpötiloihin, jotka ovat saavutettavissa yhden aineen prosesseissa, voimme osoittaa, että se sisältää Lewisin ja Randallin väitteen ja että Lewis ja Randallin väite sisältää sen.
Lämpökapasiteetin \(C_P\) ominaisuudet ovat keskeisessä asemassa näissä väitteissä. Olemme nähneet, että \(C_P\) on lämpötilan funktio. Vaikka se ei ole hyödyllistä, voimme soveltaa \(C_P\):n määrittelysuhdetta faasimuutoksessa olevaan aineeseen ja löytää \(C_P=\infty\). Jos ajattelemme ainetta, jonka lämpökapasiteetti on pienempi kuin nolla, kohtaamme ristiriidan lämpöä ja lämpötilaa koskevien perusajatustemme kanssa: Jos \(q>0\) ja \({q}/{\Delta T}<0\), on oltava \(\Delta T<0\); toisin sanoen aineen lämmittäminen aiheuttaa sen lämpötilan laskun. Lyhyesti sanottuna kehittämässämme teoriassa on premissejä, jotka edellyttävät \(C_P>0\) mille tahansa systeemille, josta voimme tehdä mittauksia.
Kuvaamme puhtaan aineen systeemiä sen paineen ja lämpötilan avulla ja tarkastelemme reversiibeleitä vakiopaine-prosesseja, joissa vain paineen ja tilavuuden välinen työ on mahdollista. Tällöin \({\left({\partial S}/{\partial T}\right)}_P={C_P}/{T}\) ja \(dS={C_PdT}/{T}\). Haluamme nyt osoittaa: Lewisin ja Randallin vaatimus, jonka mukaan entropia on aina äärellinen, edellyttää, että lämpökapasiteetti laskee nollaan, kun lämpötila laskee nollaan. (Koska aiomme osoittaa, että kolmas laki kieltää mittaukset absoluuttisessa nollapisteessä, tämä johtopäätös on johdonmukainen edellisessä kappaleessa tekemämme johtopäätöksen kanssa). Se, että lämpökapasiteetti menee nollaan, kun lämpötila menee nollaan, käy ilmi \(S={C_PdT}/{T}.\) Jos \(C_P\) ei mene nollaan, kun lämpötila menee nollaan, \(dS\) kasvaa mielivaltaisen suureksi, kun lämpötila menee nollaan, mikä on ristiriidassa Lewisin ja Randallin väitteen kanssa.
Kehittääksemme tätä tulosta eksplisiittisemmin, olkoon lämpökapasiteetit lämpötiloissa \(T\) ja nollassa \(C_P\\vasen(T\oikea)\) ja \(C_P\vasen(0\oikea)\). Koska \(C_P\left(T\right)>0\) mille tahansa \(T\ >\ 0\), on \(S\left(T\right)-S\left(T^*\right)>0\) mille tahansa \(T>T^*>0\). Koska entropia on aina äärellinen, \(\infty >S\left(T\right)-S\left(T^*\right)>0\), joten
\\ }>0\]
ja
\
Lämpötiloille nollan lähistöllä, voimme laajentaa lämpökapasiteetin mielivaltaisella tarkkuudella Taylorin sarjan polynomina \(T\):n suhteen:
\
Epäyhtälöt muuttuvat
\
Vasemmanpuoleinen ehto vaatii \(C_P\left(0\right)=0\).
Voisimme tarkastella kolmatta lakia lausumana puhtaiden aineiden lämpökapasiteeteista. Emme päätele ainoastaan, että \(C_P>0\) kaikille \(T>0\), vaan myös, että
\
Yleisemmin voimme päätellä vastaavat väitteet suljetuille palautuville systeemeille, jotka eivät ole puhtaita aineita: \({\left({\partial H}/{\partial T}\right)}_P>0\) kaikille \(T>0\), ja \({\mathop{\mathrm{lim}}_{T\to 0} T^{-1}{\left({\partial H}/{\partial T}\right)}_P=0\ }\). (Tällaisten systeemien nollalämpötilaentropiat eivät kuitenkaan ole nolla.) Alla olevassa keskustelussa kuvaamme systeemin puhtaana aineena. Voimme esittää periaatteessa samat väitteet mille tahansa systeemille; meidän tarvitsee vain korvata \(C_P\) \({\left({\partial H}/{\partial T}\right)}_P\). Lewisin ja Randallin lausekkeen mukaan entropia muuttuu vakioksi absoluuttisessa nollapisteessä riippumatta muiden termodynaamisten funktioiden arvoista. Tästä seuraa, että entropia nollassa asteessa on riippumaton paineen arvosta. Mille tahansa kahdelle paineelle, \(P_1\) ja \(P_2\), on \(S\left(P_2,0\right)-S\left(P_1,0\right)=0\). Olkoon \({P=P}_1\) ja \(P_2=P+\Delta P\) ja, meillä on
\
kaikille \(\Delta P\). Näin ollen meillä on
\
Luvussa 10 havaitsemme \({\left({\partial S}/{\partial }P\right)}_T=-{\left({\partial V}/{\partial T}\right)}_P\), joten sekä entropia että tilavuus lähestyvät nollalämpötila-arvojaan asymptoottisesti.
Kun sanomme, että absoluuttinen nollapiste on saavuttamaton, tarkoitamme, että mikään systeemi ei voi käydä läpi mitään muutosta, jossa sen loppulämpötila on nolla. Nähdäksemme, miksi absoluuttisen nollapisteen on oltava saavuttamaton, tarkastellaan prosesseja, jotka voivat laskea systeemin lämpötilaa. Yleensä meillä on käytettävissä eri lämpötiloissa olevia lämpövarastoja. Voimme valita käytettävissä olevan säiliön, jonka lämpötila on alhaisin, ja saattaa järjestelmän tähän lämpötilaan yksinkertaisella lämpökontaktilla. Tämä on triviaalia; haasteena on tietenkin lämpötilan alentaminen edelleen. Tätä varten meidän on tehtävä jokin muu muutos. Olipa tämä muutos mikä tahansa, sitä ei voida edistää lämmönvaihdolla ympäristön kanssa. Kun olemme saattaneet järjestelmän ympäristön kylmimmän käytettävissä olevan osan lämpötilaan, kaikki muu lämmönvaihto ympäristön kanssa voi olla vain haitallista. Tästä voidaan päätellä, että minkä tahansa tarkoitukseemme soveltuvan prosessin on oltava adiabaattinen. Koska adiabaattinen prosessi ei vaihda lämpöä ympäristön kanssa, \(\Delta \hat{S}=0\).
Prosessin on myös oltava mahdollinen prosessi, joten \(\Delta S+\Delta \hat{S}\ge 0\), ja koska se on adiabaattinen, \(\(\Delta S\ge 0\). Tarkastellaan reversiibeliä ja irreversiibeliä prosessia, jossa sama järjestelmä \({}^{2}\) siirtyy tilasta, jonka määrittävät \(P_1\) ja \(T_1\), toiseen tilaan, jossa paine on \(P_2\). Näiden prosessien loppulämpötilat ja entropian muutokset ovat erilaisia. Palautuvassa prosessissa \(\Delta S=0\); loppulämpötilaksi merkitään \(T_2\). Irreversiibelissä prosessissa \(\Delta S>0\); loppulämpötila on \(T^*_2\). Kuten käy ilmi, lämpötilan muutos on pienempi palautumattomassa prosessissa kuin palautuvassa prosessissa; eli \(T_2-T_1<t^*_2-t_1\)>. Vastaavasti reversiibelissä prosessissa saavutetaan alhaisempi lämpötila: \({T_2<t}^*_2\)>. Kohdasta
\
voidaan laskea näiden prosessien entropian muutokset. Reversiibelille prosessille laskemme \
Laskemme ensin
\
isotermiselle reversiibelille muutokselle tilasta \(P_1\), \(T_1\) tilaan, jonka määräävät \(P_2\) ja \(T_1\). Tässä vaiheessa \(dT\) on nolla, joten
\
Lasketaan sitten
\
isobaariselle reversiibelille muunnokselle tilasta \(P_2\), \(T_1\) tilaan \(P_2\), \(T_2\). Tässä muunnoksessa \(dP\) on nolla, ja
\
Tällöin,
\
Koska \(\(\Delta S^{rev}=0\)), reversiibeli prosessi on yksikäsitteinen; toisin sanoen systeemin loppulämpötila määräytyy annettujen arvojen \(P_1 \), \(T_1 \) ja \(P_2 \) perusteella. Löydämme \(T_2\) kaavasta
\
Ymmärtääksemme irreversiibelin prosessin entropian muutosta toteamme ensin, että tällaisia prosesseja on ääretön määrä. Loppulämpötilassa ei ole mitään ainutlaatuista. Kun \(P_1\), \(T_1\) ja \(P_2\) on annettu, loppulämpötila \(T^*_2\) voi olla mikä tahansa aineen ominaisuuksien mukainen arvo. Määrittääksemme tietyn palautumattoman prosessin meidän on määriteltävä kaikki neljä suuretta \(P_1\), \(T_1\), \(P_2\) ja \(T^*_2\). Kun tämä on kuitenkin tehty, voimme laskea irreversiibelin prosessin entropian muutoksen,
\
laskemalla entropian muutokset, kun kuljetamme systeemiä käänteisesti pitkin isotermistä kaksivaiheista polkua \(P_1\), \(T_1\) \(P_2\), \(T_1\) ja sitten isobaarista polkua pitkin \(P_2\), \(T_1\) \(P_2\), \(T^*_2\). Laskettaessa \(\Delta S^{irrev}\) tälle palautuvalle polulle \(P_1\), \(T_1\) – \(P_2\), \(T^*_2\) käytetään samaa logiikkaa kuin laskettaessa edellisessä kohdassa \(\Delta S\) palautuvalle polulle \(P_1\), \(T_1\) – \(P_2\), \(T_2\). Erona on, että \(T^*_2\) korvaa \(T_2\) lämpötilaintegraalin ylärajana. Paineintegraali on sama. Meillä on
\
Johtuen \(\Delta S^{irrev}>\Delta S^{rev}\), meillä on
\
Koska integraalit ovat samat ja positiiviset, seuraa, että \(T^*_2>T_2\), kuten edellä on väitetty.
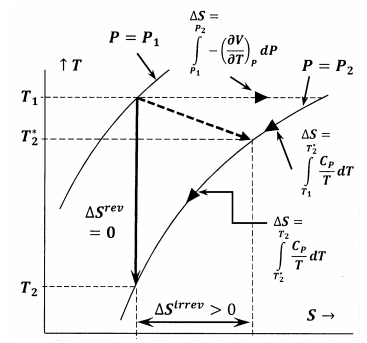
Kuvassa 6 on esitetty tässä väitteessä käsiteltyjen eri suureiden väliset suhteet. Ensiksi kuvassa 6 on esitetty systeemin kahden isobaarin kuvaaja lämpötila-entropia-avaruudessa. Toisin sanoen viiva, jossa on merkintä \(P=P_1\), kuvaa niiden lämpötila-entropiapisteiden joukkoa, joissa tasapainossa olevan järjestelmän paine on \(P_1\); viiva, jossa on merkintä \(P=P_2\), kuvaa tasapainoasentoja paineessa \(P_2\). Muut piirroksen viivat kuvaavat polkuja, joita pitkin systeemissä voi tapahtua palautuvia muutoksia vakioentropian tai vakiolämpötilan ollessa vakio. Katkoviiva edustaa palautumatonta prosessia, jossa systeemi siirtyy tilasta \(P_1\), \(T_1\) tilaan \(P_2\), \(T^*_2\). Tämä viiva on katkoviiva, joka kuvaa sitä, että systeemin lämpötila ei välttämättä ole hyvin määritelty palautumattoman prosessin aikana.
Tehokas jäähdytys voidaan saavuttaa paineenmuutoksilla, jos systeemi on kaasu. Nesteille ja kiinteille aineille \({\left({\partial V}/{\partial T}\right)}_P\) on kuitenkin pieni; näin ollen myös palautuvan paineenmuutoksen aiheuttama lämpötilan muutos on pieni. Lähellä absoluuttista nollaa olevissa lämpötiloissa lähes kaikki aineet ovat kiinteitä; tehokkaan jäähdytyksen aikaansaamiseksi on muutettava termodynaamista muuttujaa, jolle kiinteän aineen lämpötilakerroin on mahdollisimman suuri. Tarkastellaksemme yleistä ongelmaa, joka koskee systeemin lämpötilan alentamista muuttamalla jotakin muuta kuin painetta, meidän on tarkasteltava systeemiä, jossa jonkinlainen muu kuin paineen ja tilavuuden välinen työ on mahdollista. Tällaiseen systeemiin kohdistuu lisävoima, ja sen energia muuttuu tämän voiman muuttuessa.
Adiabaattinen demagnetointi
Käytännön menetelmää, jolla saavutetaan äärimmäisen alhaisia lämpötiloja, kutsutaan adiabaattiseksi demagnetoinniksi. Tässä menetelmässä hyödynnetään paramagneettisten kiinteiden aineiden ominaisuuksia. Tällaisissa kiinteissä aineissa yksittäisiin atomeihin paikallistetut parittomat elektronit synnyttävät magneettisen momentin. Kvanttimekaniikka johtaa tärkeisiin päätelmiin tällaisten magneettisten momenttien ja sovelletun magneettikentän välisestä vuorovaikutuksesta: Sovelletussa magneettikentässä yksittäisen atomin magneettinen momentti on kvantittunut. Yksinkertaisimmassa tapauksessa se voi suuntautua vain kahteen suuntaan; sen on oltava joko yhdensuuntainen tai vastakkainen sovellettuun magneettikenttään nähden. Kun atomin magneettinen momentti on samansuuntainen magneettikentän kanssa, systeemin energia on pienempi kuin silloin, kun suuntaus on vastakkainen. Sovellettu magneettikenttä harjoittaa voimaa yksittäisiin atomeihin liittyviin magneettisiin momentteihin. Systeemin energia riippuu sovelletun magneettikentän suuruudesta.
Ennemmin kuin keskitytään adiabaattisen demagnetisaation erityistapaukseen, tarkastellaan energian ja entropian muutoksia, jotka liittyvät yleistetyn potentiaalin \({\mathit{\Phi}}_{\theta }\) ja sen yleistetyn siirtymän \(\theta\) muutoksiin. (Adiabaattisessa demagnetoinnissa \(\theta\) olisi sovellettu magneettikenttä.) Tämän systeemin palautuvien muutosten kuvaamiseen tarvitaan kolme muuttujaa. Voimme ilmaista energian ja entropian lämpötilan, paineen ja \(\theta\) funktioina:
\(E=E\left(T,P,\theta \right)\) ja \(S=S\left(T,P,\theta \right)\). Entropian kokonaisdifferentiaali sisältää termin, joka määrittää entropian riippuvuuden \(\theta\). Meillä on
\
jossa kirjoitamme \(C\left(T,P,\theta \right)\) korostaaksemme, että tämänhetkiset tarkoituksemme edellyttävät nyt, että mittaamme lämpökapasiteetin vakiopaineessa ja vakiossa \(\theta\).
Vakiopaineessa P ja vakiosiirtymässä \(\theta\) entropia riippuu lämpötilasta seuraavasti
\
Postulaatti, jonka mukaan entropian on oltava äärellinen missä tahansa lämpötilassa, merkitsee sitä, että paineesta ja \(\theta\)-lämpökapasiteetista riippuva lämpökapasiteetti muuttuu nollaksi absoluuttisessa nollassa. Toisin sanoen absoluuttisessa nollapisteessä lämpökapasiteetti häviää riippumatta P:n ja \(\theta\) arvoista. Argumentti on täsmälleen sama kuin aiemmin. Aiemmin kirjoitimme \(C_P\ vasen(0\oikea)=0\); tässä yleistetyssä tapauksessa kirjoitamme \(C\ vasen(0,P,\theta \oikea)=0\).
Vastaavasti postulaatista, jonka mukaan entropia muuttuu vakioksi absoluuttisessa nollapisteessä kaikilla muiden termodynamiikan muuttujien arvoilla, seuraa, että mille tahansa kahdelle paineelle \(P_1\) ja \(P_2\) ja mille tahansa kahdelle yleistetyn siirtymän arvolle, \(\theta }_1\) ja \(\theta }_2\),
\
ja siten, että
\ ja \
Haluamme tarkastella prosessia, jossa systeemi siirtyy alhaisimmasta ympäristöstä saatavasta lämpötilasta vielä alhaisempaan lämpötilaan. Loppulämpötilan minimoimiseksi tämä prosessi on suoritettava adiabaattisesti. Sen on myös oltava mahdollinen prosessi, jotta \(dS\ge 0\). Oletetaan nyt yksinkertaisuuden vuoksi, että prosessi suoritetaan vakiopaineessa \(P\) ja että systeemi siirtyy tilasta \(P\), \(T_1\), \({\theta }_1\) tilaan \(P\), \(T_2\), \(T_2\), \(\theta }_2\), jossa \(T_1>T_2\). Näiden kahden tilan entropiat ovat
\ ja \
Tämän prosessin entropian muutos on
\ \ \
Oletetaan nyt, että loppulämpötila on nolla; eli \(T_2=0\), joten
\ Tästä seuraa, että \
jolloin oikeanpuoleinen epätasa-arvo seuraa siitä, että \(C\left(T,P,{\theta }_1\right)>0\). Tästä seuraa, että
\
mikä on ristiriidassa Lewisin ja Randallin kolmannen lain lausuman kanssa. Oletus, että systeemi voi saavuttaa absoluuttisen nollapisteen, johtaa Lewisin ja Randallin kolmannen lain lausuman ristiriitaan. Jos Lewisin ja Randallin lausuma on siis totta, absoluuttinen nollapiste on saavuttamaton.
Käänteinenkin pätee, eli lauseesta, että absoluuttinen nollapiste on saavuttamaton, voidaan osoittaa, että Lewisin ja Randallin lausuma on totta. Tätä varten järjestämme yllä olevan yhtälön \(\Delta S\),
\ \ \
Jos nyt oletamme, että Lewisin ja Randallin väite on väärä, oikealla oleva lauseke voi olla pienempi tai yhtä suuri kuin nolla. Tällöin vasemmalla oleva integraali voi olla nolla, jolloin systeemi voi saavuttaa absoluuttisen nollapisteen. Jos Lewisin ja Randallin väite on väärä, on totta, että systeemi voi saavuttaa absoluuttisen nollapisteen. Näin ollen: Jos systeemi ei voi saavuttaa absoluuttista nollaa, Lewisin ja Randallin väite on tosi.
Kuvissa 7 ja 8 esitetään nämä ajatukset käyttäen ääriviivakuvioita lämpötila-entropia-avaruudessa. Kussakin kuvassa on kaksi ääriviivaa. Toinen näistä ääriviivoista on joukko lämpötilan ja entropian arvoja, joita pitkin paine on vakio \(P\) ja \(\theta\) on vakio \({\theta }_1\). Toinen ääriviiva on joukko lämpötilan ja entropian arvoja, joita pitkin paine on vakio \(P\) ja \(\theta\) on vakio \({\theta }_2\). Kontuuriviivan kaltevuus on
\
Koska lämpökapasiteetti on aina positiivinen, tämä kaltevuus on aina positiivinen.
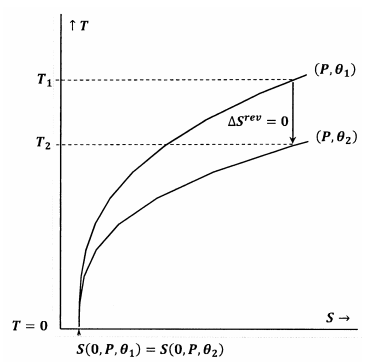
Kuvassa 7 Lewisin ja Randallin lauseke täyttyy. Kun lämpötila laskee nollaan, ääriviivat kohtaavat entropian samassa arvossa; nämä ääriviivat täyttävät suhteen
\
Adiabaattinen (pystysuora) polku ääriviivasta \(P\) ja \(\theta }_1\) kohtaa ääriviivan \(P\) ja \(\(\theta }_2\) positiivisessa lämpötilassa, \(T_2>0\). Koska tämä on ilmeisesti totta mille tahansa \(P\) ja mille tahansa \({\theta }_2\), minkä tahansa adiabaattisen prosessin lopputila on \(T_2>0\). Koska Lewisin ja Randallin lauseke täyttyy, systeemi ei voi saavuttaa absoluuttista nollaa ja päinvastoin.
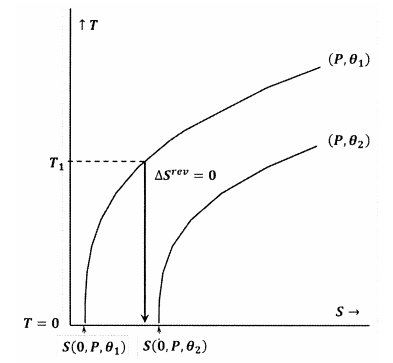
Kuvassa 8 Lewisin ja Randallin lauseketta rikotaan, koska meillä on \(S\left(0,P,{\theta }_1\right)\). Tässä tapauksessa riittävän alhaisesta alkulämpötilasta \(T_1\) alkava adiabaattinen prosessi saavuttaa absoluuttisen nollapisteen leikkaamatta \(P\) ja \({\theta }_2\) vakioiden ääriviivaa. Koska Lewisin ja Randalin lauseketta rikotaan, systeemi voi saavuttaa absoluuttisen nollapisteen ja päinvastoin.