1D- ja 3D-konvoluutiot selitetty… MS Excelillä!

Aloitimme 2D-konvoluutioista ensimmäisessä postauksessa, koska konvoluutiot saivat merkittävän suosion tietokonenäön alalla saavutettujen menestysten jälkeen. Koska tämän alan tehtävissä käytetään kuvia syötteenä, ja luonnollisissa kuvissa on yleensä kuvioita kahdessa avaruudellisessa ulottuvuudessa (korkeus ja leveys), on tavallisempaa nähdä esimerkkejä 2D-konvoluutioista kuin 1D- ja 3D-konvoluutioista.

Viime aikoina konvoluutioiden soveltamisessa luonnollisen kielen käsittelytehtäviin on kuitenkin onnistuttu valtavasti. Koska tämän alan tehtävissä käytetään tekstiä syötteenä, ja tekstissä on kuvioita yhtä avaruudellista ulottuvuutta (eli aikaa) pitkin, 1D-konvoluutiot sopivat erinomaisesti! Voimme käyttää niitä tehokkaampina vaihtoehtoina perinteisille rekursiivisille neuroverkoille (RNN), kuten LSTM:lle ja GRU:lle. Toisin kuin RNN:t, niitä voidaan käyttää rinnakkain todella nopeiden laskutoimitusten aikaansaamiseksi.

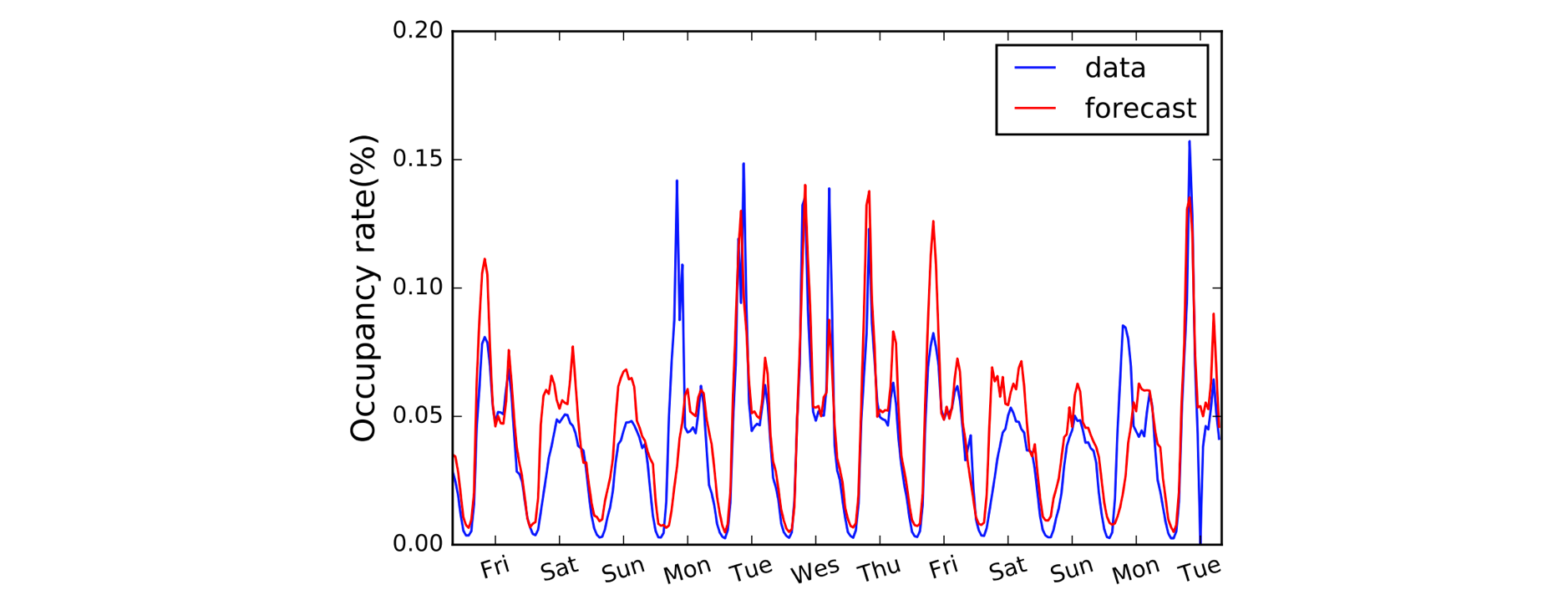
Toinen 1D-konvoluutioista hyötyvä alue on aikasarjojen mallintaminen. Kuten aiemminkin, meillä on yksi spatiaalinen ulottuvuus syöttötiedoissamme (eli aika), ja haluamme poimia kuvioita ajanjaksojen ajalta. Kutsumme tämäntyyppistä dataa usein ”peräkkäiseksi”, koska sitä voidaan tarkastella arvojen sarjana. Paikallista ulottuvuutta kutsutaan usein ajalliseksi ulottuvuudeksi. Myös 1D-konvoluutioiden käyttäminen ennen RNN:iä on melko yleistä: LSTNet-malli on esimerkki tästä, ja sen ennusteet liikenteen ennustamista varten on esitetty alla.

A, B, C. Helppo juttu, sillä (1,3,3) piste (2,0,1) = 5.

Nimeämiskäytäntöjen selkiydyttyä tarkastellaan nyt tarkemmin aritmetiikkaa. Olemme onnekkaita, sillä 1D-konvoluutio on itse asiassa vain yksinkertaistettu versio 2D-konvoluutiosta!

Työskentelemällä yhden lähtöarvon laskemisen kautta voimme soveltaa koon 3 ytimemme vastaavankokoiseen alueeseen tulomassamme vasemmalla puolella. Laskemme syöttöalueen ja ytimen ’pistetuoton’, joka lyhyesti sanottuna on pelkkä elementtituotto (eli kerrotaan väriparit), jota seuraa kokonaissumma yhden arvon saamiseksi. Tässä tapauksessa:

(1*2) + (3*0) + (3*1) = 5

Sovellamme samaa operaatiota (samalla ytimellä) syötemäärän muille alueille saadaksemme täydellisen tulostemäärän (5,6,7,2); eli liu’utamme ydintä koko syötemäärän yli. Toisin kuin 2D-konvoluutioissa, joissa liu’utamme ydintä kahteen suuntaan, 1D-konvoluutioissa liu’utamme ydintä vain yhteen suuntaan; tässä kaaviossa vasemmalle/oikealle.

Edistyneempi: 1D-konvoluutio ei ole sama kuin 1×1 2D-konvoluutio.

Koodaaminen

Yllättävää kyllä, tarvitsemme 1D-konvoluutiossamme Gluonissa olevan Conv1D lohkon. Määrittelemme ytimen muodoksi 3, ja koska työskentelemme tässä esimerkissä vain yhden ytimen kanssa, määrittelemme channels=1.

import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)

Voitamme nyt siirtää syötteemme conv-lohkoon käyttäen ennalta määritettyä ydintä.

input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>

Mitä muuttuu paddingin, striden ja dilataation myötä?

Näimme paddingin, striden ja dilataation vaikutuksen edellisessä 2D-konvoluutioita käsittelevässä postauksessa, ja se on hyvin samanlainen 1D-konvoluutioissa. Paddingin avulla padataan tällä kertaa vain yhtä ulottuvuutta (ajallista ulottuvuutta) pitkin. Kaaviomme esittää aikaa vaaka-akselilla, joten pehmustamme syöttötiedon vasemmalle ja oikealle puolelle (eikä ylä- ja alapuolelle kuten 2D-konvoluutioesimerkissä). Myös stride- ja dilation-menetelmiä käytetään vain temporaalista ulottuvuutta pitkin. Esimerkki, jossa käytetään paddingia ja strideä, näyttäisi siis seuraavalta:

Lisäämme koodiin kaksi lisäargumenttia: padding=1 ja strides=2.

conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>

Edistyneempi: Syöttötietojen mittojen on oltava tietyn järjestyksen mukaisia, jota kutsutaan asetteluksi. Oletusarvoisesti 1D-konvoluutio odottaa, että sitä sovelletaan syöttötietoihin, joiden muoto on ’NCW’, eli eräkoko (N) * kanavat (C) * leveys/aika (W). Ja 2D-konvoluutioiden oletusarvo on NCHW, eli eräkoko (N) * kanavat (C) * korkeus (H) * leveys (W). Tarkista Conv1D:n ja Conv2D:n layout-argumentti.

.