3D-rekonstruktio

Tässä käytännössä tarkoituksena on ohjelmoida tarvittava logiikka, jonka avulla kobuki-robotti voi luoda 3D-rekonstruktion kohtauksesta, jonka se vastaanottaa vasemman ja oikean kameran kautta.

Asennus

Asennetaan JdeRobot-robottiakatemian yleinen infrastruktuuri.

Miten ratkaisu suoritetaan?

Navigoi 3d_reconstruction-hakemistoon

cd exercises/3d_reconstruction

Käynnistä Gazebo kobuki_3d_reconstruction-maailmalla komennolla

roslaunch ./launch/3d_reconstruction_ros.launch

Silloin sinun on suoritettava akatemiasovellus, joka sisällyttää koodisi:

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

Miten harjoitus suoritetaan?

Harjoituksen suorittamiseksi sinun on muokattava tiedostoa MyAlgorithm.py ja lisättävä siihen koodisi, joka rekonstruoi 3d-pisteet kahdesta stereonäkymästä.

Mihin koodi lisätään?

Tiedostoon MyAlgorithm.py,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Sovelluksen ohjelmointikäyttöliittymä

• self.getImage('left') – vasemman kuvan saamiseksi
• self.getImage('right') – oikean kuvan saamiseksi
• self.point.PlotPoint(position, color) – pisteen piirtämiseksi 3d-työkalussa

Käyttöliittymässä navigoiminen

hiiripohjaisesti: Pidä hiirtä painettuna ja vedä liikkuaksesi ympäristössä. Vierittämällä voit suurentaa tai pienentää

Näppäimistöpohjainen: Nuolinäppäimillä liikkuminen ympäristössä. W- ja S-näppäimet zoomaamiseen sisään tai ulos

Teoria

Tietokonenäössä ja tietokonegrafiikassa 3D-rekonstruktio on prosessi, jossa määritetään kohteen 3D-profiili sekä tiedetään profiilin minkä tahansa pisteen 3D-koordinaatti. Rekonstruktio voidaan toteuttaa seuraavasti:

• Laitteistopohjainen: Laitteistopohjainen lähestymistapa edellyttää, että hyödynnetään rekonstruktiotehtävään soveltuvaa laitteistoa. Esimerkkeinä voidaan mainita strukturoidun valon, laseretäisyysmittarin, syvyysmittarin ja radiometristen menetelmien käyttö.

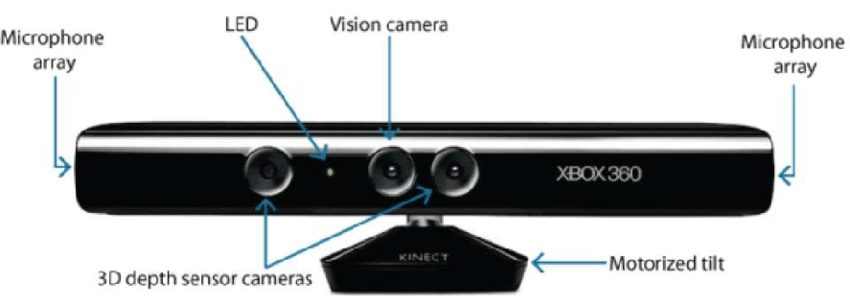
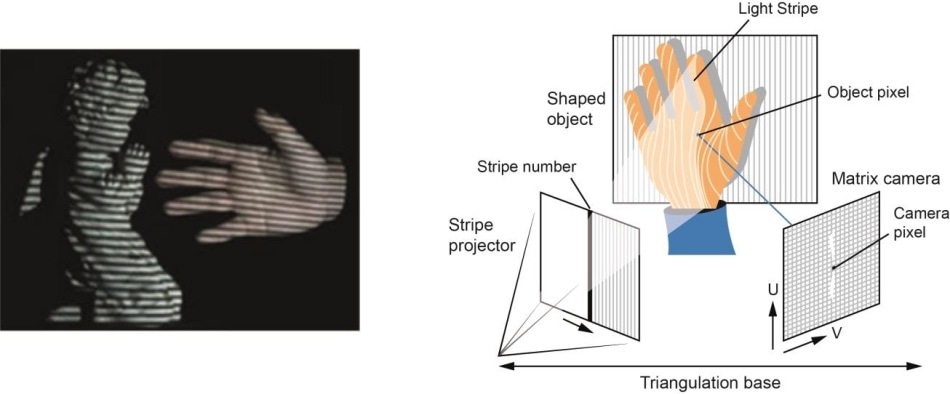
• Ohjelmistopohjainen: Ohjelmistopohjainen lähestymistapa luottaa tietokoneen laskentakykyyn kohteen 3D-ominaisuuksien määrittämisessä. Shape from shading, texture, stereo vision ja homography ovat hyviä menetelmiä.

Tässä harjoituksessa päätavoitteemme on suorittaa 3d-rekonstruktio ohjelmistopohjaisella lähestymistavalla, erityisesti stereonäköön perustuva 3d-rekonstruktio.

Epipolaarinen geometria

Kun kaksi kameraa tarkastelee 3D-kohtausta kahdesta eri asennosta, 3D-pisteiden ja niiden 2D-kuviin tehtyjen projisointien välille syntyy useita geometrisia suhteita, jotka johtavat kuvapisteiden välisiin rajoituksiin. Näiden ominaisuuksien ja rajoitusten tutkimista kutsutaan epipolaariseksi geometriaksi. Alla oleva kuva ja selitys voivat yleistää ajatusta:

Esitettäköön, että pistettä X 3d-avaruudessa kuvataan kahdesta näkymästä, ensimmäisessä näkymässä x ja toisessa x'. Projisoimalla säteet takaperin kamerakeskipisteisiinsä kuvatasojen kautta saamme tasopinnan, jota merkitään π:llä.

Esitettäköön nyt, että tiedämme vain x, voimme kysyä, miten vastaava piste x' on rajattu. Taso π määräytyy perusviivan(kameran keskipisteet yhdistävä viiva) ja x:n määrittelemän säteen avulla. Edellä esitetystä tiedämme, että tuntematonta pistettä x' vastaava säde sijaitsee pisteessä π, joten piste x' sijaitsee pisteen π ja toisen kuvatason leikkaussuoralla l'. Tätä suoraa kutsutaan epipolaarisuoraksi, joka vastaa x. Tämä suhde auttaa meitä pienentämään oikean kuvan pisteen etsintäavaruutta tasosta viivaksi. Joitakin tärkeitä määritelmiä, jotka on syytä huomioida, ovat:

• Epipolaarinen taso on kameran keskipisteet (perusviiva) ja kuvatason yhdistävän viivan leikkauspiste.

• Epipolaarinen taso on taso, joka sisältää perusviivan.

• Epipolaarinen viiva on epipolaarisen tason ja kuvatason leikkauspiste.

Stereorekonstruktio

Stereorekonstruktio on edellä esitetyn 3d-rekonstruktion erikoistapaus, jossa kaksi kuvatasoa ovat samansuuntaisia ja yhtä kaukana 3d-pisteestä, jonka haluamme piirtää.

Tässä tapauksessa molempien kuvatasojen epipolaarinen viiva on sama, ja ne ovat samansuuntaisia tasojen leveyden kanssa, mikä yksinkertaistaa rajoitustamme paremmin.

3D-rekonstruktioalgoritmi

Rekonstruktioalgoritmi koostuu kolmesta vaiheesta:

1. Tunnistetaan ominaispisteet yhdessä kuvatasossa
2. Tunnistetaan ominaispiste, joka vastaa edellä löydettyä
3. Trianguloidaan piste 3d-avaruudessa

Katsotaan niitä yksi kerrallaan

Ominaispisteiden havaitseminen

Ominaispisteiden havaitseminen on laaja tutkimusalue, jossa on jo tutkittu useita algoritmeja. Harris Corner Detection ja Shi-Tomasi-algoritmit käyttävät ominaisarvoja saadakseen hyvän ominaispisteen. Ongelmana on kuitenkin se, että tarvitsemme paljon pisteitä 3D-rekonstruktiota varten, eivätkä nämä algoritmit pysty tarjoamaan meille niin suurta määrää ominaispisteitä.

Siksi käytämme ominaispisteinä reunapisteitä. Niiden havaitsemisessa voi olla epäselvyyttä algoritmin seuraavassa vaiheessa. Mutta ongelmamme ratkeaa ottamalla reunapisteet ominaispisteiksi. Yksi todella hieno reunanilmaisin on Canny Edge Detection Algorithm. Algoritmi on varsin yksinkertainen ja luotettava reunojen tuottamisen suhteen.

Feature Point Extraction

Epipolaarisen rajoituksen käyttö todella yksinkertaistaa algoritmimme aikakompleksisuutta. Yleisissä 3d-rekonstruktio-ongelmissa meidän on generoitava epipolaarinen viiva jokaiselle pisteelle yhdessä kuvakehyksessä ja etsittävä sitten kyseisestä näyteavaruudesta vastaava piste toisessa kuvakehyksessä. Epipolaarisen viivan tuottaminen on myös meidän tapauksessamme hyvin helppoa, se on vain yhdensuuntaisen viivan iterpolointi vasemmasta kuvatasosta oikeaan kuvatasoon.

Kuvien välisen vastaavuuden tarkistamiseen liittyy monia algoritmeja, kuten neliöerojen summa tai energian minimointi. Menemättä kovin syvälle, yksinkertaisen korrelaatiosuodattimen käyttäminen riittää myös käyttötapauksessamme.

Triangulaatio

Triangulaatio on yksinkertaisimmillaan vain sen laskemista, missä 3d-piste tulee sijaitsemaan käyttäen kahta määritettyä pistettä kuvatasoissa.

Todellisuudessa kuvapisteiden sijaintia ei voida mitata tarkasti. Yleisissä kameroissa voi olla geometrisia tai fyysisiä vääristymiä. Siksi tämän virheen minimoimisen ja tarkimman 3d-pisteprojektion laskemisen taustalla on paljon matematiikkaa. Katso tästä linkistä yksinkertainen malli.

Vihjeitä

Yksinkertaisia vihjeitä, jotka auttavat sinua ratkaisemaan 3d_rekonstruktioharjoituksen. OpenCV-kirjastoa käytetään laajasti tässä harjoituksessa.

Setup

Harjoituksen API:n avulla voimme helposti hakea kuvat. Kuvien hakemisen jälkeen on myös hyvä suorittaa kuville kahdenvälinen suodatus, koska kuvissa on joitakin ylimääräisiä yksityiskohtia, joita ei tarvitse sisällyttää 3d-rekonstruktioon. Katso kuvista, miten kahdenvälisen suodatuksen suorittaminen vaikuttaa.

Korrelaatioiden laskeminen

OpenCV:ssä on jo sisäänrakennetut korrelaatiosuodattimet, joita voidaan kutsua matchTemplate():n kautta. Huolehdi ääritapauksista, kuten reunoista ja kulmista.

Yksi hyvä havainto on, että vasemmalla olevilla pisteillä on vastaavuus vasemmassa osassa ja oikealla olevilla pisteillä on vastaavuus oikeassa osassa. Tämän havainnon avulla voimme helposti nopeuttaa vastaavuuden laskemista.

Pisteiden piirtäminen

Joko manuaalinen tai OpenCV:hen perustuva funktio triangulatePoints toimii hyvin kolmiomittauksessa. Huolehdi vain kaikista matriisien muodoista ja koosta suorittaessasi algebrallisia toteutuksia.

Pitäkää mielessä yksinkertaisten 3D-koordinaattien ja homogeenisten 4D-koordinaattien välinen ero. Katso tästä videosta lisätietoja. Jakamalla täydellinen 4d-vektori yksinkertaisesti sen 4. koordinaatilla saamme 3d-koordinaatit.

Käyttäjien vaihtelevien toteutusten vuoksi käyttäjän on ehkä säädettävä kolmiopisteiden mittakaavaa ja offsetia, jotta ne saadaan näkyviin ja esitettäväksi GUI-käyttöliittymässä. 3D-koordinaattivektorin pienentäminen arvolla 500-1000 toimii hyvin. Myös offset 0-8 toimii hyvin.

Kuvitukset