Abeliaaninen ryhmä

Abeliaaninen ryhmä on ryhmä, jonka alkuaineet pendelöivät keskenään (eli kaikille alkuaineille ja ). Abeeliset ryhmät vastaavat siis ryhmiä, joilla on symmetriset kertotaulut.

Kaikki sykliset ryhmät ovat abeelisiä, mutta abeelinen ryhmä ei välttämättä ole syklinen. Kaikki abeelisen ryhmän alaryhmät ovat normaaleja. Abeelisessä ryhmässä jokainen alkio on konjugaatioluokassa itsessään, ja merkkitaulussa on mukana yhden alkion potensseja, joita kutsutaan ryhmän generaattoriksi.

Wolfram Language -ohjelmassa funktio AbelianGroup edustaa asteiden , , ….

Yleistä kaavaa, jolla voitaisiin antaa tietyn ryhmäluokituksen ei-isomorfisten äärellisten ryhmien lukumäärän, ei tunneta. Minkä tahansa annetun ryhmäjärjestyksen ei-isomorfisten abelilaisten äärellisten ryhmien lukumäärä saadaan kuitenkin kirjoittamalla muotoon

jossa ovat erillisiä alkutekijöitä, niin

jossa on partitiofunktio, joka on toteutettu Wolfram-kielessä nimellä FiniteAbelianGroupCount. :n arvot, kun , 2, … ovat 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 3, 2, …. (OEIS A000688).

Pienimmät järjestykset, joille , 2, 3, … on olemassa ei-isomorfisia abelilaisia ryhmiä ovat 1, 4, 8, 36, 16, 72, 32, 900, 216, 144, 64, 1800, 0, 288, 128, …. (OEIS A046056), jossa 0 tarkoittaa mahdottomia lukuja (eli ei jakolukujen tuloa) ei-isomorfisia abelialaisia ryhmiä. ”Puuttuvat” arvot ovat 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41, 43, 46, …. (OEIS A046064). Abelilaisten ryhmien asteittain suurimmat luvut järjestyksen funktiona ovat 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, …. (OEIS A046054), jotka esiintyvät järjestyksillä 1, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, …. (OEIS A046055).

Kroneckerin dekompositioteorema sanoo, että jokainen äärellinen abelilainen ryhmä voidaan kirjoittaa alkupotenssiryhmän järjestyksen omaavien syklisten ryhmien suorana ryhmätuotteena. Jos äärellisen ryhmän ryhmäjärjestys on alkuluku , niin on olemassa yksi ainoa abelilainen ryhmä, jonka järjestys on (merkitään ) eikä yhtään ei-abelilaista ryhmää. Jos ryhmän järjestys on alkuluku neliö , niin on olemassa kaksi abelilaista ryhmää (merkitään ja . Jos ryhmän järjestys on alkuluku kuutio , niin abelilaisia ryhmiä on kolme (merkitään , ja ), ja ryhmiä yhteensä viisi. Jos järjestys on kahden alkuluvun ja tulo, on olemassa täsmälleen yksi abelilainen ryhmä, jonka ryhmäjärjestys on (merkitään ).

Toinen mielenkiintoinen tulos on, että jos tarkoittaa ei-isomorfisten Abelin ryhmien lukumäärää, joiden ryhmäjärjestys on , niin

jossa on Riemannin zeta-funktio.

Abelin ryhmien järjestysluvut ovat 1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15, 17, 18, 19, 20, 25, … (OEIS A063966) , 2, …. varten. Srinivasan (1973) on myös osoittanut, että

jossa

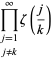			(5)
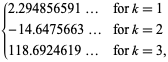			(6)

(OEIS A021002, A084892 ja A084893) ja on taas Riemannin zeta-funktio. Huomaa, että Richert (1952) antoi virheellisesti . Summat voidaan kirjoittaa myös eksplisiittisissä muodoissa

.

			(7)
			(8)
			(9)

DeKoninck ja Ivic (1980) osoittivat, että

jossa

			(11)
			(12)

(OEIS A084911) on tulo yli alkulukujen ja on taas jakofunktio.

Bounds for the number of nonisomorphic non-Abelian groups are given by Neumann (1969) and Pyber (1993).

On olemassa joukko matemaattisia vitsejä, jotka liittyvät abeliaanisiin ryhmiin (Renteln ja Dundes 2005):

Q: Mikä on violetti ja kommutoi? V: Abeliaaninen rypäle.

K: Mikä on laventeli ja kommutoi? V: Abelilainen puoliviinirypäle.

K: Mikä on violetti, pendelöi ja jota palvoo rajallinen määrä ihmisiä? A: Lopullisesti kunnioitettu abelilainen viinirypäle.

Q: Mikä on ravitsevaa ja pendelöi? V: Abelilainen keitto.