Třetí zákon postuluje, že entropie látky je vždy konečná a že se s teplotou blížící se nule blíží konstantě. Hodnota této konstanty je nezávislá na hodnotách všech ostatních stavových funkcí, které látku charakterizují. Pro jakoukoli látku můžeme libovolně zvolenou hodnotu přiřadit mezní hodnotě při nulové teplotě. Všem látkám však nemůžeme přiřadit libovolnou entropii nulové teploty. Soubor přiřazení, který provedeme, musí být v souladu s experimentálně zjištěnými mezními hodnotami změn entropie při nulové teplotě u různých látek. Pro dokonale krystalické látky jsou všechny tyto reakční entropie nulové. Tuto podmínku můžeme splnit tak, že molární entropii každého prvku při nulové teplotě přiřadíme libovolnou hodnotu a stanovíme, že entropie každé sloučeniny při nulové teplotě je součtem entropií jejích složek při nulové teplotě. Tento výpočet se značně zjednoduší, pokud necháme entropii každého prvku při nulové teplotě nulovou. To je podstatný obsah třetího zákona.
Lewisův a Randallův výrok zahrnuje tento výběr referenčního stavu nulové teploty pro entropie a specifikuje jej jako „krystalický stav“ každého prvku při nulové teplotě. V důsledku toho je entropie každé látky při nulových stupních větší nebo rovna nule. To znamená, že Lewisův a Randallův výrok obsahuje konvenci, která stanovuje mezní hodnotu entropie jakékoli látky při nulové teplotě. V tomto ohledu Lewisovo a Randallovo tvrzení obsahuje v podstatě libovolnou volbu, která není vlastní vlastností přírody. Vidíme však, že je to volba ohromně výhodná.
Probírali jsme alternativní výroky prvního a druhého zákona. Řada alternativních výroků třetího zákona je rovněž možná. Uvažujeme následující:
Není možné dosáhnout teploty absolutní nuly.
Toto tvrzení je obecnější než Lewisovo a Randallovo tvrzení. Uvážíme-li aplikaci tohoto tvrzení na teploty dosažitelné při procesech zahrnujících jednu látku, můžeme ukázat, že z něj vyplývá Lewisovo a Randallovo tvrzení a že je jím implikováno.
Vlastnosti tepelné kapacity, \(C_P\), hrají v těchto argumentech ústřední roli. Viděli jsme, že \(C_P\) je funkcí teploty. I když to není užitečné, můžeme definiční vztah pro \(C_P\) aplikovat na látku procházející fázovým přechodem a zjistit \(C_P=\infty\). Pokud uvažujeme o látce, jejíž tepelná kapacita je menší než nula, narazíme na rozpor našich základních představ o teple a teplotě: Jestliže \(q>0\) a \({q}/{\Delta T}<0\), musíme mít \(\Delta T<0\); to znamená, že zahřívání látky způsobuje pokles její teploty. Stručně řečeno, teorie, kterou jsme vytvořili, obsahuje předpoklady, které vyžadují \(C_P>0\) pro jakoukoli soustavu, na které můžeme provádět měření.
Charakterizujme soustavu čisté látky jejím tlakem a teplotou a uvažujme vratné procesy s konstantním tlakem, při kterých je možná pouze tlakově-objemová práce. Pak \({\levice({\část S}/{\část T}\pravice)}_P={C_P}/{T}\) a \(dS={C_PdT}/{T}\). Nyní chceme ukázat: Lewisova a Randallova podmínka, že entropie je vždy konečná, vyžaduje, aby tepelná kapacita klesla na nulu, když teplota klesne na nulu. (Protože se chystáme ukázat, že třetí zákon zakazuje měření při absolutní nule, je tento závěr v souladu s naším závěrem v předchozím odstavci). To, že tepelná kapacita klesá k nule, když teplota klesá k nule, je zřejmé z \(S={C_PdT}/{T}.\) Jestliže \(C_P\) neklesá k nule, když teplota klesá k nule, \(dS\) se stává libovolně velkým, když teplota klesá k nule, což je v rozporu s Lewisovým a Randallovým tvrzením.
Pro explicitnější rozvinutí tohoto výsledku nechť jsou tepelné kapacity při teplotách \(T\) a nule \(C_P\levá(T\pravá)\) a \(C_P\levá(0\pravá)\). Protože \(C_P\left(T\right)>0\) pro libovolné \(T\ >\ 0\), máme \(S\left(T\right)-S\left(T^*\right)>0\) pro libovolné \(T>T^*>0\). Protože entropie je vždy konečná, \(\infty >S\left(T\right)-S\left(T^*\right)>0\), takže
\ }>0\]
a
\
pro teploty v okolí nuly, můžeme tepelnou kapacitu s libovolnou přesností rozšířit jako polynom Taylorovy řady v \(T\):
\
Nerovnosti se stávají
\
Podmínka vlevo vyžaduje \(C_P\left(0\right)=0\).
Na třetí zákon bychom se mohli dívat jako na výrok o tepelných kapacitách čistých látek. Z toho můžeme odvodit nejen to, že \(C_P>0\) pro všechny \(T>0\), ale také to, že
\
Obecněji můžeme odvodit odpovídající tvrzení pro uzavřené reverzibilní systémy, které nejsou čistými látkami: \({\left({\partial H}/{\partial T}\right)}_P>0\) pro všechny \(T>0\) a \({\mathop{\mathrm{lim}}_{T\to 0} T^{-1}{\left({\partial H}/{\partial T}\right)}_P=0\ }\). (Entropie při nulové teplotě takových systémů však nejsou nulové.) V následující diskusi popisujeme systém jako čistou látku. V podstatě stejné argumenty můžeme použít pro libovolnou soustavu; stačí pouze nahradit \(C_P\) za \({\left({\partial H}/{\partial T}\right)}_P\). Lewisovo a Randallovo tvrzení tvrdí, že entropie je při absolutní nule konstantní bez ohledu na hodnoty ostatních termodynamických funkcí. Z toho vyplývá, že entropie při nulových stupních nezávisí na hodnotě tlaku. Pro libovolné dva tlaky, \(P_1\) a \(P_2\), platí \(S\levá(P_2,0\pravá)-S\levá(P_1,0\pravá)=0\). Necháme-li \({P=P}_1\) a \(P_2=P+\Delta P\) a, máme
\
pro libovolné \(\Delta P\). Proto máme
\
V kapitole 10 najdeme \({\levá({\část S}/{\část }P\pravá)}_T=-{\levá({\část V}/{\část T}\pravá)}_P\), takže entropie i objem se asymptoticky blíží svým hodnotám při nulové teplotě.
Když říkáme, že absolutní nula je nedosažitelná, máme na mysli, že žádný systém nemůže projít žádnou změnou, při níž by jeho konečná teplota byla nulová. Abychom pochopili, proč musí být absolutní nula nedosažitelná, uvažujme procesy, které mohou snížit teplotu systému. Obecně máme k dispozici zásobníky tepla o různých teplotách. Můžeme si vybrat dostupný zásobník, jehož teplota je nejnižší, a jednoduchým tepelným kontaktem přivést systém na tuto teplotu. Tolik je triviální; je zřejmé, že úkolem je snížit teplotu dále. Abychom toho dosáhli, musíme provést nějakou další změnu. Ať už je tato změna jakákoli, nelze ji podpořit výměnou tepla s okolím. Jakmile jsme systém přivedli na teplotu nejchladnější dostupné části okolí, může být jakákoli další výměna tepla s okolím pouze kontraproduktivní. Docházíme k závěru, že každý proces vhodný pro náš účel musí být adiabatický. Protože adiabatický proces nevyměňuje žádné teplo s okolím, \(\Delta \hat{S}=0\).
Proces musí být také možný, takže \(\Delta S+\Delta \hat{S}\ge 0\), a protože je adiabatický, \(\Delta S\ge 0\). Uvažujme reverzibilní proces a ireverzibilní proces, ve kterém stejná soustava\({}^{2}\) přechází ze stavu určeného \(P_1\) a \(T_1\) do druhého stavu, ve kterém je tlak \(P_2\). Konečné teploty a změny entropie těchto procesů se liší. Pro vratný proces je \(\Delta S=0\); konečnou teplotu označujeme jako \(T_2\). Pro nevratný proces je \(\Delta S>0\); konečnou teplotu označujeme jako \(T^*_2\). Ukazuje se, že změna teploty je u nevratného procesu menší než u procesu vratného, tj. \(T_2-T_1<t^*_2-t_1\)>. Ekvivalentně tak reverzibilní proces dosahuje nižší teploty: \({T_2<t}^*_2\)>. Z
\
můžeme vypočítat změny entropie pro tyto procesy. Pro reverzibilní proces vypočítáme \
Pro to nejprve vypočítáme
\
pro izotermickou reverzibilní transformaci ze stavu \(P_1\), \(T_1\) do stavu určeného \(P_2\) a \(T_1\). Pro tento krok je \(dT\) nulové, a tak
\
Poté vypočítáme
\
pro izobarickou vratnou transformaci ze stavu \(P_2\), \(T_1\) do stavu \(P_2\), \(T_2\). Pro tuto přeměnu je \(dP\) nulové a
\
Pak,
\
Protože \(\Delta S^{rev}=0\), je vratný proces jedinečný; to znamená, že při daných \(P_1\), \(T_1\) a \(P_2\) je určena konečná teplota systému. Zjistíme \(T_2\) z
\
Pro pochopení změny entropie pro nevratný proces si nejprve všimneme, že takových procesů je nekonečně mnoho. Na konečné teplotě není nic jedinečného. Při daných hodnotách \(P_1\), \(T_1\) a \(P_2\) může mít konečná teplota \(T^*_2\) jakoukoli hodnotu odpovídající vlastnostem látky. Chceme-li specifikovat konkrétní nevratný proces, musíme specifikovat všechny čtyři veličiny \(P_1\), \(T_1\), \(P_2\) a \(T^*_2\). Poté, co jsme tak učinili, můžeme vypočítat změnu entropie pro nevratný proces,
\
výpočtem změn entropie, když systém reverzibilně přenášíme po izotermické dvoustupňové dráze z \(P_1\), \(T_1\) do \(P_2\), \(T_1\) a pak po izobarické dráze z \(P_2\), \(T_1\) do \(P_2\), \(T^*_2\). Výpočet \(\Delta S^{irrev}\) pro tuto vratnou cestu z \(P_1\), \(T_1\) do \(P_2\), \(T^*_2\) používá stejnou logiku jako výpočet \(\Delta S\) pro vratnou cestu z \(P_1\), \(T_1\) do \(P_2\), \(T_2\). Rozdíl je v tom, že \(T^*_2\) nahrazuje \(T_2\) jako horní mez v teplotním integrálu. Tlakový integrál je stejný. Máme
\
Z \(\Delta S^{irrev}>\Delta S^{rev}\) máme
\
Protože integrály jsou stejné a kladné, vyplývá z toho, že \(T^*_2>T_2\), jak jsme tvrdili výše.
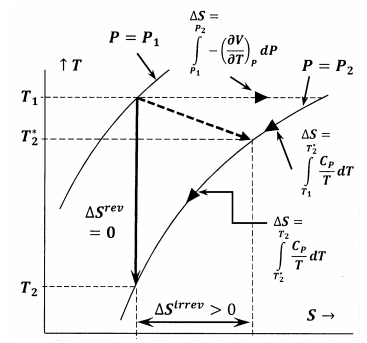
Obrázek 6 ukazuje vztahy mezi jednotlivými veličinami diskutovanými v této úvaze. V prvním případě obrázek 6 ukazuje graf dvou izobar systému v prostoru teplota-entropie. To znamená, že přímka označená \(P=P_1\) znázorňuje množinu teplotně-entropických bodů, v nichž má rovnovážný systém tlak \(P_1\); přímka označená \(P=P_2\) znázorňuje rovnovážné polohy při tlaku \(P_2\). Ostatní čáry v tomto náčrtu znázorňují dráhy, po kterých může systém procházet vratnými změnami při konstantní entropii nebo konstantní teplotě. Tečkovaná čára představuje nevratný proces, při kterém systém přechází ze stavu určeného \(P_1\), \(T_1\) do stavu určeného \(P_2\), \(T^*_2\). Tato čára je tečkovaná, aby znázornila skutečnost, že teplota systému nemusí být během nevratného procesu dobře definována.
Efektivního ochlazení lze dosáhnout pomocí změn tlaku, pokud je systém plynný. Pro kapaliny a pevné látky je však \({\levice({\část V}/{\část T}\pravá)}_P\) malá; v důsledku toho je malá i změna teploty při vratné změně tlaku. Při teplotách blízkých absolutní nule jsou téměř všechny látky pevné; abychom dosáhli účinného ochlazení, musíme změnit termodynamickou veličinu, pro kterou je teplotní koeficient pevné látky co největší. Abychom se mohli zabývat obecným problémem snižování teploty systému změnou něčeho jiného než tlaku, musíme uvažovat systém, ve kterém je možná nějaká forma netlakově-objemové práce. Na takovou soustavu působí dodatečná síla a její energie se mění se změnou této síly.
Adiabatická demagnetizace
Praktická metoda, kterou se dosahuje extrémně nízkých teplot, se nazývá adiabatická demagnetizace. Tato metoda využívá vlastností paramagnetických pevných látek. V takových pevných látkách vznikají díky nepárovým elektronům lokalizovaným na jednotlivých atomech magnetické momenty. Kvantová mechanika vede k důležitým závěrům o interakci mezi těmito magnetickými momenty a přiloženým magnetickým polem: V přiloženém magnetickém poli je magnetický moment jednotlivého atomu kvantován. V nejjednodušším případě může být uspořádán pouze ve dvou směrech; musí být buď rovnoběžný, nebo protiběžný k přiloženému magnetickému poli. Když je magnetický moment atomu rovnoběžný s magnetickým polem, je energie systému menší, než když je uspořádání protiběžné. Přiložené magnetické pole působí silou na magnetické momenty spojené s jednotlivými atomy. Energie systému závisí na velikosti přiloženého magnetického pole.
Nezaměřujme se na konkrétní případ adiabatické demagnetizace, ale uvažujme změny energie a entropie spojené se změnami zobecněného potenciálu \({\mathit{\Phi}}_{\theta }\) a jeho zobecněného posunu \(\theta\). (Pro adiabatickou demagnetizaci by \(\theta\) bylo přiložené magnetické pole.) K popisu vratných změn v tomto systému jsou zapotřebí tři proměnné. Energii a entropii můžeme vyjádřit jako funkce teploty, tlaku a \(\theta\):
\(E=E\left(T,P,\theta \right)\) a \(S=S\left(T,P,\theta \right)\). Celkový diferenciál entropie obsahuje člen, který určuje závislost entropie na \(\theta\). Máme
\
kde píšeme \(C\left(T,P,\theta \right)\), abychom zdůraznili, že naše současné účely nyní vyžadují, abychom měřili tepelnou kapacitu při konstantním tlaku a konstantním \(\theta\).
Při konstantním tlaku P a konstantním posunu \(\theta\) závisí entropie na teplotě jako
\
Postulát, že entropie je konečná při jakékoli teplotě, znamená, že tepelná kapacita závislá na tlaku a \(\theta\) se stává nulovou při absolutní nule. To znamená, že při absolutní nule tepelná kapacita mizí bez ohledu na hodnoty P a \(\theta\). Argument je naprosto stejný jako dříve. Dříve jsme psali \(C_P\left(0\right)=0\); pro tento zobecněný případ píšeme \(C\left(0,P,\theta \right)=0\).
Podobně z postulátu, že entropie je konstantní při absolutní nule pro všechny hodnoty ostatních termodynamických veličin, vyplývá, že pro libovolné dva tlaky \(P_1\) a \(P_2\) a pro libovolné dvě hodnoty zobecněného posunu, \({\theta }_1\) a \({\theta }_2\),
\
a tedy že
\ a \
Chceme uvažovat proces, při kterém systém přechází z nejnižší teploty dostupné v okolí na teplotu ještě nižší. Aby se minimalizovala konečná teplota, musí tento proces probíhat adiabaticky. Musí to být také možný proces, takže \(dS\ge 0\). Pro zjednodušení nyní předpokládejme, že tento proces probíhá za konstantního tlaku \(P\) a že systém přechází ze stavu určeného \(P\), \(T_1\), \({\theta }_1\) do stavu určeného \(P\), \(T_2\), \({\theta }_2\), kde \(T_1>T_2\). Entropie těchto dvou stavů jsou
\ a \
Změna entropie pro tento proces je
\ \
Předpokládejme nyní, že konečná teplota je nulová; to znamená, že \(T_2=0\), takže
\ Z toho vyplývá, že \
kde nerovnost vpravo vyplývá z toho, že \(C\left(T,P,{\theta }_1\right)>0\). Z toho vyplývá, že
\
což je v rozporu s Lewisovým a Randallovým tvrzením třetího zákona. Předpoklad, že systém může dosáhnout absolutní nuly, vede k rozporu Lewisova a Randallova tvrzení třetího zákona. Je-li tedy Lewisův a Randallův výrok pravdivý, je absolutní nula nedosažitelná.
Platí to i obráceně, to znamená, že z tvrzení, že absolutní nula je nedosažitelná, můžeme ukázat, že Lewisův a Randallův výrok je pravdivý. Za tím účelem upravíme výše uvedenou rovnici pro \(\Delta S\),
\ \
Předpokládáme-li nyní, že Lewisovo a Randallovo tvrzení je nepravdivé, může být výraz vpravo menší nebo roven nule. Integrál vlevo pak může být nulový, a v takovém případě může systém dosáhnout absolutní nuly. Je-li Lewisovo a Randallovo tvrzení nepravdivé, platí, že soustava může dosáhnout absolutní nuly. Z toho vyplývá, že Pokud systém nemůže dosáhnout absolutní nuly, je Lewisovo a Randallovo tvrzení pravdivé.
Obrázky 7 a 8 znázorňují tyto myšlenky pomocí obrysových grafů v prostoru teplota-entropie. Na každém obrázku jsou znázorněny dvě obrysové čáry. Jedna z těchto obrysových čar je souborem hodnot teploty a entropie, podél nichž je tlak konstantní na úrovni \(P\) a \(\theta\) je konstantní na úrovni \({\theta }_1\). Druhá obrysová čára je souborem hodnot teploty a entropie, podél nichž je tlak konstantní při \(P\) a \(\theta\) je konstantní při \({\theta }_2\). Sklon obrysové přímky je
\
Protože tepelná kapacita je vždy kladná, je tento sklon vždy kladný.
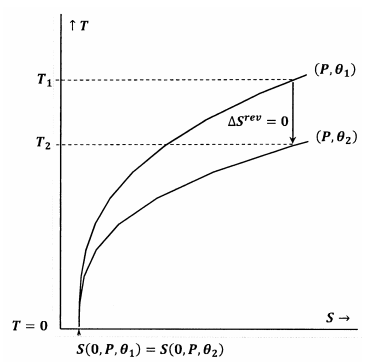
Na obrázku 7 je splněno Lewisovo a Randallovo tvrzení. Když teplota klesne na nulu, obrysové čáry se setkají při stejné hodnotě entropie; tyto obrysy splňují vztah
\
Adiabatická (vertikální) dráha z obrysu pro \(P\) a \({\theta }_1\) se setká s obrysem pro \(P\) a \({\theta }_2\) při kladné teplotě, \(T_2>0\). Protože to zjevně platí pro libovolné \(P\) a libovolné \({\theta }_2\), bude mít konečný stav pro každý adiabatický proces hodnotu \(T_2>0\). Protože je splněno Lewisovo a Randallovo tvrzení, nemůže systém dosáhnout absolutní nuly a naopak.
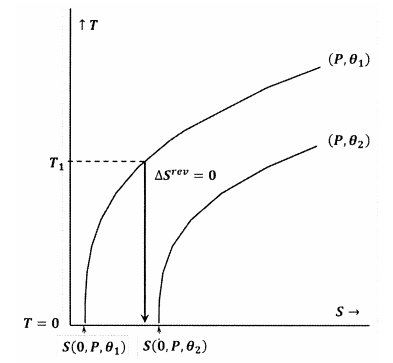
Na obrázku 8 je Lewisovo a Randallovo tvrzení porušeno, protože máme \(S\left(0,P,{\theta }_1\right)\). V tomto případě adiabatický proces zahájený z dostatečně nízké počáteční teploty \(T_1\) dosáhne absolutní nuly, aniž by protnul obrys pro konstanty \(P\) a \({\theta }_2\). Protože Lewisovo a Randalovo tvrzení je porušeno, může systém dosáhnout absolutní nuly a naopak.
.