V prvním příspěvku jsme začali s 2D konvolucemi, protože konvoluce získaly značnou popularitu po úspěších v oblasti počítačového vidění. Protože úlohy v této oblasti používají jako vstupy obrázky a přirozené obrázky mají obvykle vzory podél dvou prostorových rozměrů (výšky a šířky), je častější vidět příklady 2D konvolucí než 1D a 3D konvolucí.
V poslední době se však objevilo obrovské množství úspěchů při použití konvolucí také v úlohách zpracování přirozeného jazyka. Protože úlohy v této oblasti používají jako vstupy text a text má vzory podél jediné prostorové dimenze (tj. času), 1D konvoluce se skvěle hodí! Můžeme je použít jako efektivnější alternativu k tradičním rekurentním neuronovým sítím (RNN), jako jsou LSTM a GRU. Na rozdíl od RNN je lze spouštět paralelně a provádět tak opravdu rychlé výpočty.
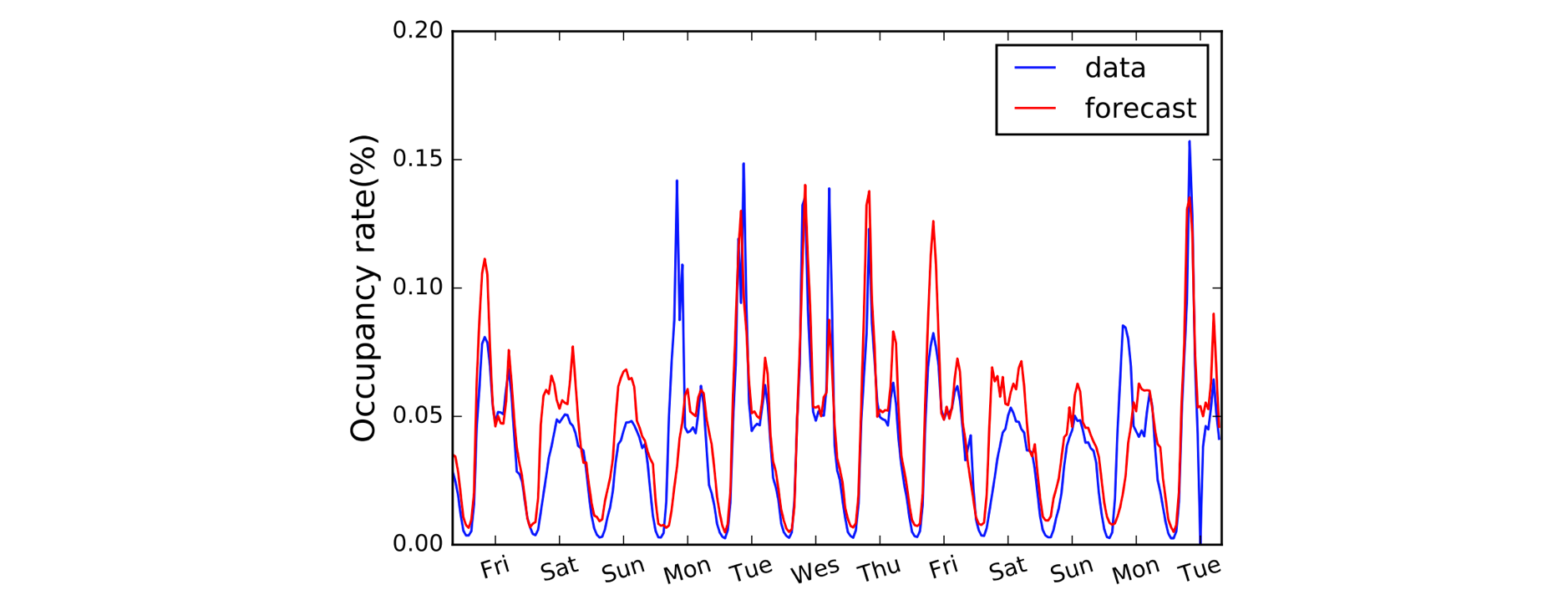
Další oblastí, která těží z 1D konvolucí, je modelování časových řad. Stejně jako dříve máme na vstupních datech jedinou prostorovou dimenzi (tj. čas) a chceme zachytit vzory v průběhu časových období. Tento typ dat často nazýváme „sekvenční“, protože na ně lze nahlížet jako na posloupnost hodnot. A prostorovou dimenzi často nazýváme „časovou“ dimenzí. Použití 1D konvolucí před RNN je také poměrně běžné: příkladem je model LSTNet, jehož předpovědi pro předpověď dopravy jsou uvedeny níže.
A, B, C. Je to jednoduché, protože (1,3,3) tečka (2,0,1) = 5.
Po vyjasnění konvencí pojmenování se nyní podívejme blíže na aritmetiku. Máme štěstí, protože 1D konvoluce jsou vlastně jen zjednodušenou verzí 2D konvoluce!

Pracujeme-li s výpočtem jediné výstupní hodnoty, můžeme naše jádro velikosti 3 aplikovat na ekvivalentně velkou oblast na levé straně naší vstupní matice. Vypočítáme „bodový součin“ vstupní oblasti a jádra, což je, abychom to shrnuli, pouze součin prvků (tj. vynásobíme dvojice barev), po kterém následuje globální součet, abychom získali jedinou hodnotu. V tomto případě tedy:
(1*2) + (3*0) + (3*1) = 5
Stejnou operaci (se stejným jádrem) použijeme na ostatní oblasti vstupního pole, abychom získali kompletní výstupní pole (5,6,7,2); tj. posuneme jádro po celém vstupním poli. Na rozdíl od 2D konvolucí, kde posouváme jádro ve dvou směrech, u 1D konvolucí posouváme jádro pouze v jednom směru; v tomto schématu vlevo/vpravo.
Pokročilé: 1D konvoluce není totéž jako 1×1 2D konvoluce.
Kódování věcí nahoru
Překvapivě budeme pro naši 1D konvoluci potřebovat blok Conv1D v Gluonu. Definujeme tvar jádra jako 3, a protože v tomto příkladu pracujeme pouze s jedním jádrem, zadáme channels=1.
import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)
Nyní můžeme předat náš vstup do bloku conv pomocí předdefinovaného jádra.
input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>
Co se změní s paddingem, stride a dilatací?
Vliv paddingu, stride a dilatace jsme viděli v minulém příspěvku o 2D konvolucích a u 1D konvolucí je to velmi podobné. U paddingu tentokrát paddujeme pouze podél jediné dimenze (časové dimenze). Náš diagram představuje čas napříč vodorovnou osou, takže padujeme vlevo a vpravo od vstupních dat (a ne nad a pod jako v příkladu 2D konvoluce). V případě krokování a dilatace je také aplikujeme pouze podél časové dimenze. Příklad s paddingem a stride by tedy vypadal takto:

V kódu přidáme dva další argumenty: padding=1 a strides=2.
conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>
Pokročilé: rozměry vstupních dat musí odpovídat určitému pořadí, které se nazývá rozložení. Ve výchozím nastavení 1D konvoluce očekává, že bude použita na vstupní data formátu „NCW“, tj. velikost dávky (N) * kanály (C) * šířka/čas (W). A pro 2D konvoluce je výchozí formát NCHW, tj. velikost dávky (N) * kanály (C) * výška (H) * šířka (W). Podívejte se na argument
layoutuConv1DaConv2D.
.