3D rekonstrukce

V tomto cvičení je záměrem naprogramovat potřebnou logiku, aby robot kobuki mohl generovat 3D rekonstrukci scény, kterou přijímá prostřednictvím své levé a pravé kamery.

Instalace

Instalace obecné infrastruktury robotické akademie JdeRobot.

Jak spustit své řešení?

Přejděte do adresáře 3d_reconstruction

cd exercises/3d_reconstruction

Spustit Gazebo se světem kobuki_3d_reconstruction pomocí příkazu

roslaunch ./launch/3d_reconstruction_ros.launch

Poté musíte spustit akademickou aplikaci, která bude obsahovat váš kód:

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

Jak provést cvičení?

Pro provedení cvičení musíte upravit soubor MyAlgorithm.py a vložit do něj svůj kód, který rekonstruuje 3d body ze dvou stereopohledů.

Kam vložit kód?

V souboru MyAlgorithm.py,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Aplikační programové rozhraní

• self.getImage('left') – pro získání levého obrazu
• self.getImage('right') – pro získání pravého obrazu
• self.point.PlotPoint(position, color) – pro vykreslení bodu v 3d nástroji

Navigace v grafickém rozhraní

Na základě myši: Podržením a tažením se pohybujete po prostředí. Posouváním můžete přibližovat nebo oddalovat obraz

Na základě klávesnice: Klávesy se šipkami pro pohyb po prostředí. Klávesy W a S pro přiblížení nebo oddálení

Teorie

V počítačovém vidění a počítačové grafice je 3D rekonstrukce proces určování 3D profilu objektu a také znalost 3D souřadnice libovolného bodu na profilu. Rekonstrukce lze dosáhnout následujícím způsobem:

• Na základě hardwaru: Hardwarový přístup vyžaduje, abychom využili hardware specifický pro úlohu rekonstrukce. Jako příklad lze uvést použití strukturovaného světla, laserového dálkoměru, hloubkoměru a radiometrických metod.

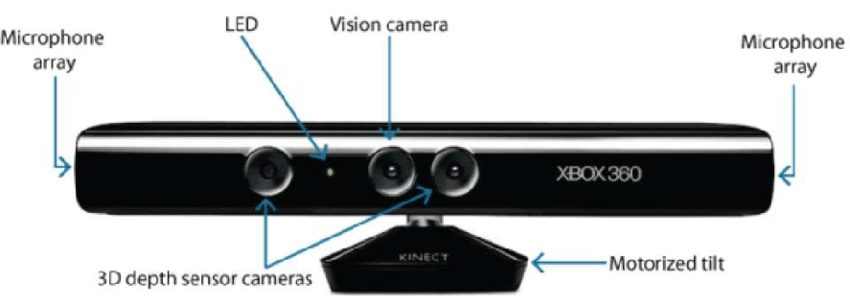
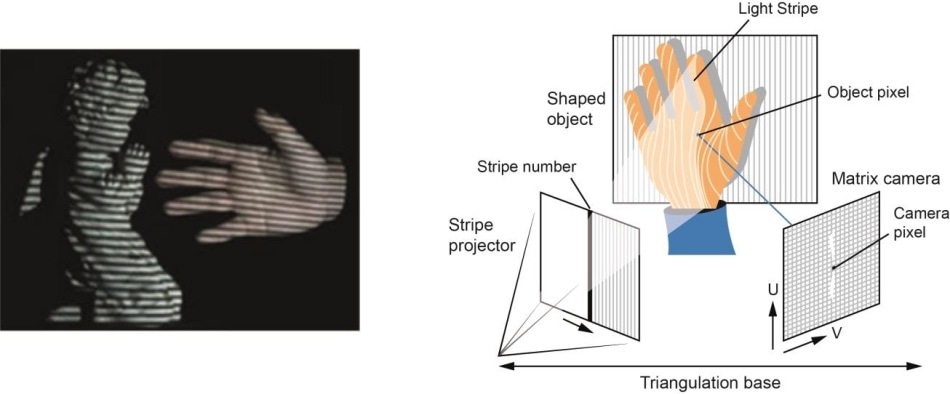
• Softwarově založená: Přístup založený na softwaru spoléhá při určování 3D vlastností objektu na výpočetní schopnosti počítače. Tvar ze stínování, textury, stereo vidění a homografie jsou některé dobré metody.

V tomto cvičení je naším hlavním cílem provést 3D rekonstrukci pomocí Softwarového přístupu, zejména 3D rekonstrukci pomocí stereo vidění.

Epipolární geometrie

Když dvě kamery sledují 3D scénu ze dvou různých pozic, existuje řada geometrických vztahů mezi 3D body a jejich projekcemi na 2D obrazy, které vedou k omezením mezi obrazovými body. Studium těchto vlastností a omezení se nazývá epipolární geometrie. Níže uvedený obrázek a vysvětlení může tuto myšlenku zobecnit:

Předpokládejme, že bod X ve 3d prostoru je zobrazen ve dvou pohledech, v bodě x v prvním a x' ve druhém. Zpětným promítnutím paprsků do jejich středů v kameře přes obrazové roviny získáme rovinnou plochu označenou π.

Předpokládáme-li nyní, že známe pouze bod x, můžeme se ptát, jak je příslušný bod x' omezen. Plocha π je určena základní linií(přímkou spojující středy kamer) a paprskem určeným x. Z výše uvedeného víme, že paprsek odpovídající neznámému bodu x' leží v π, tudíž bod x' leží na přímce průsečíku l' π s druhou obrazovou rovinou. Tato přímka se nazývá epipolární přímka odpovídající x. Tento vztah nám pomáhá redukovat prostor hledání bodu v pravém obraze, a to z roviny na přímku. Některé důležité definice, které je třeba si uvědomit, jsou:

• Epipolární rovina je průsečík přímky spojující středy kamery (základní linie) s rovinou obrazu.

• Epipolární rovina je rovina obsahující základní linii.

• Epipolární přímka je průsečík epipolární roviny s rovinou obrazu.

Stereo rekonstrukce

Stereo rekonstrukce je zvláštní případ výše uvedené 3d rekonstrukce, kdy jsou obě roviny obrazu navzájem rovnoběžné a stejně vzdálené od 3d bodu, který chceme vykreslit.

V tomto případě jsou epipolární čáry pro obě obrazové roviny stejné a jsou rovnoběžné se šířkou rovin, což lépe zjednodušuje naše omezení.

Algoritmus 3D rekonstrukce

Algoritmus rekonstrukce se skládá ze tří kroků:

1. Detekce příznakových bodů v jedné rovině obrazu
2. Detekce příznakového bodu odpovídajícího výše nalezenému bodu
3. Triangulace bodu ve 3d prostoru

Podívejme se na ně postupně

Detekce příznakových bodů

Detekce příznakových bodů je rozsáhlá oblast studia, kde je již prostudováno několik algoritmů. Harrisovy algoritmy detekce rohů a Shi-Tomasiho algoritmy používají k získání dobrého příznakového bodu vlastní hodnoty. Problémem však je, že pro 3D rekonstrukci potřebujeme velké množství bodů a tyto algoritmy nám nebudou schopny poskytnout tak velký počet příznakových bodů.

Proto jako příznakové body použijeme hranové body. V další fázi algoritmu může dojít k nejednoznačnosti jejich detekce. Náš problém však vyřešíme tím, že za příznakové body vezmeme hrany. Jedním z opravdu skvělých detektorů hran je Cannyho algoritmus detekce hran. Tento algoritmus je poměrně jednoduchý a spolehlivý, pokud jde o generování hran.

Extrakce příznakových bodů

Použití epipolárního omezení skutečně zjednodušuje časovou složitost našeho algoritmu. Pro obecné problémy 3d rekonstrukce musíme pro každý bod v jednom snímku vygenerovat epipolární čáru a poté v tomto vzorkovacím prostoru vyhledat odpovídající bod v druhém snímku. Generování epipolární čáry je v našem případě také velmi snadné, jedná se pouze o iterpolaci paralelní čáry z levé roviny snímku do pravé roviny snímku.

Kontrola shody mezi snímky zahrnuje mnoho algoritmů, jako je Součet čtvercových rozdílů nebo Minimalizace energie. Aniž bychom šli příliš do hloubky, postačí našemu případu použití také použití jednoduchého Korelačního filtru.

Triangulace

Triangulace zjednodušeně řečeno je jen výpočet, kde bude ležet 3d bod pomocí dvou určených bodů v obrazových rovinách.

V realitě nelze polohu obrazových bodů přesně změřit. U obecných kamer může docházet ke geometrickým nebo fyzikálním zkreslením. Proto se za minimalizací této chyby a výpočtem co nejpřesnější 3D projekce bodů skrývá spousta matematiky. Jednoduchý model najdete na tomto odkazu.

Nápovědy

Podané jednoduché nápovědy vám pomohou vyřešit cvičení 3d_rekonstrukce. Pro toto cvičení je hojně využívána knihovna OpenCV.

Nastavení

Pomocí rozhraní API cvičení můžeme snadno získat obrázky. Po získání obrázků je také vhodné provést oboustranné filtrování obrázků, protože existují některé další detaily, které není třeba při 3d rekonstrukci zahrnout. Podívejte se na ilustrace, jak se projeví provedení oboustranného filtrování.

Výpočet korespondencí

OpenCV má již vestavěné korelační filtry, které lze volat prostřednictvím matchTemplate(). Dejte si pozor na extrémní případy, jako jsou hrany a rohy.

Jedním z dobrých postřehů je, že body vlevo budou mít korespondenci v levé části a body vpravo budou mít korespondenci v pravé části. Pomocí tohoto pozorování můžeme snadno urychlit výpočet korespondence.

Kreslení bodů

Pro triangulaci dobře funguje buď ruční, nebo funkce triangulatePoints založená na OpenCV. Jen si při provádění algebraických implementací dejte pozor na všechny tvary a velikosti matic.

Mějte na paměti rozdíl mezi jednoduchými 3D souřadnicemi a homogenními 4D souřadnicemi. Podrobnosti naleznete v tomto videu. Jednoduchým dělením úplného 4d vektoru jeho 4. souřadnicí získáme 3d souřadnice.

Vzhledem k různým implementacím uživatelů může být nutné upravit měřítko a posunutí triangulovaných bodů tak, aby byly viditelné a reprezentovatelné v grafickém rozhraní. Dobře funguje snížení měřítka 3D souřadnicového vektoru o hodnotu v rozmezí 500 až 1000. Dobře funguje také posun o 0 až 8.

Ilustrace

.