Abeliánská grupa

Posted on by admin

Stáhněte si Mathematica NotebookVYUŽIJTE TOTO TÉMA V Učebně MathWorld

Abeliánská grupa je grupa, pro kterou jsou prvky komutující (tj. AB=BA pro všechny prvky A a B). Abelovské grupy tedy odpovídají grupám se symetrickou násobicí tabulkou.

Všechny cyklické grupy jsou abelovské, ale abelovská grupa nemusí být nutně cyklická. Všechny podgrupy abelovské grupy jsou normální. V abelovské grupě je každý prvek sám o sobě v konjugační třídě a tabulka znaků zahrnuje mocniny jediného prvku známého jako generátor grupy.

V jazyce Wolfram představuje funkce AbelianGroup přímý součin cyklických grup stupňů n_1, n_2, ….

Není znám žádný obecný vzorec pro udání počtu neizomorfních konečných grup daného řádu grupy. Počet neizomorfních abelovských konečných grup a(n) libovolného daného řádu grupy n je však dán zápisem n jako

n=produkt_(i)p_i^(alfa_i),
(1)

kde p_i jsou různé prvočinitele, pak

a(n)=product_(i)P(alfa_i),
(2)

kde P(k) je rozdělovací funkce, která je ve Wolframově jazyce implementována jako FiniteAbelianGroupCount. Hodnoty a(n) pro n=1, 2, … jsou 1, 1, 1, 2, 1, 1, 1, 1, 3, 2, …. (OEIS A000688).

Nejmenší řády, pro které existují n=1, 2, 3, … neizomorfní abelovské grupy, jsou 1, 4, 8, 36, 16, 72, 32, 900, 216, 144, 64, 1800, 0, 288, 128, …. (OEIS A046056), kde 0 označuje nemožné číslo (tj. není součinem rozdělovacích čísel) neizomorfních abelovských grup. Chybějící hodnoty jsou 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41, 43, 46, …. (OEIS A046064). Přírůstkově největší čísla abelovských grup jako funkce řádu jsou 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, …. (OEIS A046054), které se vyskytují pro řády 1, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, …. (OEIS A046055).

Kroneckerova věta o rozkladu říká, že každou konečnou abelovskou grupu lze zapsat jako přímý součin cyklických grup prvočíselného řádu. Je-li grupový řád konečné grupy prvočíslo p, pak existuje jediná abelovská grupa řádu p (označujeme Z_p) a žádné neabelovské grupy. Je-li řád grupy odmocninou prvočísla p^2, pak existují dvě abelovské grupy (označené Z_(p^2) a Z_p×Z_p. Je-li řád grupy prvočíslo kubické p^3, pak existují tři abelovské grupy (označené Z_p×Z_p×Z_p, Z_p×Z_(p^2) a Z_(p^3)) a celkem pět grup. Je-li řád součinem dvou prvočísel p a q, pak existuje právě jedna abelovská grupa řádu pq (označujeme Z_p×Z_q).

Dalším zajímavým výsledkem je, že pokud a(n) označujeme počet neizomorfních abelovských grup řádu grupy n, pak

sum_(n=1)^inftya(n)n^(-s)=zeta(s)zeta(2s)zeta(3s)....,
(3)

kde zeta(s) je Riemannova zeta funkce.

Čísla abelovských grup řádů =n jsou dána 1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15, 17, 18, 19, 20, 25, …. (OEIS A063966) pro n=1, 2, …. Srinivasan (1973) také ukázal, že

suma_(n=1)^Na(n)=A_1N+A_2N^(1/2)+A_3N^(1/3)+O,
(4)

kde

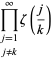A_k = produkt_(j=1; j!=k)^(infty)zeta(j/k)
(5)
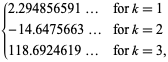= {2,294856591... pro k=1; -14,6475663... pro k=2; 118.6924619... pro k=3,
(6)

(OEIS A021002, A084892 a A084893) a zeta(s) je opět Riemannova zeta funkce. Všimněte si, že Richert (1952) nesprávně uvedl A_3=114. Součty A_k lze také zapsat v explicitních tvarech

.

.

A_1 = produkt_(j=2)^(infty)zeta(j)
(7)
A_2 = zeta(1/2)product_(j=3)^(infty)zeta(1/2j)
(8)
A_3 = zeta(1/3)zeta(2/3)product_(j=4)^(infty)zeta(1/3j).
(9)

DeKoninck a Ivic (1980) ukázali, že

suma_(n=1)^N1/(a(n))=BN+O,
(10)

kde

B = product_(p){1-sum_(k=2)^(infty)1/(p^k)}
(11)
= 0.752...
(12)

(OEIS A084911) je součin nad prvočísly p a P(n) je opět rozdělovací funkce.

Omezení počtu neizomorfních neabelovských grup uvádějí Neumann (1969) a Pyber (1993).

Existuje řada matematických vtipů týkajících se abelovských grup (Renteln a Dundes 2005):

Q: Co je fialové a komutuje? A: Abeliánský hrozen.

Q: Co je levandulové a komutuje? A: Abelianův polohrozen.

Q: Co je fialové, dojíždí a je uctíváno omezeným počtem lidí? A: Konečně uctívaný abelovský hrozen.

Q: Co je výživné a dojíždí? Odpověď: Abelova polévka.

Napsat komentář

Vaše e-mailová adresa nebude zveřejněna.