Subtrakční postup pro odstranění PL byl poprvé vypracován asi před dvaceti lety. Tento postup neovlivňuje složky EKG sousedící s frekvencí PL. Tato teoretická studie je provedena pro základní frekvenci PL, ale závěry jsou platné i pro její harmonické složky, a tedy i pro libovolný interferenční průběh. Účinnost postupu nezávisí na amplitudě rušení, pokud není zesilovač nasycen. Postup se navíc úspěšně vyrovnává se změnami amplitudy a frekvence rušení. Postup byl v průběhu let neustále zdokonalován a implementován do tisíců EKG přístrojů a počítačových systémů. Podobné přístupy publikovali i další výzkumníci .
- Principy
- Lineární kritérium
- Kompenzace amplitudových změn PL
- Lineární filtrace
- Kompenzování odchylky frekvence PL
- Vyhodnocení účinnosti postupu
- Vliv šumu EMG
- Potlačení interferencí u EKG s vysokým rozlišením
- Případ bateriově napájených přístrojů a počítačem podporovaných EKG systémů
- Automatické přizpůsobení jmenovité frekvenci PL
- Vývoj teoretického postupu
Principy
Postup odečítání se původně používá se vzorkovací frekvencí f S , která je násobkem a je hardwarově synchronizována s frekvencí PL f PL . Postup se skládá z následujících kroků :
-
EkG segmenty s frekvenčním pásmem blízkým nule jsou průběžně detekovány pomocí vhodného kritéria. Označují se jako lineární segmenty a nacházejí se především v intervalech PQ a TP, ale také v dostatečně dlouhých přímých částech vln R a T.
-
Vzorky těchto segmentů se pohyblivě průměrují, tj. podrobují se lineárnímu fázovému hřebenovému filtru s první nulou nastavenou na f PL . Takto filtrované vzorky neobsahují interferenci.
-
Amplitudy interference, nazývané korekce, se vypočítají pro každý z fázově vyrovnaných vzorků, n, v periodě PL, T PL , odečtením filtrovaných vzorků od odpovídajících vzorků kontaminovaného (původního) signálu EKG.
-
Soubor získaných korekcí se průběžně aktualizuje v lineárních úsecích a používá se v nelineárních úsecích (obvykle v okolí komplexů QRS a vln T s vysokou amplitudou) k odečtení interference od původního EKG signálu.
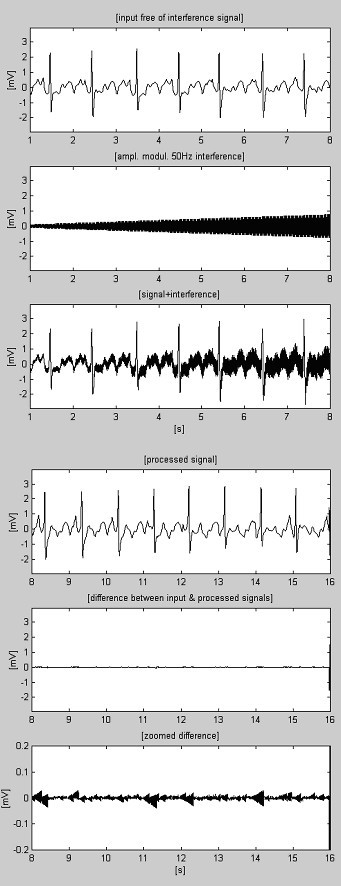
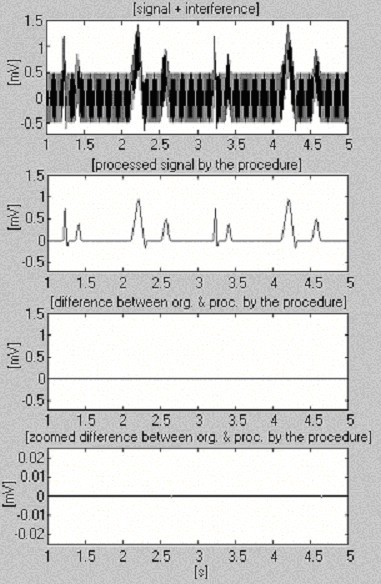
Jeden z prvních výsledků získaných metodou odečítání je uveden na obr. 1 . K čistému simulovanému EKG signálu bylo přidáno rušení, aby bylo možné vyhodnotit chyby a účinnost metody.
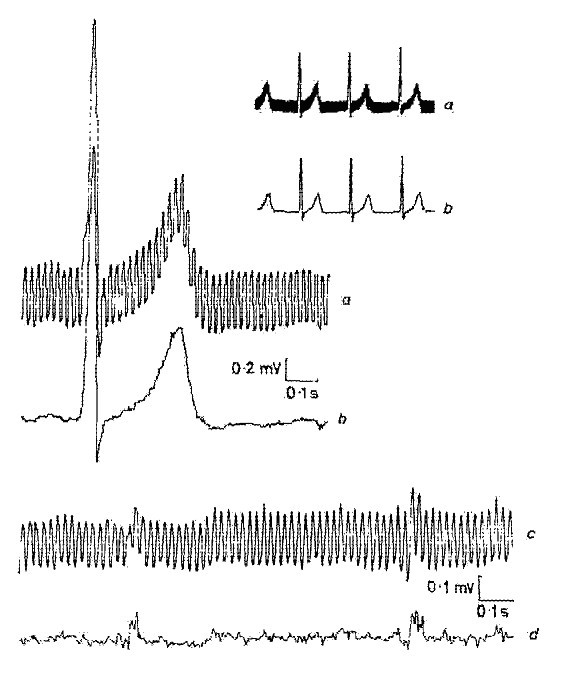
Jeden z prvních výsledků získaných postupem odečítání.
Lineární kritérium
Lineární kritérium, Cr, obvykle odpovídá druhé diferenci signálu (matematické vyhodnocení linearity). První Cr je definován následujícím způsobem. Šest po sobě jdoucích prvních diferencí, FD i , se vypočítá pomocí vzorků signálu, X i , rozmístěných po jednom T PL :
FD i = X i+n – X i , pro i = 1 … 6 (1)
Rušení PL v prvních diferencích je potlačeno, jestliže n = f S /f PL . V tomto případě je n = 5, protože postup byl původně vyvinut pro jmenovité f PL = 50 Hz a f S = 250 Hz. Dále se pro určení Cr berou maximální hodnoty FD max a minimální hodnoty FD min:
Cr = | FD max – FD min | <M, (2)
kde M je prahová hodnota.
Typické lineární a nelineární úsečky jsou znázorněny na obr. 2.
. Skutečný EKG signál (stopa a) je překryt interferencí (stopa b). Lineární segmenty zahrnují nízkofrekvenční signál a frekvenční složky siločar. Přibližné frekvenční spektrum takových lineárních segmentů je znázorněno na obr. 3.

Typické lineární a nelineární segmenty v reálném signálu EKG.
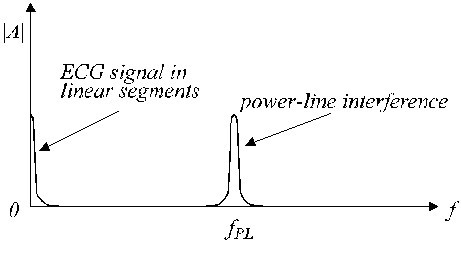
Přibližné frekvenční spektrum lineárního segmentu.
Toto kritérium funguje přesně, ale lze ho stěží použít v reálném čase, protože jeho implementace je poměrně pomalá. Tuto nevýhodu překonávají Christov a Dotsinsky, kteří používají modifikované kritérium pouhých dvou následných diferencí.
Cr = | FDi+1- FD i | <M. (3)
První vzorek, který nesplňuje rovnici (3), je spojen se začátkem úseku, který není liniový. Při přechodu z nelineárního na lineární segment by měla být rovnice (3) splněna postupně n-krát, aby nedošlo k předčasné detekci lineárního segmentu. Kritérium je realizováno v reálném čase pro f S = 400 Hz a n = 8.
Později Dotsinsky a Daskalov definovali kritérium jako dva nesouvislé rozdíly:
Cr = |FDi+k- FD i | <M, pro k >1 (4)
Tento přístup zpřesňuje přechod z lineárního na nelineární segment.
Kompenzace amplitudových změn PL
Čím častěji jsou korekce aktualizovány, tím lepší kompenzace amplitudových změn PL je dosaženo. Proto musí být práh lineárního kritéria, M, přiměřeně méně omezující, aby chyby, kterých se dopustí zprůměrování některých segmentů, které se odchylují od ideálního lineárního signálu, byly menší než chyby, které se objeví, pokud M iniciuje sporadickou aktualizaci korekce. Zpočátku byla hodnota M stanovena na 160 μV . Později byly zjištěny heuristické hodnoty M = 150 μV a M = 100 μV .
Lineární filtrace
Pro lichý počet vzorků n = 2m + 1 v jedné periodě rušení PL je filtrovaná hodnota:
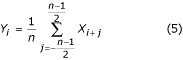
fázově shodná s nefiltrovanou.
V případě sudého čísla n = 2m jsou obě hodnoty fázově posunuty o polovinu periody vzorku:
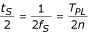
ale stanou se fázově shodnými podle vzorce
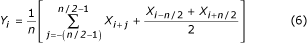
Je možné vzít pro průměrování každý druhý, třetí nebo q-tý vzorek, je-li n/q celé číslo. Podle toho, zda je n/q liché nebo sudé, se použije rovnice (7, resp. (8).

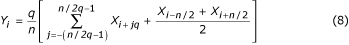
Speciální případ maximálního zmenšení vzorku vzniká při q = n/2 . Příslušný vzorec:
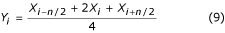
se nazývá „tříbodový“ filtr. Kromě rovnice (8) lze použít i následující vzorec
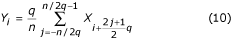
, je-li q sudé. V případě q = n/2 se filtr stává „dvoubodovým“ a je reprezentován:

Snížení počtu vzorků v periodě interference povede ke zvýšení strmosti laloků hřebenového filtru a zkrátí dobu výpočtu. Tyto „výhody“ je však třeba pečlivě posoudit, aby nedošlo k porušení Nyquistova pravidla při velkém množství přítomné třetí harmonické. Ostatní harmonické se neberou v úvahu, protože nejvyšší liché harmonické jsou obvykle potlačeny dolnopropustnými filtry s mezní hodnotou v rozmezí 100-150 Hz, zatímco sudé se vzhledem k přesné výrobě pólů generátorů elektráren prakticky nevyskytují.
Kompenzování odchylky frekvence PL
Povolená odchylka od jmenovité frekvence PL je v některých zemích omezena normami až na 1 %. V praxi je odchylka často vyšší. Kumaravel et al. uvádí pro odchylku 3 %. McManus et al. zjistili značné změny v interferenční frekvenci, která je superponována na záznamy převzaté z databáze Common Standards for Electrocardiography (CSE).
Varianty frekvence vedou ke zvláštnímu případu nevícenásobného vzorkování s reálným n, namísto celočíselného. Tuto komplikaci lze obejít, pokud se odchylky zjistí průběžným hardwarovým měřením f PL a korigují se malými úpravami vzorkovacího intervalu t S kolem jeho jmenovité (R) hodnoty, t RS = T RPL /n (zde T RPL = 20 ms je jmenovitý T PL pro f RPL = 50 Hz). Pro f PL , odchylka mezi 49,5 a 50,1 Hz, jsou odchylky t S v rozsahu 1 %, a tudíž nevnášejí chyby nad rámec přijatelné přesnosti měření parametrů, které se obvykle používají pro automatickou klasifikaci EKG.
První přístup spojuje spuštění každého prvního vzorku, S 1 , sekvence S k (k = 1, 2…n) v periodách T PL s libovolně zvolenou, ale konstantní amplitudou napětí PL. Další vzorky, S k (k = 2…n), jsou rozmístěny v intervalu t S , který se získá vztahem t S = T RTL /n. Pro frekvenci 50 Hz a n = 5 je t S = 4 ms. Dotsinsky a Daskalov studovali dva typy chyb, kterých se dopouštějí při použití tohoto přístupu. První z nich, způsobená nepravidelnostmi mezi vzorky, může dosáhnout 1 % při f S = 400 Hz a 1,2 % při f S = 250 Hz v případě 1% odchylky kolem f RPL . Druhý typ chyby nepřesahuje 3 % a je důsledkem dodatečně posunuté polohy filtrovaného vzorku.
Dotsinsky a Daskalov uvedli vylepšený přístup. Měří se probíhající perioda T PL a dělí se n. Získaný t S se použije v následném T PL .
Vyhodnocení účinnosti postupu
Příklady subtrakčního postupu jsou uvedeny na obr. 4 a obr. 5. EKG signály jsou převzaty z databáze American Heart Association. Signály jsou filtrovány vrubovou filtrací, aby se potlačilo rušení 60 Hz (frekvence PL v USA). Poté se signály smíchají s rušením 50 Hz, amplitudově modulovaným od 0 do 3,2 mVp-p rychlostí posuvu 200 μVs-1. Stopy jsou označeny takto: i) vstupní signál; ii) syntetizované rušení; iii) smíšený signál; iv) zpracovaný signál; v) rozdíl mezi původním a zpracovaným signálem a vi) zvětšený rozdíl. Vyřazené složky ve skutečnosti zahrnují také elektromyografické (EMG) a jiné šumy. V rozdílech je také přítomna nepotlačená část signálu spolu s malým zbytkovým rušením a zkreslením v důsledku kompromisu s hodnotou M.
Zpracovaný záznam AHA 3004d1.
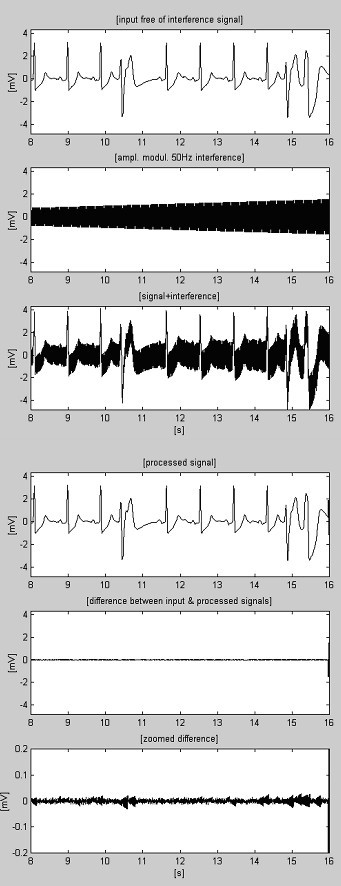
Zpracovaný záznam AHA 6007d1.
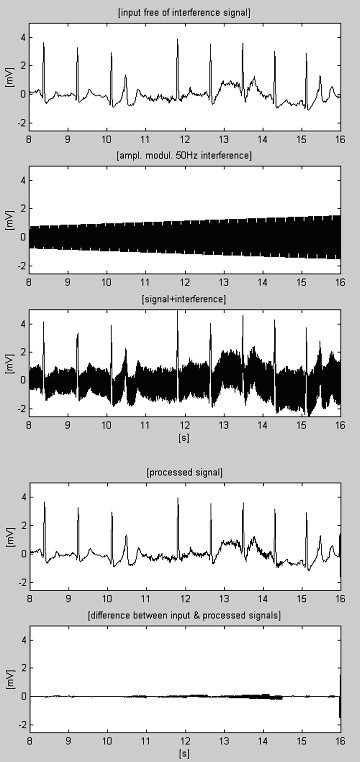
Dva signály slouží k posouzení účinnosti postupu odečítání pouze s ohledem na interferenci. První, převzatý z naší vlastní databáze, se nazývá podmíněně „čistý“ (obr. 6). Výsledek ukazuje malé rozdíly mezi vstupním a zpracovaným signálem, vizuálně způsobené šumem prezentovaným na vstupu. Tento výsledek je ověřen druhým syntetizovaným signálem, který neobsahuje žádné rušení (obr. 7). Jak je vidět, nedochází k žádnému zkreslení. Stejný syntetizovaný signál je superponován rušením a zpracován (obr. 8). Žádné zbytkové rušení nelze nalézt.
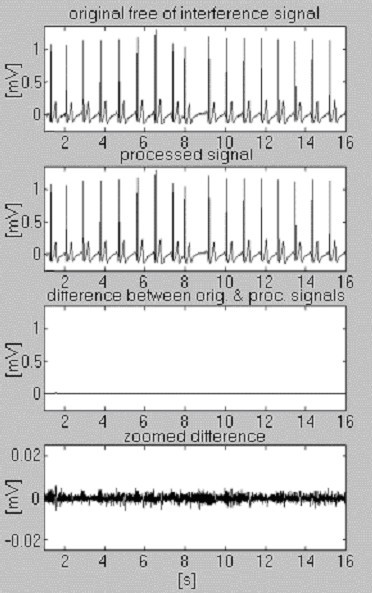
Zpracování podmíněně „čistého“ signálu.
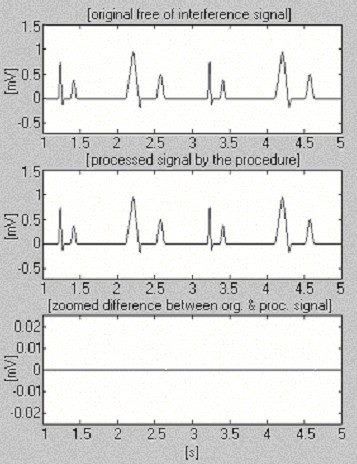
Zpracování syntetizovaného signálu.
Zpracovaný syntetizovaný signál+interference.
Vliv šumu EMG
Někdy je šum EMG tak vysoký, že ztěžuje nalezení lineárního segmentu. V důsledku toho způsobí nepřesné korekce, které neodpovídají poslední změně amplitudy interference, chyby (viz zbytkový šum mezi 11. a 14. s na obr. 9).
Zpracovaný EKG signál+EMG šum+interference.
Velmi jednoduchý přístup k potlačení vlivu EMG šumu na postup zavádí další paralelní vyrovnávací paměť, kde se probíhající části signálu bezpodmínečně průměrují . Tato vyrovnávací paměť se používá pro přesnou detekci linearity. Obr. 10 a obr. 11 ukazují srovnání výsledků bez paralelní vyrovnávací paměti a s ní. Stopy „a“ představují EKG signál smíšený s interferencí a EMG šumem. Stopy „b“ na obr. 10 a „c“ na obr. 11 ukazují přechody z lineárních do nelineárních segmentů (funkce zapnuto-vypnuto). Jak je vidět, zprůměrovaná část signálu na obr. 10 je velmi omezená. V důsledku toho se snižuje účinnost postupu (obr. 10c a 10d. Naproti tomu paralelní vyrovnávací paměť umožňuje detekci dlouhých lineárních segmentů (obr. 11c a zbytkový šum ve zpracovaném signálu (obr. 11d je nízký. Šum však není zcela potlačen, protože jeho část se podílí na korekčním výpočtu.
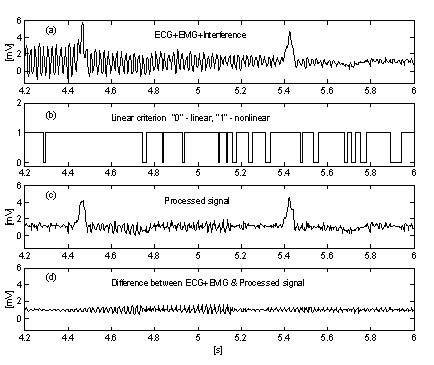
Odčítání interferenčního+EMG šumu bez paralelní vyrovnávací paměti.
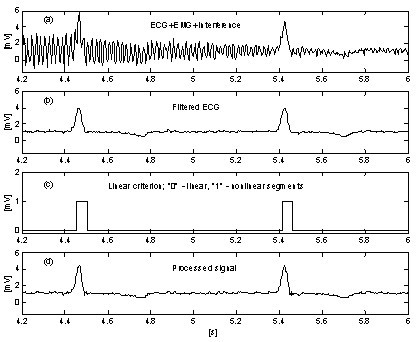
Subtrakce interferenčního+EMG šumu s paralelním bufferem.
Dalšího zlepšení potlačení šumu EMG dosáhl Christov použitím adaptivní prahové hodnoty M, která se vypočítá s ohledem na poměr šum/signál Rt, definovaný jako Rt = S NL /S F , kde úroveň šumu S NL se rovná souhrnné šířce nelineárních segmentů v epoše S F , přibližně odpovídající uvažovanému intervalu RR. Hledání linearity s kritériem M = 150 μV pro „čistý“ EKG (obr. 12a) a pro stejný signál, ale kontaminovaný šumem EMG (obr. 12b), ukazuje rozdílné S NL , (obr. 12c a 12d). Metoda je vyvinuta v prostředí MATLAB. Počáteční práh M je zvolen rovný 30 μV. Poté se postupně zvyšuje, dokud Rt nedosáhne 10 %, načež se spustí postup odečítání. Hodnota úrovně Rt ≤ 0,1 je navržena poměrem „šířka QRS versus jeho RR interval“, který se obvykle pohybuje kolem 10 %. Eliminaci interferenčního i EMG šumu lze pozorovat na obr. 13b a 13d, kde je použito M = 420 μV. Pro srovnání je „čistý“ EKG signál zpracován s M = 35 μV (obr. 13a a 13c).

Úrovně šumu SNL (stopy c a d) v „čistém“ EKG signálu (stopa a) a signálu kontaminovaném EMG (stopa b), resp.
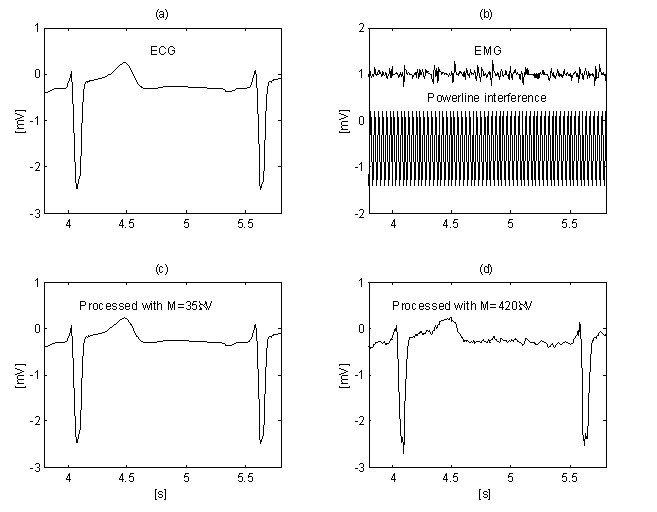
Potlačení rušení+EMG šumu pomocí adaptivního prahu M: „čistý signál“ (a) zpracovaný s M = 35 μV (c) a kontaminovaný signál (b) podrobený postupu s M = 420 μV (d).
Lineární segmenty nelze pravidelně nalézt u pacientů s fibrilací síní a komor. Pro detekci fibrilace však není nutné úplné zachování tvaru vlny, a proto lze použít všechny druhy tradičních filtrů.
Potlačení interferencí u EKG s vysokým rozlišením
Postup odečítání není přímo použitelný pro Hisův EKG na povrchu těla, protože Hisovu vlnu s nízkou amplitudou a relativně nízkou frekvencí nelze v lineárních segmentech rozlišit. Hisova vlna tak bude v praxi potlačena nebo dokonce ze signálu odstraněna. Šum EMG je obvykle vyšší amplitudy a s mnohem vyšším frekvenčním obsahem ve srovnání s povrchovou Hisovou vlnou. Proto prostá změna prahové hodnoty, M, nevede k přijatelnému vymezení lineárních a nelineárních segmentů.
Bazhina et al. zavedli následující modifikaci. Začátek detekovaného nelineárního segmentu před komplexem QRS je posunut o 100 ms doleva, čímž je oblast Hisovy vlny standardně definována jako nelineární segment (obr. 14).
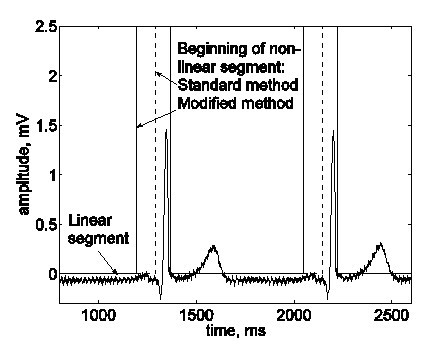
Začátek nelineárního segmentu zahrnujícího komplex QRS byl standardně posunut o 100 ms doleva, aby zahrnoval oblast, kde se očekává výskyt Hisovy vlny.
Postup odečítání a tři další metody: notch filtry, spektrální interpolace , a regresní odečítání jsou testovány proti minimálnímu zkreslení původního signálu. Jako nejlepší se ukázaly postupy odečítání a regresního odečítání, protože Baratta a kol. používají podobný koncept pro odhad šumu v lineárních segmentech. Regresně-subtrakční metoda se špatně vypořádává se změnami amplitudy rušení v rámci aktuálního segmentu.
Případ bateriově napájených přístrojů a počítačem podporovaných EKG systémů
Hardwarové měření f PL , nezbytné pro kompenzaci frekvenční modulace rušení, není u bateriově napájených přístrojů a některých počítačem podporovaných EKG systémů proveditelné. Dotsinsky a Stoyanov studovali rozsah frekvenčních změn interference s konstantní amplitudou, pro který je zbytková část omezena na přijatelnou úroveň bez použití synchronizovaného vzorkování. Zjistili, že zbytkové interference pod 20 μVp-p lze dosáhnout postupem při: i) amplitudě interference ≤ 0,4 mVp-p a ii) změně frekvence s frekvencí ≤ 0,0125 Hzs-1. Protože tyto požadavky na napájení mohou být často překročeny, bylo vyvinuto softwarové měření rušení.
Signál EKG se nejprve zpracuje pásmovým filtrem o frekvenci 49-51 Hz. Změří se amplitudy dvou sousedních vzorků, Br L a Br R , odebraných z kladného sklonu interference, které se nacházejí pod a nad nulovou čarou (obr. 15). Vzdálenost, t CP , mezi bodem křížení CP a pravým vzorkem, Br R , se vypočítá průběžně podle:
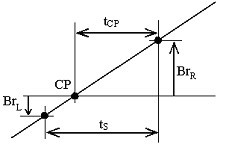
Křížení nulové linie interference.

V případě změny T PL se t S předefinuje pomocí

Tento přístup byl implementován v prostředí MATLAB. Pro vzorkovací frekvenci f S = 500 Hz a f RPL = 50 Hz je hodnota n rovna 10. Součin kn určuje dobu doporučenou k uplynutí před výpočtem a nahrazením nového tCP,i + knza předchozí tCP,i. Obr. 16 ukazuje zpracovaný 1 mV EKG signál po smíchání interferencí s konstantní amplitudou 2 mVp-p a extrémně rychle se měnící frekvencí 1 Hz za 8 s (první stopa). Pro posouzení získané účinnosti je uveden také zvětšený rozdíl bez synchronizovaného vzorkování (poslední stopa).
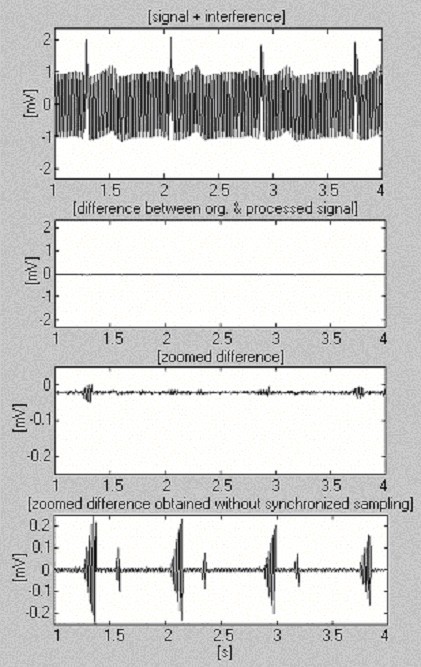
Postup subtrakce pomocí softwarového měření frekvence siločar.
Další logický krok, který je třeba provést, spočívá v: i) zachování jmenovité t S přístroje EKG, ii) převzorkování signálu podle průběžně měřeného f PL za účelem odstranění rušení a iii) návratu ke jmenovité t S . První výsledky takového přístupu jsou velmi slibné . Softwarová kompenzace proměnné f PL , stejně jako celková implementace postupu odečítání v přístroji, včetně automatického nastavení pro f RPL 50 nebo 60 Hz, bude tedy dokončena bez ohledu na hardwarové obvody a odpovídající software.
Automatické přizpůsobení jmenovité frekvenci PL
Běžný program pro alternativní odečítání rušení v prostředí 50 a 60 Hz vede k nenásobnému vzorkování, tj. k reálnému n. Široce používané hodnoty t S pro f RPL = 50 Hz, jako jsou 250, 500 a 1000 Hz, odpovídají iracionálnímu n 4,1(6), 8,3(3) a 4,1(6), pokud je třeba odstranit rušení 60 Hz. V opačném případě f S = 360 Hz vyžaduje n = 7,2. Zaokrouhlené hodnoty n* je nepřijatelné použít, protože by vnesly značnou chybu.
Velmi jednoduché řešení, které nepotřebuje změnu f S, našli Dotsinsky a Stoyanov . Původní postup používá hřebenový filtr na jedné periodě, T PL , interference. Program tedy běží rychleji. Obecně lze vzít n z k > 1 celých period. Postup je provozován, jestliže:
n = kT PL /t S je celé číslo.
Pro t S = 2 ms (f S = 500 Hz) a f RPL = 50 Hz je nejmenší hodnota k vyhovující rovnici (14) skutečně k = 1. V případě 60 Hz se však k rovná 3. Nuly spojené s dílčími harmonickými 20 a 40 Hz se objeví také, ale na postup nemají žádný vliv. Proto zcela postačí přepínat n mezi 10 (k = 1) a 25 (k = 3), aby bylo možné pracovat s oběma interferencemi. Za tímto účelem kontrolují příchozí signál dva digitální pásmové filtry. Obr. 17 ukazuje, že filtr s frekvenčním pásmem překrývajícím rušení generuje řádově vyšší výstupní signál než druhý filtr.
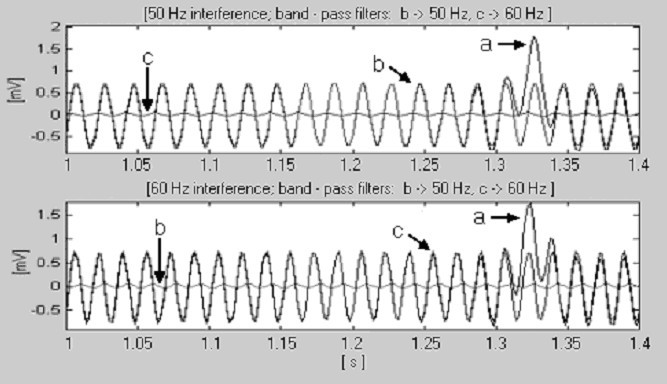
Detekce jmenovité frekvence elektrického vedení, a) část komplexu QRS, b) rušení 50 Hz a c) rušení 60 Hz.
Vývoj teoretického postupu
Teorii odečítacího postupu dále rozpracovali Mihov , Levkov a Mihov a Mihov et al. Navrhli čtyři typy filtrů, realizované v zobecněné struktuře, které mohou překonat problémy s téměř všemi případy nevícenásobného vzorkování, včetně interferenčních frekvenčních změn, bez použití synchronizované AD konverze.
Tzv. filtr D při vícenásobném vzorkování je definován jako je Cr v rovnici (2), kde druhý rozdíl, D i , je získán pomocí FD s, které jsou od sebe vzdáleny na jeden T PL :
D i = (X i+n – X i ) – (X i – X i-n ) = X i-n – 2X i + X i+n (15)
Přenosová funkce D-filtru má nuly při f = 0 a f = f PL Hz, což je znázorněno rovné 50 Hz na obr. 18.

Přenosová funkce D-filtru pro fPL = 50 Hz.
K-filtr popisuje klouzavý průměr prezentovaný rovnicemi (5 a (6). Jeho přenosová funkce je uvedena na obr. 19 pro n = 5 v případě liché násobnosti.
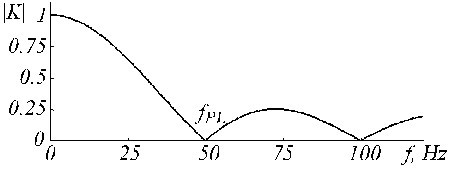
Přenosová funkce K-filtru pro fPL = 50 Hz a n = 5.
Rovnice používaná pro průběžný výpočet rušivých složek:
B i = X i – Y i (16)
ve skutečnosti definuje digitální filtr nazývaný (1-K)-filtr.
Dále jsou filtry nově definovány pro nevícenásobné vzorkování a pro ilustraci softwarového zlepšení se bere v úvahu f S = 250 Hz ve spojení s f RPL = 60 Hz.
Aby se zachovaly nuly přenosové funkce, musí se D-filtr odečíst korekčním filtrem s nulou při f = 0 a ziskem D RPL při f = f RPL , který se rovná zisku D-filtru pro stejnou frekvenci, f RPL . Syntéza korekčního filtru je založena na tříbodovém pomocném filtru daném rovnicí:

kde (n/2)* je zaokrouhlená hodnota n/2.
Protože A RPL je zisk pomocného filtru pro f = f RPL , korekční filtr se vynásobí poměrem D RPL /A RPL . Pomocí odpovídajících přenosových funkcí se D RPL a A RPL předem vypočtou:
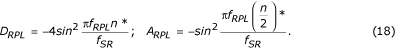
Konec se opravený D*-filtr představí jako

a je znázorněn na obr. 20 stopou „c“, kde stopy „a“ a „b“ jsou D-filtr, resp. korekční filtr.
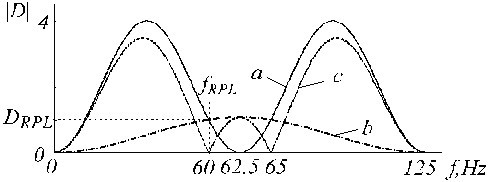
Přenosové funkce a) D-filtru, b) pomocného korekčního filtru a c) korigovaného D-filtru.
Přenosová funkce K-filtru musí zachovávat nulu pro f = f RPL , jednotkový zisk pro f = 0 a lineární fázovou charakteristiku. Postup korekce K-filtru je podobný předchozímu. Pomocný filtr je dán vzorcem používaným pro výpočet korekcí:
A i = X i – Y i , (20)
Zisk filtru je roven 1 – K RPL pro f = f RPL , kde K RPL je zisk K-filtru pro stejnou frekvenci f RPL . Pomocný filtr se vynásobí K RPL /(1 – K RPL ) a odečte se od K-filtru. Rovnice pro korigovaný K*-filtr je:
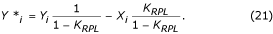
Konstantu K RPL lze odhadnout podle:

pro lichou, resp. sudou násobnost.
Příklad korekce filtru K je znázorněn na obr. 21, kde stopy „a“, „b“ a „c“ představují primární filtr K, pomocný filtr a korigovaný filtr K*.
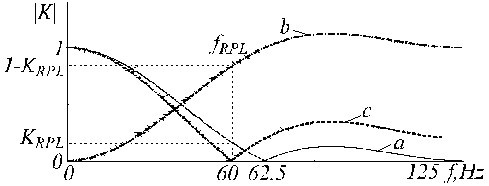
Přenosová funkce a) K-filtru, b) pomocného korekčního filtru a c) opraveného K-filtru.
V případě nevícenásobného vzorkování vzniká fázový rozdíl mezi probíhajícími vzorky EKG a rušivými složkami B i (rovnice 16), které se obvykle nacházejí v dočasné vyrovnávací paměti FIFO (first-in-first-out). Proto se B i musí upravit a odečíst od vzorků EKG během nelineárních segmentů. Postup kompenzace je poměrně složitý. Obr. 22 ukazuje obsah dočasné vyrovnávací paměti. Aktuální rušivý vzorek, B i-n *, se neshoduje s obnoveným vzorkem, B i . Jeho amplituda se musí přepočítat, aby se vyrovnal jejich fázový rozdíl. Toho se dosáhne pomocí nového filtru s lineární fázovou charakteristikou a jednotkovým zesílením pro f = f RPL , označovaného jako B-filtr. Syntetizuje se ze známého K-filtru s oknem rovným interferenční periodě. V případě lichého n* jej lze popsat takto:
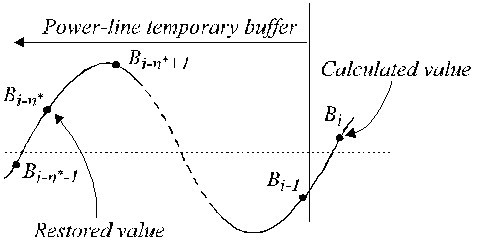
Obnovené hodnoty v dočasné vyrovnávací paměti.
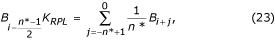
kde K RPL je zesílení pro rušení filtru průměrování dané rovnicí (22).
Obnovenou hodnotu vyrovnávací paměti B i lze vypočítat podle:
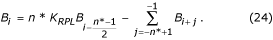
V případě sudého n*:
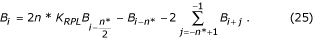
Přenosová funkce filtru B je znázorněna na obr. 1. 23.
Přenosové funkce a) B-filtru a b) známého K-filtru.
Zobecněná struktura je uvedena na obr. 23. 24, kde jsou moduly postupu odečítání následující:
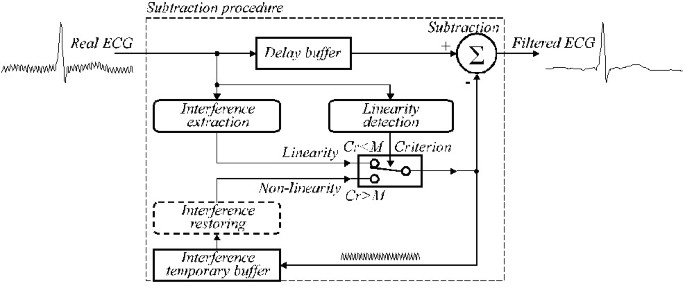
Zobecněná struktura postupu odečítání.
-
Detekce linearity. K vyhodnocení linearity každého sousedství vzorku signálu se použije D-filtr.
-
Vylučování rušení. (1-K)-filtr se používá k výpočtu rušivé složky.
-
Kritérium. Podmínka Cr <M posílá buď extrahované, nebo obnovené PL rušení do Subtraction.
-
Interference temporary buffer. Extrahovaná nebo obnovená složka rušení použitá jako korekce v nelineárním segmentu je uložena na pozici uzamčené s probíhající fází silnoproudého rušení.
-
Obnovení rušení. B-filtr se volá v případě nevícenásobného vzorkování, aby se obnovily skutečné hodnoty korekce, které se musí odečíst od vzorků vstupního signálu v nelineárních segmentech.
-
Zpožďovací vyrovnávací paměť. Vyrovnává zpoždění, které se objevuje u D-filtru a (1-K)-filtru a je nezbytné, pokud procedura probíhá v kvazireálném čase. V opačném případě by se vyrovnávací paměť mohla zanedbat.
-
Subtrakce. Extrahovaná nebo obnovená hodnota rušení se odečte od zpožděného vstupního signálu, aby byl na výstupu „čistý“ EKG signál. V případě nelinearity jak extrakce interference, tak odečítání implementují K-filtr.
Vylepšený algoritmus podle zobecněné struktury byl testován off-line. Výsledky pro f S = 250 Hz a f RPL = 60 Hz jsou uvedeny na obr. 25.
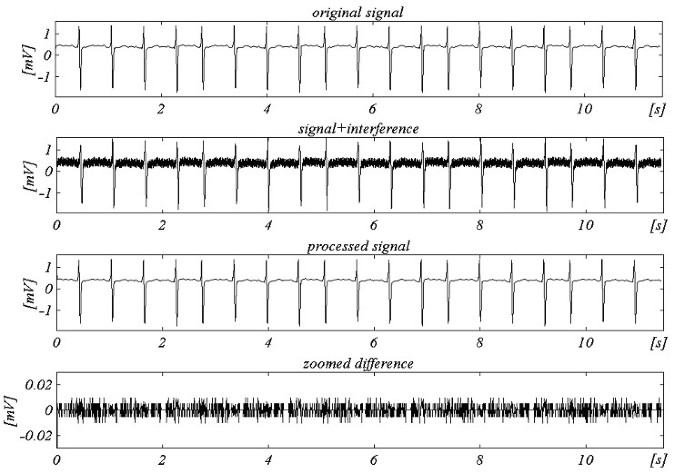
Příklad pro nevícenásobné vzorkování s fRPL = 60 Hz a fS = 250 Hz.
.