Podívejte se na poslední články

Abstrakt

Světlo se ve vakuu šíří rychlostí c bez ohledu na pohyb zdroje světla nebo vztažné soustavy pozorovatele. V důsledku toho je k cestě světla od zdroje světla k pozorovateli v prostoru zapotřebí určitý čas, takže vyzařování světla a pozorování vyzařovaného světla nejsou současné. Na základě těchto úvah je navržena metoda měření absolutní rychlosti pozorovatele, která by mohla být použita k určení stavu pohybu kosmické lodi uvnitř uzavřené kabiny. In this study, a new explanation of the Lorentz transformation is also introduced.

Klíčová slova

souřadnicový systém, vztažný systém, pohyb, absolutní rychlost, relativita, Lorentzova transformace, čas, prostor, pozorovatel, zdroj světla
Následující analýza představuje praktický postup měření absolutní rychlosti pozorovatele, který by mohl být použit pro určení pohybového stavu kosmické lodi z vnitřku uzavřené kabiny. Pojem absolutní rychlost obecně označuje standardní jednotnou rychlost různých objektů fyzikální soustavy vzhledem k postulovanému nehybnému prostoru, který existuje nezávisle na fyzikálních objektech v něm obsažených (tj. absolutní prostor). V tomto článku představujeme přístup založený na rigidní kinematice, který ukazuje, že absolutní rychlost pozorovatele lze určit ze skutečnosti, že světlo se pohybuje vakuem rychlostí c bez ohledu na pohyb zdroje světla nebo na pohyb vztažné soustavy pozorovatele. V důsledku toho je k cestě světla od zdroje světla k pozorovateli v prostoru zapotřebí určitý čas, takže vyzařování světla a pozorování vyzařovaného světla nejsou současné.
V navrhované analýze nejprve uvedeme následující konvence pro uvažované souřadnicové systémy. Předpokládáme kartézský souřadnicový systém tvořený třemi na sebe kolmými osami vycházejícími z bodu (0,0,0), kde libovolný bod P v prostoru lze definovat jeho souřadnicemi podél os x, y a z, reprezentovanými uspořádanou dvojicí reálných čísel (x,y,z). Předpokládá se, že inerciální vztažný systém S je reprezentován prostorovým pravoúhlým souřadnicovým systémem (x,y,z), jehož počátek je O. Řada standardních hodin (označovaných jako hodiny S) je umístěna ve stacionárních bodech v S. Hodiny S jsou vzájemně kalibrovány (tj. poskytují ekvivalentní údaje ve stejném časovém okamžiku) na základě vysílání a příjmu světelného signálu. Konkrétně v čase tA je světelný paprsek promítnut z hodin A na hodiny B, který se pak v čase tB od hodin B odrazí zpět k hodinám A a v čase tA‘ dorazí do hodin A. Pokud , jsou obě hodiny kalibrovány. Pro libovolnou událost umístěnou na souřadnicích x,y,z je její časová souřadnice t dána údajem hodin S souvisejících s událostí. Podobně je vytvořen další inerciální vztažný systém S‘ založený na druhém prostorovém pravoúhlém souřadnicovém systému (x‘,y‘,z‘), jehož počátek je O‘, a další řada vzájemně kalibrovaných standardních hodin (hodin S‘) je umístěna ve stacionárních bodech vztažného systému S‘. Pro jakoukoli událost umístěnou na souřadnicích x‘,y‘,z‘ je její časová souřadnice t‘ dána údajem hodin S‘ souvisejících s událostí.
Protože příslušné počátky prostorových a časových souřadnic, jakož i směry souřadnicových os lze do značné míry volit libovolně, vztahy mezi S a S‘ použité v tomto dokumentu jsou založeny na následujících konvencích, které byly použity pro zjednodušení.
(1) V určitém časovém okamžiku jsou počátky a souřadnicové osy obou systémů superponovány a hodiny umístěné v O a O‘ jsou nastaveny na nulu, tj, .
(2) Osy x a x‘ jsou ve směru relativního pohybu S a S‘ shodné; x a x‘ jsou tedy vždy shodné, zatímco y a y‘, stejně jako z a z‘ jsou rovnoběžné.
(3) S‘ se pohybuje ve směru +x S.
Navržená analýza vychází ze základního principu, že světlo se ve vakuu pohybuje konstantní rychlostí c bez ohledu na pohyb pozorovatele nebo zdroje světla. Proto zde definujeme absolutní rychlost U pozorovatele, o níž předpokládáme, že je lineární a rovnoměrná, jako , kde f(φ) představuje funkci geometrického vztahu mezi směrem světelného signálu a směrem U, který zde označujeme jako φ.
V navrhované analýze jsou uvedena dvě nová vysvětlení relativity času a délky, která se liší od Einsteinových vysvětlení (viz „O elektrodynamice pohybujících se těles“). Tato vysvětlení jsou uvedena v následujících oddílech.

Relativita času

Vzhledem ke konečné rychlosti světla je k cestě světla od zdroje světla k pozorovateli v prostoru zapotřebí určitý čas. Z toho lze odvodit, že vyzařování světla a pozorování světla nemohou probíhat současně. Na základě stálosti rychlosti světla a podmínek znázorněných na obrázku 1 definujeme následující faktory. Polohy zdroje světla a pozorovatele v okamžiku , kdy zdroj světla emituje světlo (označujeme jako událost R), jsou dány jako A a H0. Během doby šíření světla z do urazí pozorovatel vzdálenost U∙T z polohy H0 do H, načež pozorovatel přijme emitované světlo. V souladu s tím definujeme jako vzdálenost l mezi polohou pozorovatele při příjmu světelného signálu v bodě a polohou světelného zdroje při vyzařování světla v bodě . Vzhledem ke stálosti rychlosti světla je . Vzdálenost je ekvivalentní U∙T. Konečně definujeme jako vzdálenost l0 mezi polohou pozorovatele v bodě a polohou zdroje světla v bodě . Zde zavádíme úvahu o poloze pozorovatele v bodě , o níž se dříve soudilo, že nemá žádný fyzikální význam. Jsou-li pohybové stavy pozorovatele a zdroje světla ekvivalentní, je dáno l0, takže U lze vypočítat pomocí trojúhelníkových vztahů znázorněných na ,obrázku 1.
V této práci se čas události měří následující metodou. Pozorovatel i hodiny jsou umístěny v počátku. Když světelný signál představující výskyt události dorazí k pozorovateli, bude čas příchodu světla odpovídat času indikovanému hodinami. Výhodou této shody je, že se vždy vztahuje k poloze pozorovatele, který hodiny používá. Jak je vidět na obrázku 1, prostorový bod O3 lze definovat na základě polohy světelného zdroje při vyzařování světla v bodě a prostorový bod O2 lze definovat na základě polohy pozorovatele při příjmu světla v bodě . Způsob definování prostorového bodu O1, v němž se nachází pozorovatel, když světelný zdroj vyzařuje světlo při , však není zřejmý. K řešení tohoto problému se zavádějí pojmy absolutní klid (tj. ) a absolutní pohyb (tj. ). Jediného pohybujícího se pozorovatele v bodě H0, respektive H nahradíme dvěma pozorovateli H1 a H2 v klidu v prostorových bodech O1, respektive O2, zatímco zdroj světla A je v klidu v prostorovém bodě O3. Každý z pozorovatelů a zdroj světla používají kalibrované standardní hodiny a A vysílá světelný signál v čase , který označujeme jako událost R0. Když pozorovatel H1 přijme světelný signál pohybující se rychlostí c, údaj hodin je T0, a když jej přijme H2, údaj je T. Vzdálenosti a lze tedy definovat na základě příslušných dob pohybu světelného signálu takto:
, (1)
a
. (2)
Podle trojúhelníkových vztahů znázorněných na obrázku 1 je transformace události R0 mezi pozorovateli H1 a H2 dána takto:
(3)
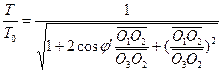(4)
Zde je úhel mezi přímkou O3O1 a osou x a je úhel mezi přímkou O3O2 a osou x.
Vrátíme-li se nyní k podmínce jediného pohybujícího se pozorovatele, předpokládáme, že v soustavě S pozorovatel H i zdroj světla A používají kalibrované standardní hodiny. V okamžiku události R se zdroj světla A nachází v prostorovém bodě O3 a pozorovatel H v bodě O1. Okamžiku, kdy světelný signál dosáhne prostorového bodu O1, odpovídá údaj hodin S T0. V okamžiku, kdy pozorovatel H obdrží světelný signál, je údaj T a H se nachází v bodě O2.
H samozřejmě nemůže pozorovat událost R v bodě O1. K vyřešení tohoto problému je v soustavě S umístěn další pozorovatel H- v bodě O1 odpovídajícím , přičemž poloha H- je použita k určení prostorového bodu O1. Pak lze transformaci události R mezi pozorovateli H- a H získat pomocí rovnice (3) takto.
(5)
Z toho vyplývá, že rovnice (3) a (4) lze přepsat takto:
(6)
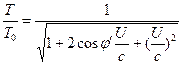(7)
e si také všimněte, že pro se rovnice (6) a (7) zjednodušují na následující.
(8)
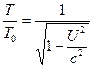(9)
Na základě výše uvedené analýzy lze tedy z rovnice (6) získat jednoduchou metodu pro určení U za předpokladu, že je známa (φ).
Pro zjednodušení je jako vztažná soustava zvolen zdroj světla s ekvivalentním pohybovým stavem, jaký mají pozorovatelé. Pozorovatel je umístěn ve středu rovné tuhé tyče v rovnoměrném lineárním pohybu a světelné signály z různých míst na tyči přicházejí k pozorovateli v různých časech. Pozorovatel detekuje výchylku tyče v poloze pozorovatele s úhlem výchylky , který lze získat z rovnice (8).
Pomocí této metody by bylo možné určit stav pohybu kosmické lodi z uzavřené kabiny.

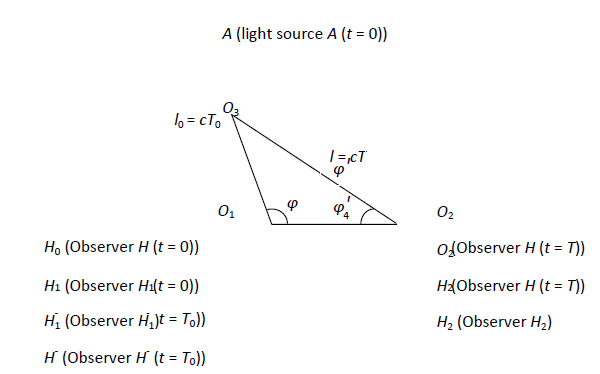
Obrázek 1: stavy pohybu pozorovatele a zdroje světla

Relativita délky

Ve výše uvedené analýze byly zavedeny dvě délky, tj. V tomto případě uvažujeme délku tyče, o níž se předpokládá, že je to nehybná tuhá tyč délky L v rámci své souřadnicové soustavy, pro kterou se L měří nehybným tyčovým měřidlem a kde osa tyče je shodná s osou x souřadnicové soustavy, která se pohybuje rovnoměrným lineárním pohybem podél směru +x absolutní rychlostí U. Předpokládá se, že L je určena dvěma níže definovanými operacemi.
(a) Pozorovatel se nachází ve stejné pohyblivé souřadnicové soustavě jako tyč a tyčové měřidlo a L se měří superpozicí tyčového a tyčového měřidla.
(b) Pomocí několika hodin umístěných ve stacionárních souřadnicích, které se pohybují synchronizovaně, změří pozorovatel polohy obou konců tyče ve stacionárních souřadnicích v určitém okamžiku t a vzdálenost mezi oběma polohami se změří pomocí stacionárního tyčového měřidla. je délka vypočtená z operace (a), která se zde označuje jako délka tyče v pohyblivých souřadnicích. je délka vypočtená z operace (b), která je zde označena jako délka pohyblivé tyče ve stacionární souřadnici. Je zřejmé, že a se liší.
Předpokládáme, že v soustavě S je pozorovatel H- ve stejném pohybovém stavu jako H. Pak, jak je znázorněno na obr. 1, se H- při příjmu světelného signálu v bodě nachází v bodě O1 a současně pozorovatel H v bodě O4. Proto je t=0,04
vzdálenost mezi H- a H v bodě a
. (10)
je vzdálenost, kterou urazil pozorovatel H v intervalu od T0 do T tak, že
. (11)
je vzdálenost mezi H- v bodě a H v bodě taková, že
. (12)
Z toho lze odvodit následující výraz:
(13)
Následující úvahy se budou týkat souřadnicových a časových transformací mezi dvěma pohybujícími se souřadnicovými systémy, které se oba pohybují rovnoměrnou lineární rychlostí, což představuje nové vysvětlení Lorentzovy transformace.
Předpokládáme, že pozorovatel H (v soustavě S), pozorovatel H‘ (v soustavě S‘) a světelný zdroj A“ (v soustavě S“) používají individuálně kalibrované standardní hodiny a v okamžiku světelný zdroj A“ vyšle světelný signál, označený jako událost R“. V okamžiku události R“ se zdroj A“ nachází v bodě O3 a pozorovatelé H a H‘ se shodují. V okamžiku, kdy pozorovatel H přijme světelný signál, je údaj hodin S roven T a H se nachází v bodě O1. Když pozorovatel H‘ přijme světelný signál, údaj hodin S‘ je T‘ a H‘ je v bodě O2. Pak lze transformaci události R“ mezi pozorovateli H‘ a H vypočítat z rovnice (3), kde
. (14)
Zde u je relativní rychlost mezi pozorovateli H‘ a H, která dává následující transformace.
(15)
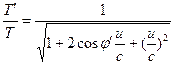(16)
Z lze odvodit následující vztahy:
. (17)
Při a se rovnice (16) zjednoduší na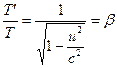
. (18)
Z toho lze odvodit následující transformační vztahy:
, (19)
, (20)
, (21)
. (22)
Mimo to, když ,
, (23)
a
, (24)
, (25)
, (26)
. (27)