Toleranční intervaly
Tato část obsahuje statistické údaje pro jednostranné a oboustranné toleranční intervaly.
Intervaly založené na normálním rozdělení
Jednostranný interval
Jednostranný interval se vypočítá následujícím způsobem:
Dolní mez = 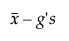
Horní mez = 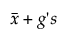
kde
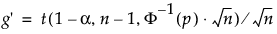
s je směrodatná odchylka
t je kvantil od ne.centrálního t-rozdělení
Φ-1 je standardní normální kvantil
Dvoustranný interval
Dvoustranný interval se vypočítá takto:
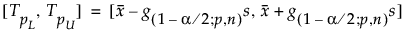
kde s je směrodatná odchylka a g(1-α/2; p,n) je konstanta.
Pro určení g uvažujte podíl populace, který je zachycen v tolerančním intervalu. Tamhane a Dunlop (2000) uvádějí tento podíl takto:
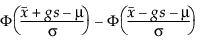
kde Φ označuje standardní normální cdf (kumulativní distribuční funkci).
Tedy g řeší následující rovnici:
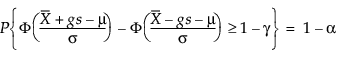
kde 1 – γ je podíl všech budoucích pozorování obsažených v tolerančním intervalu.
Další informace o tolerančních intervalech založených na normálním rozdělení viz tabulky J.1.a, J.1b, J.6a a J.6b v Meeker et al. (2017).
Neparametrické intervaly
Jednostranná dolní mez
Dolní 100(1 – α)% jednostranná toleranční mez, která má obsahovat alespoň podíl β výběrového rozdělení ze vzorku o velikosti n, je řádová statistika x(l). Index l se vypočítá takto:
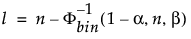
kde Φ-1bin(1-α, n, β) je (1 – α)-tý kvantil binomického rozdělení s n pokusy a pravděpodobností úspěchu β.
Skutečná hladina spolehlivosti se vypočítá jako Φbin(n-l, n, β), kde Φbin(x, n, β) je pravděpodobnost, že binomicky rozdělená náhodná veličina s n pokusy a pravděpodobností úspěchu β je menší nebo rovna x.
Poznamenejme, že pro výpočet dolního jednostranného tolerančního intervalu bez rozdělení musí být velikost vzorku n alespoň tak velká jako 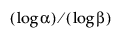 .
.
Jednostranná horní mez
Horní 100(1 – α)% jednostranná toleranční mez, která má obsahovat alespoň podíl β výběrového rozdělení ze vzorku o velikosti n, je řádová statistika x(u). Index u se vypočítá takto:
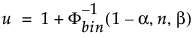
kde Φ-1bin(1-α, n, β) je (1 – α)-tý kvantil binomického rozdělení s n pokusy a pravděpodobností úspěchu β.
Skutečná hladina spolehlivosti se vypočítá jako Φbin(u-1, n, β), kde Φbin(x, n, β) je pravděpodobnost, že binomicky rozdělená náhodná veličina s n pokusy a pravděpodobností úspěchu β je menší nebo rovna x.
Všimněte si, že pro výpočet horního jednostranného tolerančního intervalu bez rozdělení musí být velikost vzorku n alespoň tak velká jako 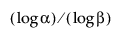 .
.
Dvoustranný interval
Dvoustranný toleranční interval 100(1 – α)%, který má obsahovat alespoň podíl β výběrového rozdělení ze vzorku velikosti n, se vypočítá takto:
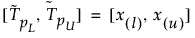
kde x(i) je statistika i-tého řádu a l a u se počítají takto:
Nechť ν = n – Φ-1bin(1-α, n, β), kde Φ-1bin(1-α, n, β) je (1 – α)kvantil binomického rozdělení s n pokusy a pravděpodobností úspěchu β. Je-li ν menší než 2, nelze vypočítat toleranční interval bez oboustranného rozdělení. Je-li ν větší nebo rovno 2, l = floor(ν/2) a u = floor(n + 1 – ν/2).
Skutečná hladina spolehlivosti se vypočítá jako Φbin(u-l-1, n, β), kde Φbin(x, n, β) je pravděpodobnost binomicky rozdělené náhodné veličiny s n pokusy a pravděpodobností úspěchu β menší nebo rovna x.
Poznamenejme, že pro výpočet oboustranného tolerančního intervalu bez rozdělení musí být velikost vzorku n alespoň tak velká jako n v následující rovnici:

Další informace o tolerančních intervalech bez rozdělení viz Meeker et al. (2017, odd. 5.3).
.