Den tredje lov postulerer, at entropien i et stof altid er endelig, og at den nærmer sig en konstant, når temperaturen nærmer sig nul. Værdien af denne konstant er uafhængig af værdierne af alle andre tilstandsfunktioner, der karakteriserer stoffet. For ethvert givet stof kan vi frit tildele en vilkårligt valgt værdi til grænseværdien ved nul-temperaturen. Vi kan imidlertid ikke tildele alle stoffer vilkårlige nul-temperatur-entropier til alle stoffer. Det sæt af tildelinger, vi foretager, skal være i overensstemmelse med de eksperimentelt observerede nul-temperaturgrænseværdier for entropiændringer ved reaktioner mellem forskellige stoffer. For perfekt krystallinske stoffer er disse reaktionsentropier alle nul. Vi kan opfylde denne betingelse ved at tildele en vilkårlig værdi til den molære nul-temperaturentropi for hvert grundstof og fastsætte, at nul-temperaturentropien for enhver forbindelse er summen af nul-temperaturentropierne for de elementer, der indgår i den. Denne beregning er meget forenklet, hvis vi lader nul-temperaturentropien for hvert grundstof være nul. Dette er det væsentlige indhold af den tredje lov.
Lewis og Randalls erklæring inkorporerer dette valg af nul-entropi-referencetilstanden for entropier, idet den specificerer den som “en krystallinsk tilstand” for hvert grundstof ved nul grader. Som følge heraf er entropien for ethvert stof ved nul grader større end eller lig med nul. Det vil sige, at Lewis og Randalls erklæring indeholder en konvention, der fastsætter grænseværdien for ethvert stofs entropi ved nul-temperatur. I denne henseende er Lewis og Randalls erklæring et i det væsentlige arbitrært valg, som ikke er en iboende egenskab i naturen. Vi ser imidlertid, at det er et overvældende bekvemt valg.
Vi har diskuteret alternative udsagn af den første og anden lov. En række alternative udsagn af den tredje lov er også mulige. Vi overvejer følgende:
Det er umuligt at opnå en temperatur på det absolutte nulpunkt.
Dette udsagn er mere generelt end Lewis og Randalls udsagn. Hvis vi overvejer at anvende dette udsagn på de temperaturer, der kan opnås i processer, der involverer et enkelt stof, kan vi vise, at det implicerer og er impliceret af Lewis og Randall udsagnet.
Varmekapacitetens egenskaber, \(C_P\), spiller en central rolle i disse argumenter. Vi har set, at \(C_P\) er en funktion af temperaturen. Selv om det ikke er nyttigt at gøre det, kan vi anvende den definerende relation for \(C_P\) på et stof, der gennemgår en faseovergang, og finde \(C_P=\infty\). Hvis vi tænker på et stof, hvis varmekapacitet er mindre end nul, støder vi på en modsigelse af vores grundlæggende ideer om varme og temperatur: Hvis \(q>0\) og \({q}/{\Delta T}<0\), må vi have \(\Delta T<0\); det vil sige, at opvarmning af stoffet får dets temperatur til at falde. Kort sagt, den teori, vi har udviklet, indlejrer forudsætninger, der kræver \(C_P>0\) for ethvert system, som vi kan foretage målinger på.
Lad os karakterisere et system med rent stof ved dets tryk og temperatur og overveje reversible processer med konstant tryk, hvor kun tryk-volumen arbejde er muligt. Så er \({{\left({\partiel S}/{\partiel T}\right)}_P={C_P}/{T}\) og \(dS={C_PdT}/{T}\). Vi vil nu vise: Lewis og Randalls bestemmelse om, at entropien altid er endelig, kræver, at varmekapaciteten går til nul, når temperaturen går til nul. (Da vi skal vise, at den tredje lov forbyder målinger ved det absolutte nulpunkt, er denne konklusion i overensstemmelse med vores konklusion i det foregående afsnit). At varmekapaciteten går til nul, når temperaturen går til nul, fremgår af \(S={C_PdT}/{T}.\) Hvis \(C_P\) ikke går til nul, når temperaturen går til nul, bliver \(dS\) vilkårligt stor, når temperaturen går til nul, hvilket er i modstrid med Lewis og Randalls udsagn.
For at udvikle dette resultat mere eksplicit lader vi varmekapaciteterne ved temperaturerne \(T\) og nul være henholdsvis \(C_P\left(T\right)\) og \(C_P\left(0\right)\). Da \(C_P\left(T\right)>0\) for enhver \(T\ >0\), har vi \(S\left(T\right)-S\left(T^*\right)>0\) for enhver \(T>T^*>0\). Da entropien altid er endelig, \(\infty >S\left(T\right)-S\left(T^*\right)>0\), således at
\\\ }>0\]
og
\
for temperaturer i nabolaget af nul, kan vi udvide varmekapaciteten med vilkårlig nøjagtighed som et Taylor-polynomium i \(T\):
Ulighederne bliver
Den venstre betingelse kræver \(C_P\left(0\right)=0\).
Vi kan se den tredje lov som et udsagn om varmekapaciteterne for rene stoffer. Vi udleder ikke kun, at \(C_P>0\) for alle \(T>0\), men også, at
\
Mere generelt kan vi udlede tilsvarende påstande for lukkede reversible systemer, der ikke er rene stoffer: \({{{\left({\partial H}/{\partial T}\right)}_P>0\) for alle \(T>0\), og \({{\mathop{\mathrm{lim}}}_{T\til 0} T^{-1}{{\left({\partial H}/{\partial T}\right)}_P=0}\ }\). (Nul-temperatur-entropierne i sådanne systemer er dog ikke nul.) I diskussionen nedenfor beskriver vi systemet som et rent stof. Vi kan i det væsentlige føre de samme argumenter for ethvert system; vi behøver blot at erstatte \(C_P\) med \({{\left({\partiel H}/{\partiel T}\right)}_P\). Lewis og Randalls udsagn hævder, at entropien bliver konstant ved det absolutte nulpunkt, uanset værdierne af alle andre termodynamiske funktioner. Det følger heraf, at entropien ved nul grader er uafhængig af værdien af trykket. For to vilkårlige tryk, \(P_1\) og \(P_2\), har vi \(S\left(P_2,0\right)-S\left(P_1,0\right)=0\). Hvis vi lader \({P=P}_1\) og \(P_2=P+\Delta P\) og , har vi
\
for enhver \(\Delta P\). Derfor har vi
\
I kapitel 10 finder vi \({{\left({\partiel S}/{\partiel }P\right)}_T=-{\left({\partiel V}/{\partiel T}\right)}_P\), så både entropien og volumenet nærmer sig deres nul-temperaturværdier asymptotisk.
Når vi siger, at det absolutte nulpunkt er uopnåeligt, mener vi, at intet system kan undergå nogen ændring, hvor dets sluttemperatur er nul. For at se, hvorfor det absolutte nulpunkt må være uopnåeligt, skal vi overveje processer, der kan sænke temperaturen i et system. Generelt har vi varmebeholdere til rådighed ved forskellige temperaturer. Vi kan vælge det tilgængelige reservoir, hvis temperatur er lavest, og bringe systemet til denne temperatur ved simpel termisk kontakt. Så meget er trivielt; det er klart, at udfordringen er at sænke temperaturen yderligere. For at gøre det må vi foretage en anden ændring. Uanset hvad denne ændring måtte være, kan den ikke fremmes af en udveksling af varme med omgivelserne. Når vi først har bragt systemet ned på temperaturen i den koldeste tilgængelige del af omgivelserne, kan enhver yderligere udveksling af varme med omgivelserne kun være kontraproduktiv. Vi konkluderer, at enhver proces, der er egnet til vores formål, må være adiabatisk. Da en adiabatisk proces ikke udveksler nogen varme med omgivelserne, er \(\Delta \hat{S}=0\).
Processen må også være en mulig proces, således at \(\(\Delta S+\Delta \hat{S}\ge 0\), og da den er adiabatisk, er \(\(\Delta S\ge 0\). Lad os betragte en reversibel proces og en irreversibel proces, hvor det samme system\({}^{2}\) går fra den tilstand, der er angivet ved \(P_1\) og \(T_1\), til en anden tilstand, hvor trykket er \(P_2\). De endelige temperaturer og entropiforandringer i disse processer er forskellige. For den reversible proces er \(\(\Delta S=0\); vi betegner den endelige temperatur som \(T_2\). For den irreversible proces er \(\(\Delta S>0\); vi betegner den endelige temperatur som \(T^*_2\). Det viser sig, at temperaturændringen er mindre for den irreversible proces end for den reversible proces; det vil sige \(T_2-T_1<t^*_2-t_1\)>. Den reversible proces opnår således en lavere temperatur: \({T_2<t}^*_2\)>. Ud fra
\
kan vi beregne entropiændringerne for disse processer. For den reversible proces beregner vi \
Dertil beregner vi først
for den isoterme reversible omdannelse fra tilstanden \(P_1\), \(T_1\) til den tilstand, der er angivet ved \(P_2\) og \(T_1\). For dette trin er \(dT\) nul, og derfor
Vi beregner derefter
for den isobare reversible omdannelse fra tilstanden \(P_2\), \(T_1\) til tilstanden \(P_2\), \(T_2\). For denne omdannelse er \(dP\) nul, og
Derpå,
Da \(\(\Delta S^{rev}=0\), er den reversible proces entydig; dvs. givet \(P_1\), \(T_1\) og \(P_2\), er systemets sluttemperatur bestemt. Vi finder \(T_2\) fra
\
For at forstå entropiændringen for den irreversible proces skal vi først bemærke, at der findes et uendeligt antal af sådanne processer. Der er intet unikt ved den endelige temperatur. Givet \(P_1\), \(T_1\) og \(P_2\) kan sluttemperaturen, \(T^*_2\), have en hvilken som helst værdi, der er i overensstemmelse med stoffets egenskaber. For at specificere en bestemt irreversibel proces skal vi specificere alle fire størrelser \(P_1\), \(T_1\), \(P_2\), \(P_2\) og \(T^*_2\). Når vi har gjort dette, kan vi imidlertid beregne entropiændringen for den irreversible proces,
\
ved at beregne entropiændringerne, når vi reversibelt fører systemet langs den isoterme totrinsvej fra \(P_1\), \(T_1\) til \(P_2\), \(T_1\) og derefter langs den isobare vej fra \(P_2\), \(T_1\) til \(P_2\), \(T^*_2\). Beregningen af \(\Delta S^{irrev}\) for denne reversible vej fra \(P_1\), \(T_1\) til \(P_2\), \(T^*_2\) anvender den samme logik som beregningen i det foregående afsnit af \(\Delta S\) for den reversible vej fra \(P_1\), \(T_1\) til \(P_2\), \(T_2\), \(T_2\). Forskellen er, at \(T^*_2\) erstatter \(T_2\) som den øvre grænse i temperaturintegralet. Trykintegralet er det samme. Vi har
\
Fra \(\(\Delta S^{irrev}>\Delta S^{rev}\) har vi
\
Da integranterne er de samme og positive, følger det, at \(T^*_2>T_2\), som hævdet ovenfor.
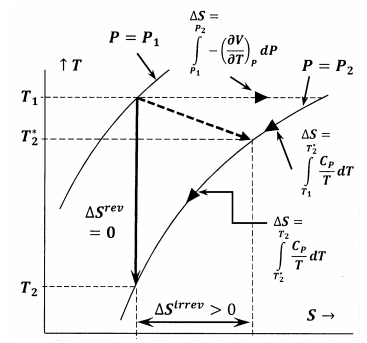
Figur 6 viser sammenhængen mellem de forskellige størrelser, der er diskuteret i dette argument. I første omgang viser figur 6 et plot af to af systemets isobarer i temperatur-entropirummet. Det vil sige, at linjen \(P=P_1\) viser det sæt af temperatur-entropipunkter, hvor det afbalancerede system har tryk \(P_1\); linjen \(P=P_2\) viser ligevægtspositionerne ved tryk \(P_2\). Andre linjer i denne skitse repræsenterer de baner, langs hvilke systemet kan undergå reversible ændringer ved konstant entropi eller konstant temperatur. Den stiplede linje repræsenterer den irreversible proces, hvor systemet går fra den tilstand, der er angivet ved \(P_1\), \(T_1\), \(T_1\) til den tilstand, der er angivet ved \(P_2\), \(T^*_2\). Denne linje er stiplet for at repræsentere det faktum, at systemets temperatur måske ikke er veldefineret under den irreversible proces.
Effektiv afkøling kan opnås ved hjælp af trykændringer, hvis systemet er en gas. For væsker og faste stoffer er \({{\left({\partiel V}/{\partiel T}\right)}_P\) imidlertid lille; følgelig er temperaturændringen for en reversibel trykændring også lille. Ved temperaturer nær det absolutte nulpunkt er næsten alle stoffer faste stoffer; for at opnå effektiv afkøling skal vi ændre en termodynamisk variabel, for hvilken et fast stofs temperaturkoefficient er så stor som muligt. For at overveje det generelle problem med at sænke temperaturen i et system ved at variere noget andet end tryk, må vi overveje et system, hvor en eller anden form for ikke-tryk-volumenarbejde er muligt. Et sådant system er udsat for en ekstra kraft, og dets energi ændres i takt med at denne kraft ændres.
Adiabatisk afmagnetisering
Den praktiske metode, hvormed man opnår ekstremt lave temperaturer, kaldes adiabatisk afmagnetisering. Denne metode udnytter egenskaberne ved paramagnetiske faste stoffer. I sådanne faste stoffer giver uparrede elektroner, der er lokaliseret på de enkelte atomer, anledning til et magnetisk moment. Kvantemekanikken fører til vigtige konklusioner om vekselvirkningen mellem sådanne magnetiske momenter og et påført magnetfelt: I et påført magnetfelt er det magnetiske moment for et enkelt atom kvantiseret. I det enkleste tilfælde kan det kun være rettet i to retninger; det skal være enten parallelt eller antiparallelt med det påførte magnetfelt. Når et atoms magnetiske moment er parallelt med det magnetiske felt, er systemets energi mindre, end når det er antiparallelt. Det påførte magnetfelt udøver en kraft på de magnetiske momenter, der er knyttet til de enkelte atomer. Systemets energi afhænger af størrelsen af det påførte magnetfelt.
Snarere end at fokusere på det særlige tilfælde af adiabatisk afmagnetisering, lad os overveje de energi- og entropiforandringer, der er forbundet med ændringer i et generaliseret potentiale, \({\mathit{\Phi}}_{\theta }\), og dets generaliserede forskydning, \(\theta\). (Ved adiabatisk afmagnetisering vil \(\theta\) være det påførte magnetfelt). Tre variabler er nødvendige for at beskrive reversible ændringer i dette system. Vi kan udtrykke energien og entropien som funktioner af temperatur, tryk og \(\theta\):
\(E=E\left(T,P,\theta \right)\) og \(S=S\left(T,P,\theta \right)\). Det samlede differential af entropien omfatter et udtryk, der angiver entropiens afhængighed af \(\theta\). Vi har
\
hvor vi skriver \(C\left(T,P,\theta \right)\) for at understrege, at vores nuværende formål nu kræver, at vi måler varmekapaciteten ved konstant tryk og konstant \(\theta\).
For konstant tryk, P, og konstant forskydning, \(\theta\), afhænger entropien af temperaturen som
\
Postulatet om, at entropien skal være endelig ved enhver temperatur, indebærer, at den tryk- og \(\theta\)-afhængige varmekapacitet bliver nul ved det absolutte nulpunkt. Det vil sige, at ved det absolutte nulpunkt forsvinder varmekapaciteten uanset værdierne af P og \(\theta\). Argumentet er nøjagtig det samme som tidligere. Tidligere skrev vi \(C_P\venstre(0\højre)=0\); for det nuværende generaliserede tilfælde skriver vi \(C\venstre(0,P,\theta \højre)=0\).
Sådan følger det af postulatet om, at entropien bliver konstant ved det absolutte nulpunkt for alle værdier af de andre termodynamiske variabler, at der for to vilkårlige tryk \(P_1\) og \(P_2\) og for to vilkårlige værdier af den generaliserede forskydning, \({\theta }_1\) og \({\theta }_2\),
\
og dermed, at
\ og \
Vi ønsker at betragte en proces, hvor et system går fra den laveste temperatur, der er til rådighed i omgivelserne, til en endnu lavere temperatur. For at minimere den endelige temperatur skal denne proces foregå adiabatisk for at minimere den endelige temperatur. Det skal også være en mulig proces, således at \(dS\ge 0\). Lad os nu for enkelhedens skyld antage, at vi udfører denne proces ved et konstant tryk, \(P\), og at systemet går fra den tilstand, der er angivet ved \(P\), \(T_1\), \({\theta }_1\), til den tilstand, der er angivet ved \(P\), \(T_2\), \({\theta }_2\), hvor \(T_1>T_2\). Entropierne for disse to tilstande er
\ og \
Den entropiske ændring for denne proces er
\ \
\
Lad os nu antage, at den endelige temperatur er nul; dvs. \(T_2=0\), således at
\ Heraf følger, at \
hvor uligheden til højre følger af, at \(C\venstre(T,P,{\theta }_1_1\højre)>0\). Heraf følger det, at
\
hvilket er i modstrid med Lewis og Randalls erklæring af den tredje lov. Antagelsen om, at systemet kan nå det absolutte nulpunkt, fører til en modsigelse af Lewis og Randalls erklæring af den tredje lov. Hvis Lewis og Randalls udsagn er sandt, er det absolutte nulpunkt derfor uopnåeligt.
Det omvendte gælder også; det vil sige, at vi ud fra udsagnet om, at det absolutte nulpunkt er uopnåeligt, kan vi vise, at Lewis og Randalls udsagn er sandt. For at gøre dette omarrangerer vi ovenstående ligning for \(\(\Delta S\),
\\
Hvis vi nu antager, at Lewis og Randall-sætningen er falsk, kan udtrykket til højre være mindre end eller lig med nul. Integralet til venstre kan så være nul, i hvilket tilfælde systemet kan nå det absolutte nulpunkt. Hvis Lewis- og Randall-udsagnet er falsk, er det sandt, at systemet kan nå det absolutte nulpunkt. Derfor: Hvis systemet ikke kan nå det absolutte nulpunkt, er Lewis og Randall-sætningen sand.
Figur 7 og 8 viser disse idéer ved hjælp af konturplots i temperatur-entropirummet. Hver figur viser to konturlinjer. Den ene af disse konturlinjer er et sæt af temperatur- og entropiværdier, langs hvilke trykket er konstant ved \(P\) og \(\theta\) er konstant ved \({\theta }_1\). Den anden konturlinje er et sæt af temperatur- og entropiværdier, hvor trykket er konstant ved \(P\), og \(\theta\) er konstant ved \({\theta }_2\). Hældningen af en konturlinje er
\
Da varmekapaciteten altid er positiv, er denne hældning altid positiv.
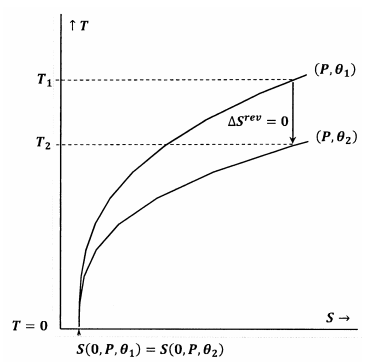
I figur 7 er Lewis- og Randall-udsagnet opfyldt. Når temperaturen går til nul, mødes konturlinjerne ved samme værdi af entropien; disse konturer opfylder forholdet
En adiabatisk (lodret) vej fra konturen for \(P\) og \({\theta }_1\) møder konturen for \(P\) og \({\theta }_2\) ved en positiv temperatur, \(T_2>0\). Da dette åbenbart er sandt for enhver \(P\) og enhver \({\theta }_2\), vil den endelige tilstand for enhver adiabatisk proces have \(T_2>0\). Da Lewis- og Randall-udsagnet er opfyldt, kan systemet ikke nå det absolutte nulpunkt, og omvendt.
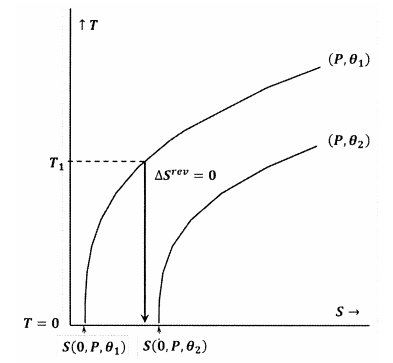
I figur 8 er Lewis- og Randall-udsagnet overtrådt, fordi vi har \(S\left(0,P,{\theta }_1\theta }_1\right)\). I dette tilfælde vil en adiabatisk proces, der indledes fra en tilstrækkelig lav begyndelsestemperatur, \(T_1\), nå det absolutte nulpunkt uden at skære konturen for konstant \(P\) og \({\theta }_2\). Da Lewis og Randals udsagn er overtrådt, kan systemet nå det absolutte nulpunkt, og omvendt.