1D & 3D-konvolutioner forklaret med… MS Excel!

Vi startede med 2D-konvolutioner i det første indlæg, fordi konvolutioner fik stor popularitet efter succeser inden for computervision. Da opgaver inden for dette domæne bruger billeder som input, og naturlige billeder normalt har mønstre langs to rumlige dimensioner (højde og bredde), er det mere almindeligt at se eksempler på 2D-konvolutioner end 1D- og 3D-konvolutioner.

Men på det seneste har der dog også været et stort antal succeser med at anvende konvolutioner på opgaver inden for naturlig sprogbehandling. Da opgaver inden for dette domæne anvender tekst som input, og tekst har mønstre langs en enkelt rumlig dimension (dvs. tid), passer 1D Convolutions godt ind! Vi kan bruge dem som mere effektive alternativer til traditionelle recurrent neural networks (RNN’er) såsom LSTM’er og GRU’er. I modsætning til RNN’er kan de køres parallelt for at opnå virkelig hurtige beregninger.

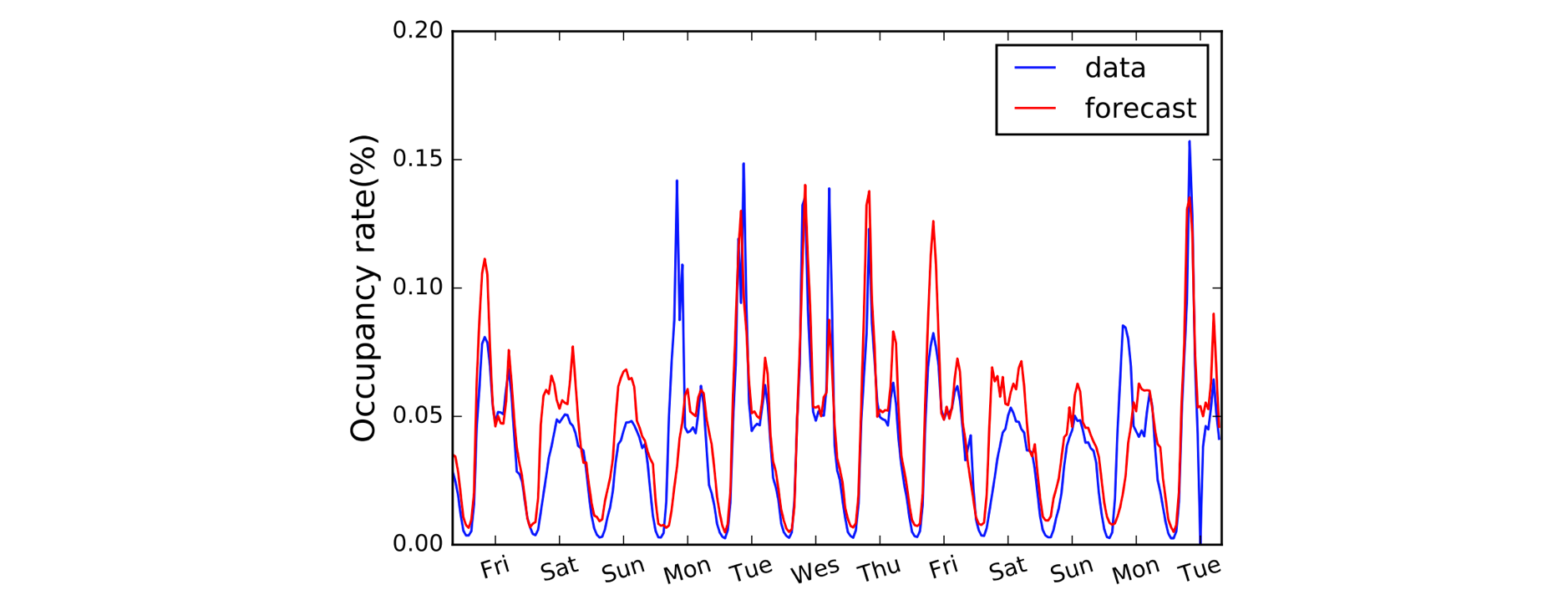
Et andet domæne, der har fordel af 1D Convolutions, er tidsseriemodellering. Som tidligere har vi en enkelt rumlig dimension på vores inputdata (dvs. tid), og vi ønsker at opfange mønstre over tidsperioder. Vi kalder ofte denne type data for “sekventielle”, fordi de kan ses som en sekvens af værdier. Og den rumlige dimension kalder vi ofte den “temporale” dimension. Det er også ret almindeligt at bruge 1D-konvolutioner før RNN’er: LSTNet-modellen er et eksempel herpå, og dens forudsigelser til trafikprognoser er vist nedenfor.

A, B, C. Det er nemt som (1,3,3) dot (2,0,1) = 5.

Med navngivningskonventionerne afklaret, lad os nu se nærmere på aritmetikken. Vi er heldige, for 1D-konvolutioner er faktisk bare en forenklet udgave af 2D-konvolutionen!

Ved beregning af en enkelt udgangsværdi kan vi anvende vores kerne af størrelse 3 på området af tilsvarende størrelse på venstre side af vores inputmatrix. Vi beregner “prikproduktet” af inputregionen og kernen, som for at opsummere er blot det elementvise produkt (dvs. multiplicer farveparrene) efterfulgt af en global sum for at opnå en enkelt værdi. Så i dette tilfælde:

(1*2) + (3*0) + (3*1) = 5

Vi anvender den samme operation (med den samme kerne) på de andre regioner i input arrayet for at opnå det komplette output array på (5,6,7,2); dvs. vi lader kernen glide over hele input arrayet. I modsætning til 2D-konvolutioner, hvor vi skubber kernen i to retninger, skubber vi for 1D-konvolutioner kun kernen i en enkelt retning; venstre/højre i dette diagram.

Videre: en 1D-konvolution er ikke det samme som en 1×1 2D-konvolution.

Kodning af tingene

Overraskende nok har vi brug for en Conv1D blok i Gluon til vores 1D-konvolution. Vi definerer kerneformen som 3, og da vi kun arbejder med en enkelt kerne i dette eksempel, angiver vi channels=1.

import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)

Vi kan nu sende vores input ind i conv-blokken ved hjælp af en foruddefineret kerne.

input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>

Hvad ændrer sig med padding, stride og dilation?

Vi så effekten af padding, stride og dilation i det sidste indlæg om 2D-konvolutioner, og det er meget ens for 1D-konvolutioner. Med padding padder vi kun langs en enkelt dimension (den tidsmæssige dimension) denne gang. Vores diagram repræsenterer tid på tværs af den vandrette akse, så vi polstrer til venstre og højre for inputdataene (og ikke over og under som i 2D-konvolutionseksemplet). Med stride og dilation anvender vi dem også kun langs den tidsmæssige dimension. Så et eksempel med padding og stride ville se således ud:

Vi tilføjer to yderligere argumenter i koden: padding=1 og strides=2.

conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>

Advanced: dimensionerne af inputdata skal overholde en bestemt rækkefølge, kaldet layout. Som standard forventer 1D-foldningen at blive anvendt på inputdata i formatet “NCW”, dvs. batchstørrelse (N) * kanaler (C) * bredde/tid (W). Og for 2D-konvolutioner er standardformatet “NCHW”, dvs. batchstørrelse (N) * kanaler (C) * højde (H) * bredde (W). Tjek layout-argumentet i Conv1D og Conv2D.