3D-rekonstruktion

I denne øvelse er det hensigten at programmere den nødvendige logik, så kobuki-robotten kan generere en 3D-rekonstruktion af den scene, som den modtager gennem sit venstre og højre kamera.

Installation

Installerer den generelle infrastruktur for JdeRobot Robotics Academy.

Hvordan kører du din løsning?

Navigér til mappen 3d_reconstruction

cd exercises/3d_reconstruction

Lancer Gazebo med verden kobuki_3d_reconstruction via kommandoen

roslaunch ./launch/3d_reconstruction_ros.launch

Derpå skal du udføre den akademiske applikation, som vil indarbejde din kode:

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

Hvordan skal du udføre øvelsen?

For at udføre øvelsen skal du redigere filen MyAlgorithm.py og indsætte din kode i den, som rekonstruerer 3d-punkter fra de to stereo-visninger.

Hvor skal du indsætte koden?

I filen MyAlgorithm.py,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Application Programming Interface

• self.getImage('left') – for at få det venstre billede
• self.getImage('right') – for at få det højre billede
• self.point.PlotPoint(position, color) – for at plotte punktet i 3d-værktøjet

Navigere i GUI-grænsefladen

Musbaseret: Hold og træk for at bevæge sig rundt i miljøet. Rul for at zoome ind eller ud

Tastaturbaseret: Piletaster til at bevæge sig rundt i omgivelserne. W- og S-tasterne til at zoome ind eller ud

Teori

I computervision og computergrafik er 3D-rekonstruktion processen med at bestemme et objekts 3D-profil samt at kende 3D-koordinaten for et hvilket som helst punkt på profilen. Rekonstruktion kan opnås på følgende måde:

• Hardware-baseret: Hardware-baseret tilgang kræver, at vi udnytter den hardware, der er specifik for rekonstruktionsopgaven. Anvendelse af struktureret lys, laserafstandsmåler, dybdemåler og radiometriske metoder er nogle eksempler.

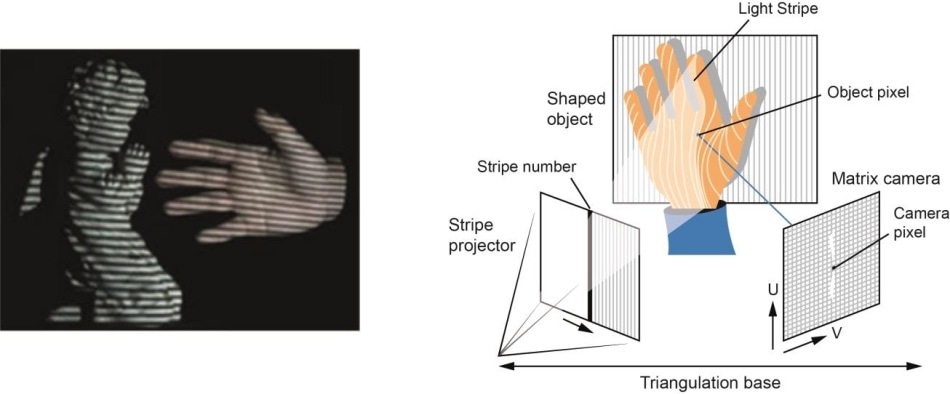
• Softwarebaseret: Software baseret tilgang er afhængig af computerens beregningsevner til at bestemme objektets 3D-egenskaber. Form ud fra skygge, tekstur, stereosyn og homografi er nogle gode metoder.

I denne øvelse er vores hovedformål at udføre 3d-rekonstruktion ved hjælp af softwarebaseret tilgang, især stereosyn 3d-rekonstruktion.

Epipolær geometri

Når to kameraer ser en 3D-scene fra to forskellige positioner, er der en række geometriske relationer mellem 3D-punkterne og deres projektioner på 2D-billederne, som fører til begrænsninger mellem billedpunkterne. Undersøgelsen af disse egenskaber og begrænsninger kaldes epipolær geometri. Nedenstående billede og forklaring kan generalisere ideen:

Sæt, at et punkt X i 3d-rummet afbildes i to visninger, på x i den første og x' i den anden. Ved at tilbageprojicere strålerne til deres kameracentre gennem billedplanerne får vi en plan overflade, betegnet π.

Såfremt vi nu antager, at vi kun kender x, kan vi spørge, hvordan det tilsvarende punkt x' er indskrænket. Planet π er bestemt af basislinjen(linje, der forbinder kameraets centre) og strålen defineret af x. Fra ovenstående ved vi, at den stråle, der svarer til det ukendte punkt x', ligger i π, og derfor ligger punktet x' på skæringspunktet l' mellem π og det andet billedplan. Denne linje kaldes den epipolære linje, der svarer til x. Denne relation hjælper os til at reducere søgeområdet for punktet i det højre billede fra et plan til en linje. Nogle vigtige definitioner, der skal bemærkes, er:

• Epipolen er skæringspunktet mellem den linje, der forbinder kameraets centre (basislinjen) med billedplanet.

• Et epipolært plan er et plan, der indeholder basislinjen.

• En epipolar linje er skæringspunktet mellem det epipolære plan og billedplanet.

Stereo rekonstruktion

Stereo rekonstruktion er et specialtilfælde af ovenstående 3d rekonstruktion, hvor de to billedplaner er parallelle med hinanden og lige langt fra det 3d punkt, vi ønsker at plotte.

I dette tilfælde er den epipolære linje for begge billedplaner ens, og er parallel med planernes bredde, hvilket forenkler vores begrænsning bedre.

3D-rekonstruktionsalgoritme

Rekonstruktionsalgoritmen består af 3 trin:

1. Detekter funktionspunkterne i et billedplan
2. Detekter det funktionspunkt, der svarer til det, der er fundet ovenfor
3. Trianguler punktet i 3d-rummet

Lad os se på dem en efter en

Feature Point Detection

Feature Point Detection er et stort område, hvor flere algoritmer allerede er undersøgt. Harris Corner Detection- og Shi-Tomasi-algoritmerne anvender egenværdier til at finde et godt featurepoint. Men problemet er, at vi har brug for mange punkter til 3D-rekonstruktion, og disse algoritmer vil ikke være i stand til at give os et så stort antal funktionspunkter.

Derfor bruger vi kantpunkter som vores funktionspunkter. Der kan være tvetydighed i deres detektion i den næste fase af algoritmen. Men vores problem er løst ved at tage kanter som featurepunkter. En rigtig god kantdetektor er Canny Edge Detection Algorithm. Algoritmen er ret enkel og pålidelig med hensyn til at generere kanterne.

Feature Point Extraction

Brug af den epipolære begrænsning forenkler virkelig tidskompleksiteten af vores algoritme. For generelle 3d-rekonstruktionsproblemer skal vi generere en epipolær linje for hvert punkt i den ene billedramme og derefter søge i dette prøveområde efter det tilsvarende punkt i den anden billedramme. Genereringen af den epipolære linje er også meget let i vores tilfælde, det er blot den parallelle linjes iterpolation fra venstre billede til højre billedplan.

Tjek af korrespondancen mellem billederne involverer mange algoritmer, som Sum of Squared Differences eller Energy Minimization. Uden at gå meget i dybden er det også tilstrækkeligt for vores use case at bruge et simpelt korrelationsfilter.

Triangulering

Triangulering er i enkle vendinger blot at beregne, hvor 3d-punktet kommer til at ligge ved hjælp af de to bestemte punkter i billedplanerne.

I virkeligheden kan billedpunkternes position ikke måles nøjagtigt. For almindelige kameraer kan der være geometriske eller fysiske forvrængninger. Derfor ligger der en masse matematik bag minimeringen af denne fejl og beregningen af den mest nøjagtige 3d-punktprojektion. Se dette link for at få en simpel model.

Hinvisninger

Enkle tips gives for at hjælpe dig med at løse 3d_reconstruction-opgaven. OpenCV-biblioteket bruges i vid udstrækning til denne øvelse.

Setup

Ved hjælp af øvelsens API kan vi nemt hente billederne. Når vi har hentet billederne, er det også en god idé at udføre bilateral filtrering af billederne, fordi der er nogle ekstra detaljer, som ikke skal medtages under 3d-rekonstruktionen. Se illustrationerne for at se virkningerne af at udføre den bilaterale filtrering.

Beregning af korrespondancer

OpenCV har allerede indbyggede korrelationsfiltre, som kan kaldes via matchTemplate(). Pas på ekstreme tilfælde som f.eks. kanter og hjørner.

En god observation er, at punkterne til venstre vil have korrespondance i den venstre del og punkterne til højre vil have korrespondance i den højre del. Ved hjælp af denne observation kan vi nemt fremskynde beregningen af korrespondance.

Plotting the Points

Enten manuel eller OpenCV-baseret funktion triangulatePoints fungerer godt til triangulering. Du skal blot være opmærksom på alle matrixformer og -størrelser, mens du udfører de algebraiske implementeringer.

Hold øje med forskellen mellem simple 3D-koordinater og homogene 4D-koordinater. Se denne video for at få flere detaljer. Ved blot at dividere den komplette 4d-vektor med dens 4. koordinat får vi 3d-koordinaterne.

På grund af forskellige implementeringer hos brugerne kan brugeren være nødt til at justere skalaen og forskydningen af de triangulerede punkter for at gøre dem synlige og repræsenterbare i GUI-grænsefladen. Nedskalering af 3D-koordinatvektoren med en værdi mellem 500 og 1000 fungerer godt. Også en forskydning på 0 til 8 fungerer godt.

Illustrationer