En abelsk gruppe er en gruppe, hvor elementerne er indbyrdes ombyttelige (dvs. 
for alle elementer 
og 
). Abeliske grupper svarer derfor til grupper med symmetriske multiplikationstabeller.
Alle cykliske grupper er abeliske, men en abelisk gruppe er ikke nødvendigvis cyklisk. Alle undergrupper af en abelsk gruppe er normale. I en abelsk gruppe er hvert element i en konjugationsklasse for sig selv, og karaktertabellen omfatter potenser af et enkelt element kendt som en gruppegenerator.
I Wolfram Language repræsenterer funktionen AbelianGroup det direkte produkt af de cykliske grupper af grader 
, 
, ….
Ingen generel formel er kendt for at give antallet af ikke-isomorfe finitte grupper af en given gruppeorden. Antallet af nonisomorfe abelske finitte grupper 
af en given gruppeorden 
er dog givet ved at skrive 
som
 |
(1)
|
hvor 
er forskellige primfaktorer, så
 |
(2)
|
hvor 
er partitionsfunktionen, som er implementeret i Wolfram Language som FiniteAbelianGroupCount. Værdierne af 
for 
, 2, … er 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 3, 2, … (OEIS A000688).
De mindste ordener, for hvilke der findes 
, 2, 3, … ikkeisomorfe abelske grupper, er 1, 4, 8, 36, 16, 72, 32, 32, 900, 216, 216, 144, 144, 64, 1800, 0, 288, 128, … (OEIS A046056), hvor 0 betegner et umuligt antal (dvs. ikke et produkt af delingstal) af ikkeisomorfe abelske grupper. De “manglende” værdier er 13, 17, 19, 23, 23, 26, 29, 29, 31, 34, 37, 38, 38, 39, 39, 41, 43, 46, … (OEIS A046064). De største antal abelske grupper som en funktion af ordenen er 1, 2, 3, 5, 7, 11, 15, 15, 22, 30, 42, 56, 77, 101, … (OEIS A046054), som forekommer for ordenerne 1, 4, 8, 16, 32, 64, 128, 128, 256, 512, 512, 1024, 2048, 4096, 8192, … (OEIS A046055).
Den Kronecker-dekompositionsteorem fastslår, at enhver endelig abelsk gruppe kan skrives som et direkte produkt af cykliske grupper af prim-potens gruppeorden. Hvis en endelig gruppes gruppeorden er et primtal 
, findes der en enkelt abelsk gruppe af orden 
(betegnet 
) og ingen ikke-abelske grupper. Hvis gruppens orden er et primtal i kvadrat 
, findes der to abeliske grupper (betegnet 
og 
. Hvis gruppens orden er et primtal i kubik 
, er der tre abelske grupper (betegnet 
, 
og 
), og i alt fem grupper. Hvis ordenen er et produkt af de to primtal 
og 
, findes der præcis én abelsk gruppe af gruppeorden 
(betegnet 
).
Et andet interessant resultat er, at hvis 
betegner antallet af ikkeisomorfe abelske grupper af gruppeorden 
, så er
 |
(3)
|
hvor 
er Riemanns zetafunktion.
Tallene for abelske grupper af orden 
er givet ved 1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 14, 15, 17, 17, 18, 19, 20, 25, … (OEIS A063966) for 
, 2, …. Srinivasan (1973) har også vist, at
 |
(4)
|
hvor
 |
 |
 |
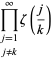(5)
|
 |
 |
 |
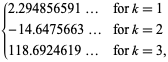(6)
|
(OEIS A021002, A084892 og A084893) og 
er igen Riemanns zetafunktion. Bemærk, at Richert (1952) fejlagtigt gav 
. Summene 
kan også skrives i de eksplicitte former
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
 |
 |
 |
(9)
|
DeKoninck og Ivic (1980) har vist, at
 |
(10)
|
hvor
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A084911) er et produkt over primtal 
, og 
er igen partitionsfunktionen.
Begrænsninger for antallet af ikkeisomorfe ikke-Abeliske grupper er givet af Neumann (1969) og Pyber (1993).
Der findes en række matematiske vittigheder, der involverer Abeliske grupper (Renteln og Dundes 2005):
Q: Hvad er lilla og kommuterer? Svar: En abelsk drue.
Q: Hvad er lavendel og pendler? Svar: En abelsk semigrape.
Q: Hvad er lilla, pendler og bliver tilbedt af et begrænset antal mennesker? Svar: En Abelsk drue, der kun er endeligt æret.
Q: Hvad er næringsrigt og pendler? Svar: En abelsk suppe.