Subtraktionsproceduren til eliminering af PL blev først udarbejdet for ca. to årtier siden. Denne procedure påvirker ikke de EKG-komponenter, der ligger i nærheden af PL-frekvensen. Denne teoretiske undersøgelse er udført for den grundlæggende PL-frekvens, men konklusionerne gælder også for dens harmoniske frekvenser og dermed for en vilkårlig interferensbølgeform. Procedurens effektivitet afhænger ikke af amplituden af interferensen, så længe forstærkeren ikke er mættet. Proceduren klarer desuden ændringer i amplitude og frekvens af interferensen. Proceduren er løbende blevet forbedret i årenes løb og implementeret i tusindvis af EKG-instrumenter og computerstøttede systemer . Lignende fremgangsmåder er også blevet offentliggjort af andre forskere.
- Principper
- Linært kriterium
- Kompensation af PL-amplitudevariationer
- Linear filtrering
- Kompensation af PL-frekvensvariationer
- Effektivitetsvurdering af proceduren
- Indflydelse af EMG-støj
- Interferensundertrykkelse i højopløsnings-EKG
- Sagen om batteriforsyede apparater og computerstøttede EKG-systemer
- Automatisk tilpasning til den nominelle PL-frekvens
- Udvikling af den teoretiske procedure
Principper
Subtraktionsproceduren anvendes oprindeligt med samplingfrekvensen f S , et multiplum af, og hardware synkroniseret med PL-frekvensen f PL . Proceduren består af følgende trin :
-
ECG-segmenter med frekvensbånd nær nul detekteres løbende ved hjælp af et passende kriterium. De betegnes som lineære segmenter og findes hovedsagelig i PQ- og TP-intervallerne, men også i tilstrækkeligt lange lige dele af R- og T-bølgerne.
-
Samplerne af disse segmenter er moving averaged, dvs. udsat for et lineært fasekamfilter med første nulpunkt sat ved f PL . De filtrerede prøver indeholder således ikke interferens.
-
Interferensamplituder, kaldet korrektioner, beregnes for hver af de faselukkede prøver, n, i PL-perioden, T PL , ved at subtrahere de filtrerede prøver fra de tilsvarende prøver i det forurenede (oprindelige) EKG-signal.
-
Det opnåede sæt korrektioner opdateres løbende i lineære segmenter og anvendes i ikke-lineære segmenter (normalt omkring QRS-komplekser og T-bølger med høj amplitude) til at subtrahere interferensen fra det oprindelige EKG-signal.
Et af de første resultater, der er opnået ved subtraktionsmetoden, er vist i fig. 1 . Interferens blev tilføjet til et rent simuleret EKG-signal for at evaluere fejlene og metodens effektivitet.
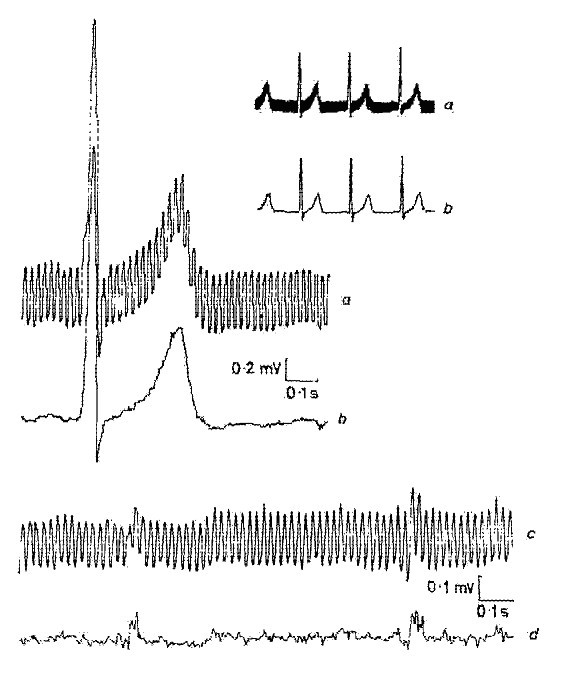
Et af de første resultater, der er opnået ved subtraktionsproceduren.
Linært kriterium
Et lineært kriterium, Cr, svarer normalt til den anden forskel i signalet (matematisk vurdering af lineariteten). Det første Cr er defineret på følgende måde. Seks på hinanden følgende første forskelle, FD i , beregnes ved hjælp af signalprøver, X i , med en afstand på én T PL :
FD i = X i+n – X i , for i = 1 … 6 (1)
Den PL-interferens i de første forskelle er undertrykt, hvis n = f S /f PL . I dette tilfælde er n = 5, da proceduren oprindeligt blev udviklet for nominelle f PL = 50 Hz og f S = 250 Hz. Endvidere tages den maksimale FD max- og den minimale FD min-værdi til bestemmelse af Cr:
Cr = | FD max – FD min | <M, (2)
hvor M er tærskelværdien.
Typiske lineære og ikke-lineære segmenter er vist i fig. 2. Det reelle EKG-signal (spor a) er overlejret af interferens (spor b). De lineære segmenter omfatter lavfrekvente signaler og strømliniefrekvenskomponenter. Et omtrentligt frekvensspektrum af sådanne lineære segmenter er vist i fig. 3.

Typiske lineære og ikke-lineære segmenter i det reelle EKG-signal.
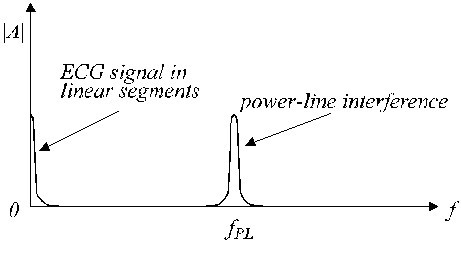
Opnærmet frekvensspektrum for et lineært segment.
Dette kriterium fungerer præcist, men kan næppe anvendes i realtid, fordi det er relativt langsomt at gennemføre. Denne ulempe overvindes af Christov og Dotsinsky, der anvender et modificeret kriterium med kun to efterfølgende forskelle.
Cr = | FDi+1- FD i | <M. (3)
Den første prøve, som ikke opfylder ligning (3), er forbundet med begyndelsen af et segment uden linjeføring. I overgangen fra ikke-lineær til lineær skal ligning (3) opfyldes n gange i træk for at undgå for tidlig registrering af det lineære segment. Kriteriet er implementeret i realtid for f S = 400 Hz og n = 8.
Senere definerede Dotsinsky og Daskalov kriteriet som to ikke-suekvenserende forskelle:
Cr = |FDi+k- FD i | <M, for k >1 (4)
Denne fremgangsmåde gør overgangen fra lineært til ikke-lineært segment mere præcis.
Kompensation af PL-amplitudevariationer
Desto hyppigere korrektionerne opdateres, desto bedre kompenseres amplitudevariationer i PL’en. Derfor skal tærsklen for det lineære kriterium, M, være rimeligt mindre restriktiv, således at de fejl, der begås ved at beregne gennemsnit af nogle segmenter, der afviger fra det ideelle lineære signal, er mindre end de fejl, der vil opstå, hvis M udløser sporadisk opdatering af korrektionen. I første omgang blev M fastsat til 160 μV . Senere blev heuristiske værdier fundet til M = 150 μV og M = 100 μV .
Linear filtrering
For ulige prøveantal n = 2m + 1 i en periode af PL-interferensen, er den filtrerede værdi:
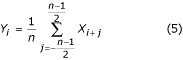
faseoverensstemmende med den ikke-filtrerede.
I tilfælde af et lige antal n = 2m er de to værdier faseforskudt med en halv prøveperiode:
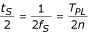
men bliver sammenfaldende i fase ved hjælp af formlen
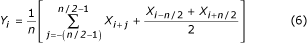
Det er muligt at foretage middelværdiberegning for hver anden, tredje eller qte prøve, hvis n/q er heltal. Afhængigt af om n/q er ulige eller lige, anvendes henholdsvis ligning (7) eller (8).

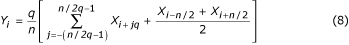
Et særligt tilfælde af maksimal stikprøvereduktion opstår med q = n/2 . Den tilsvarende formel:
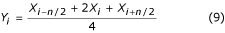
kaldes “trepunktsfilter”. Ud over ligning (8) kan følgende formel
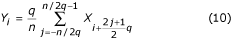
også anvendes, hvis q er lige. I tilfælde af q = n/2 bliver filteret “to-punkts” og er repræsenteret ved:

Et reduceret antal prøver i en periode med interferens vil føre til en øget stejl hældning af kamfilterets lobes og vil forkorte beregningstiden. Disse “fordele” skal dog vurderes omhyggeligt for ikke at overtræde Nyquist-reglen med en stor mængde af den tredje harmoniske frekvens. De øvrige overtoner tages ikke i betragtning, da de højeste ulige overtoner normalt undertrykkes af lavpasfiltre med cut-off i intervallet 100-150 Hz, mens de lige overtoner praktisk talt er fraværende på grund af den præcise polfremstilling af elværkernes generatorer.
Kompensation af PL-frekvensvariationer
Den tilladte afvigelse fra den nominelle PL-frekvens er i nogle lande begrænset til 1 % i henhold til standarderne. I praksis er afvigelsen ofte større. Kumaravel et al. rapporterede om en variation på 3%. McManus et al. fandt betydelige ændringer i interferensfrekvensen, som er overlejret på optagelser fra Common Standards for Electrocardiography (CSE) databasen.
Frekvensvariationer fører til et specialtilfælde af ikke-multipel prøvetagning med reelle n i stedet for heltal. Denne komplikation kan omgås, hvis afvigelserne opdages ved kontinuerlig hardwaremåling af f PL og korrigeres ved små justeringer af prøveintervallet t S omkring dets nominelle (R) værdi, t RS = T RPL /n (her er T RPL = 20 ms det nominelle T PL for f RPL = 50 Hz). For f PL , afvigelse mellem 49,5 og 50,1 Hz, er t S-variationerne i størrelsesordenen 1 %, og de indfører derfor ikke fejl, der ligger ud over den accepterede målenøjagtighed for parametre, der normalt anvendes til automatisk EKG-klassifikation.
En første fremgangsmåde forbinder udløsningen af hver første prøve, S 1 , af sekvenserne S k (k = 1, 2…n) i perioderne T PL med en vilkårligt valgt, men konstant amplitude af PL-spændingen. De næste prøver, S k (k = 2…n), er adskilt med t S , som fås ved t S = T RTL /n. For 50 Hz og n = 5 er t S = 4 ms. Dotsinsky og Daskalov har undersøgt to typer af fejl, der begås ved hjælp af denne fremgangsmåde. Den første, som skyldes uregelmæssigheder mellem prøverne, kan nå op på 1 % ved f S = 400 Hz og 1,2 % ved f S = 250 Hz i tilfælde af 1 % afvigelse omkring f RPL . Den anden type fejl overstiger ikke 3% og er en følge af den yderligere forskudte placering af den filtrerede prøve.
Dotsinsky og Daskalov rapporterede en forbedret metode. Den igangværende periode T PL måles og divideres med n. Den opnåede t S anvendes i den efterfølgende T PL .
Effektivitetsvurdering af proceduren
Eksempler på subtraktionsproceduren er vist i fig. 4 og fig. 5. EKG-signalerne er hentet fra American Heart Association-databasen. Signalerne er notch-filtreret for at undertrykke 60 Hz (PL-frekvens i USA) interferens. Derefter blandes signalerne med 50 Hz-interferens, amplitudemoduleret fra 0 til 3,2 mVp-p med en hastighed på 200 μVs-1. Sporene er identificeret som følger: i) indgangssignal; ii) syntetiseret interferens; iii) blandet signal; iv) behandlet signal; v) forskel mellem originalt og behandlet signal og vi) zoomet forskel. Faktisk omfatter de frasorterede komponenter også elektromyografisk (EMG) og andre støj. En ikke-undertrykt del af signalet samt små restinterferencer og forvrængninger som følge af kompromis med M-værdien er også til stede i forskellene.
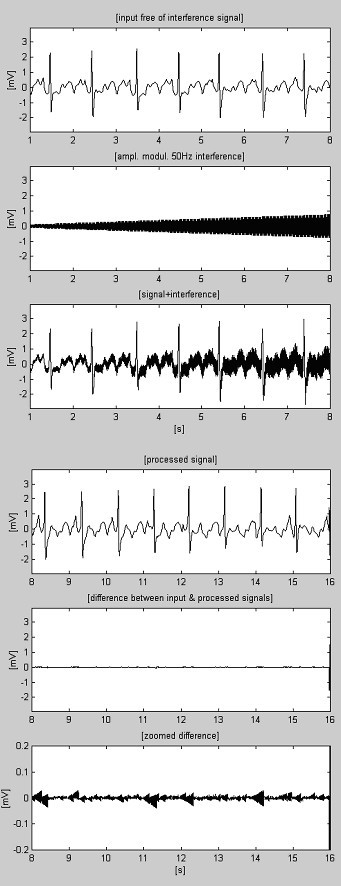
Behandlet AHA 3004d1-optagelse.
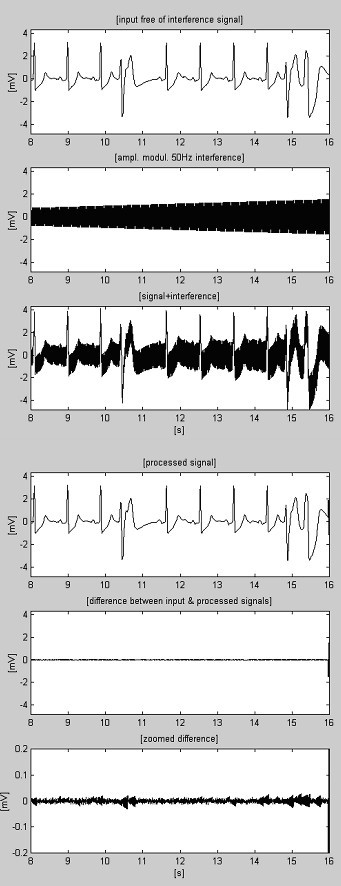
Behandlet AHA 6007d1-optagelse.
Der anvendes to signaler til at vurdere effektiviteten af subtraktionsproceduren med hensyn til kun interferensen. Det første, der er taget fra vores egen database, kaldes betinget “rent” (fig. 6). Resultatet viser små forskelle mellem input- og bearbejdede signaler, hvilket visuelt skyldes den støj, der er til stede i input-signalet. Dette resultat er verificeret med det andet syntetiserede signal, som ikke indeholder nogen forstyrrelser (fig. 7). Som det kan ses, indføres der ingen forvrængninger. Det samme syntetiserede signal overlejres af forstyrrelser og behandles (fig. 8). Der kan ikke findes nogen resterende forstyrrelser.
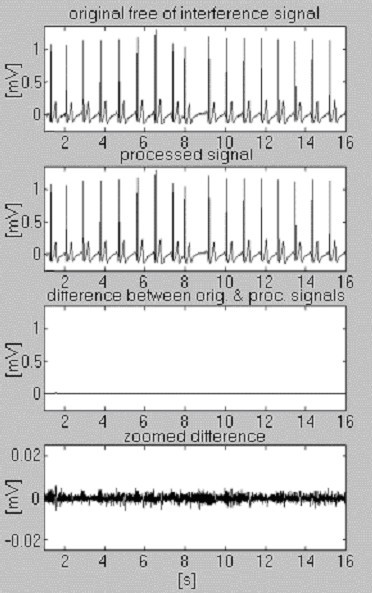
Bearbejdning af betinget “rent” signal.
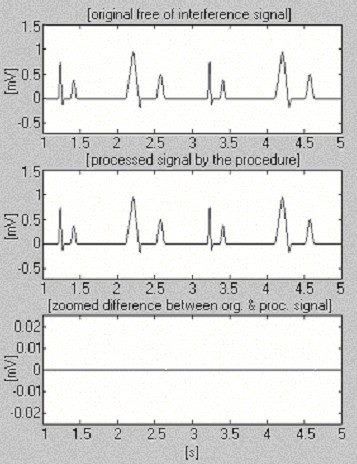
Bearbejdning af syntetiseret signal.
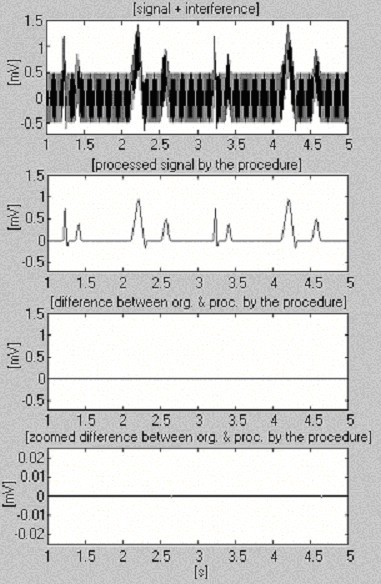
Bearbejdning af syntetiseret signal+interferens.
Indflydelse af EMG-støj
I nogle tilfælde er EMG-støjen så høj, at den lineære segmentbestemmelse vanskeliggøres. Som følge heraf vil upræcise korrektioner, som ikke svarer til den sidste ændring af interferensamplituden, medføre fejl (se reststøjen mellem 11. og 14. s i fig. 9).
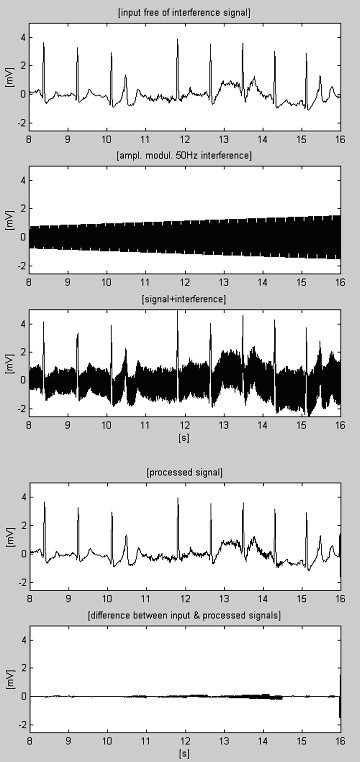
Behandlet EKG-signal+EMG-støj+interferens.
En meget enkel metode til undertrykkelse af EMG-støjens indflydelse på proceduren introducerer en ekstra parallel buffer, hvor igangværende dele af signalet ubetinget gennemsnitliggøres . Denne buffer anvendes til nøjagtig linearitetsdetektion. Fig. 10 og fig. 11 viser sammenligningen af resultaterne uden og med den parallelle buffer. Sporene “a” repræsenterer et EKG-signal blandet med interferens og EMG-støj. Sporene “b” i fig. 10 og “c” i fig. 11 viser overgange fra lineære til ikke-lineære segmenter (on-off-funktioner). Som det fremgår, er den midlede signaldel i fig. 10 meget begrænset. Som følge heraf er procedurens effektivitet reduceret (fig. 10c og 10d. I modsætning hertil gør den parallelle buffer det muligt at detektere lange lineære segmenter (fig. 11c), og reststøjen i det behandlede signal (fig. 11d) er lav. Støjen er dog ikke helt undertrykt, fordi en del af den deltager i korrektionsberegningen.
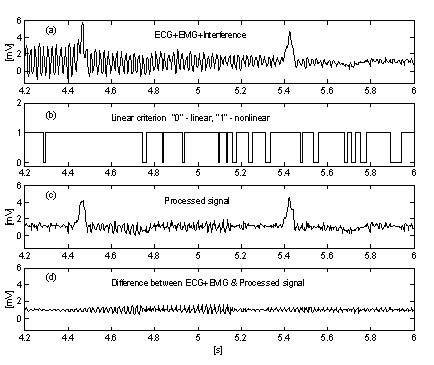
Subtraktion af interferens+EMG-støj uden parallelbuffer.
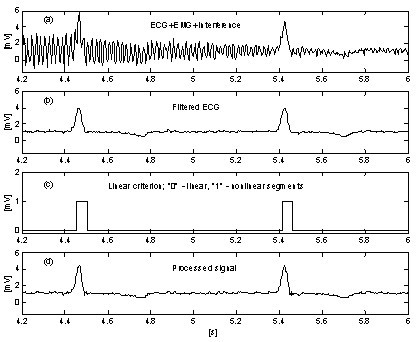
Subtraktion af interferens+EMG-støj med parallelbuffer.
En yderligere forbedring af EMG-støjundertrykkelsen opnås af Christov ved at anvende den adaptive tærskelværdi M, som beregnes i forhold til støj/signalforholdet Rt, defineret som Rt = S NL /S F , hvor støjniveauet S NL er lig med den summariske bredde af de ikke-lineære segmenter i en epok S F , der omtrent svarer til det pågældende RR-interval. Linearitetssøgning med et kriterium på M = 150 μV for “rent” EKG (fig. 12a) og for det samme signal, men forurenet med EMG-støj (fig. 12b), viser forskellige S NL , (fig. 12c og 12d). Metoden er udviklet i MATLAB-miljøet. Den indledende tærskel M er valgt lig med 30 μV. Derefter øges den gradvist, indtil Rt når op på 10 %, hvorefter subtraktionsproceduren påbegyndes. Niveauet Rt ≤ 0,1 foreslås af forholdet “QRS-bredde i forhold til RR-intervallet”, som normalt ligger på ca. 10 %. Elimineringen af både interferens og EMG-støj kan observeres i fig. 13b og 13d, hvor M = 420 μV anvendes. Til sammenligning behandles det “rene” EKG-signal med M = 35 μV (fig. 13a og 13c).

Støjniveauer SNL (spor c og d) i henholdsvis det “rene” EKG-signal (spor a) og det EMG-forurenede signal (spor b).
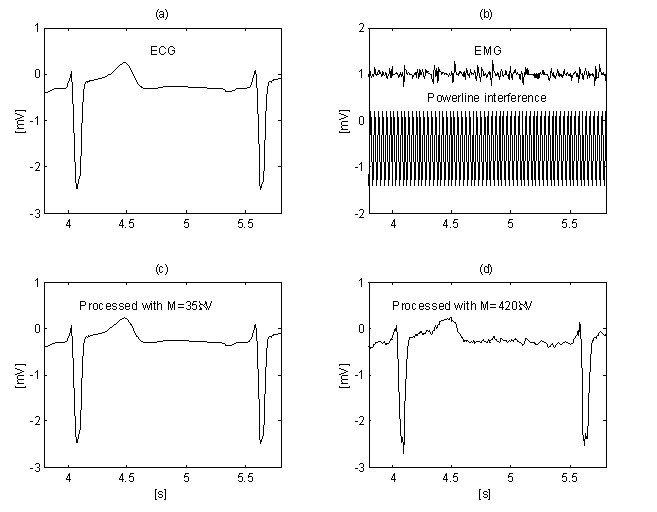
Undertrykkelse af interferens+EMG-støj ved hjælp af adaptiv tærskel M: “rent signal” (a) behandlet med M = 35 μV (c) og kontamineret signal (b) underkastet proceduren med M = 420 μV (d).
Lineære segmenter kan ikke regelmæssigt findes hos patienter med atrie- og ventrikelflimmer. Det er imidlertid ikke nødvendigt at bevare bølgeformen fuldstændigt for at kunne påvise fibrillering, og derfor kan alle former for traditionelle filtre anvendes.
Interferensundertrykkelse i højopløsnings-EKG
Subtraktionsproceduren kan ikke anvendes direkte på His-ekg med kropsoverflade, da His-bølgen med lav amplitude og relativt lav frekvens ikke kan skelnes i lineære segmenter. His-bølgen vil derfor i praksis blive undertrykt eller endog fjernet fra signalet. EMG-støjen har normalt en højere amplitude og et meget højere frekvensindhold sammenlignet med His-bølgen fra overfladen. Derfor resulterer en simpel ændring af tærskelværdien, M, ikke i en acceptabel afgrænsning af lineære og ikke-lineære segmenter.
Bazhina et al. gennemførte følgende ændring. Begyndelsen af det detekterede ikke-lineære segment før et QRS-kompleks forskydes 100 ms til venstre, hvorved His-bølgeområdet defineres som et ikke-lineært segment som standard (fig. 14).
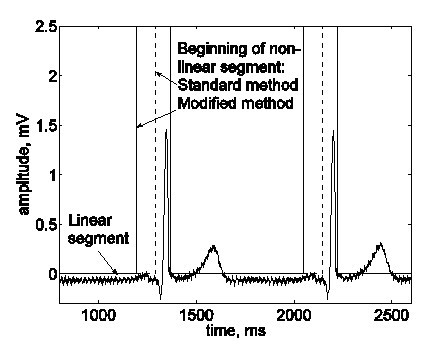
Begyndelsen af et ikke-lineært segment, herunder QRS-komplekset, blev som standard forskudt 100 ms til venstre, så det omfatter den zone, hvor His-bølgen forventes at optræde.
Subtraktionsproceduren og tre andre metoder: notch-filter, spektral interpolation , og regressionssubtraktion er testet mod minimal forvrængning af det oprindelige signal . Subtraktionsproceduren og regressionssubtraktionsproceduren viste sig at være de bedste, da Baratta et al. anvender et lignende koncept til støjestimering i lineære segmenter. Regressions-subtraktion håndterer dårligt amplitudeændringer af interferensen inden for det aktuelle segment.
Sagen om batteriforsyede apparater og computerstøttede EKG-systemer
Hardwaremåling af f PL , der er nødvendig for at kompensere for interferensfrekvensmodulationen, er ikke mulig i batteriforsyede apparater og i nogle computerstøttede EKG-systemer. Dotsinsky og Stoyanov har undersøgt intervallet for frekvensændringer af interferens med konstant amplitude, for hvilke den resterende del begrænses til acceptable niveauer uden brug af synkroniseret sampling. De fandt, at restinterferens under 20 μVp-p kunne opnås med proceduren ved: i) interferensamplitude ≤ 0,4 mVp-p og ii) frekvensændring med en hastighed ≤ 0,0125 Hzs-1. Da sådanne krav til strømforsyningen ofte kan overskrides, blev der udviklet en software til måling af interferens.
EKG-signalet behandles indledningsvis med et 49-51 Hz båndpasfilter. Amplituderne af to tilstødende prøver, Br L og Br R , der er taget fra en positiv hældning af interferensen, som er placeret under og over nullinjen, måles (fig. 15). Afstanden, t CP , mellem krydsningspunktet CP og den højre prøve, Br R , beregnes løbende ved:
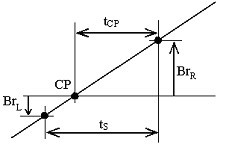
Interferensens nulpunktsoverskridelse.

I tilfælde af ændring af T PL redefineres t S ved hjælp af

Denne fremgangsmåde blev implementeret i MATLAB-miljøet. For samplingfrekvensen f S = 500 Hz og f RPL = 50 Hz er n lig med 10. Produktet kn bestemmer den tid, der anbefales at gå, før den nye tCP,i + kn beregnes og erstattes af den tidligere tCP,i. Fig. 16 viser et behandlet 1 mV EKG-signal efter at være blevet blandet af interferens med 2 mVp-p konstant amplitude og ekstremt hurtig variation med 1 Hz pr. 8 s frekvens (første spor). For at vurdere den opnåede effektivitet vises også den indzoomede forskel uden synkroniseret prøvetagning (sidste spor).
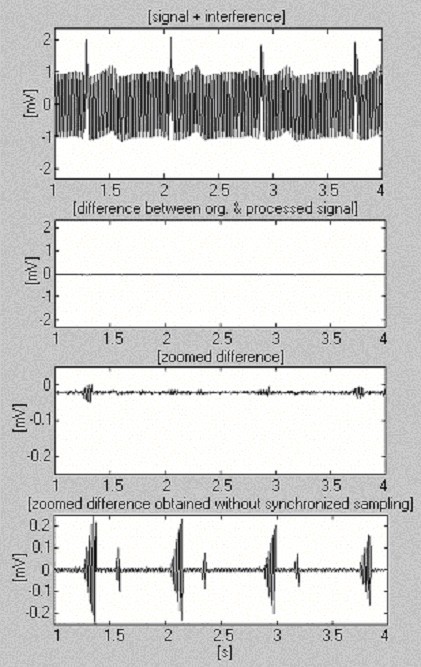
Subtraktionsprocedure ved hjælp af software power-line frekvensmåling.
Det næste logiske skridt, der skal tages, består i: i) at bibeholde EKG-instrumentets nominelle t S , ii) at re-sample signalet i overensstemmelse med den løbende målte f PL for at fjerne interferensen og iii) at vende tilbage til den nominelle t S . De første resultater af en sådan fremgangsmåde er meget lovende . Således vil softwarekompensationen af den variable f PL , såvel som en fuldstændig gennemførelse af subtraktionsproceduren i et instrument, herunder automatisk justering for f RPL på 50 eller 60 Hz, kunne gennemføres uanset hardwarekredsløb og den tilsvarende software.
Automatisk tilpasning til den nominelle PL-frekvens
Et fælles program til alternativ interferenssubtraktion i 50- og 60 Hz-miljø fører til ikke-multipel sampling, dvs. til reelt n. Almindeligt anvendte værdier af t S for f RPL = 50 Hz, f.eks. 250, 500 og 1000 Hz, svarer til irrationelle n på 4.1(6), 8.3(3) og 4.1(6), hvis 60 Hz-interferens skal elimineres. I det omvendte tilfælde, f S = 360 Hz, kræves n = 7,2. Afrundede værdier n* er uacceptable at anvende, da de vil medføre betydelige fejl.
Dotsinsky og Stoyanov har fundet en meget enkel løsning, der ikke kræver ændring af f S , og som ikke kræver ændring af f S . Den oprindelige procedure anvender et kamfilter over en periode, T PL , af interferensen. Programmet kører således hurtigere. Generelt kan n tages fra k > 1 hele perioder. Proceduren fungerer, hvis:
n = kT PL /t S er et helt tal.
For t S = 2 ms (f S = 500 Hz) og f RPL = 50 Hz er den mindste værdi af k, der opfylder ligning (14), reelt k = 1. I tilfælde af 60 Hz er k dog lig med 3. Der vil også forekomme nuller i forbindelse med underharmoniske 20 og 40 Hz, men de har ingen indflydelse på proceduren. Derfor er det helt tilstrækkeligt at skifte n mellem 10 (k = 1) og 25 (k = 3) for at operere med begge interferenser. Til dette formål kontrollerer to digitale båndpasfiltre det indgående signal. Figur 17 viser, at filteret med frekvensbånd, der overlapper interferensen, genererer et udgangssignal, der er en størrelsesorden højere end det andet filter.
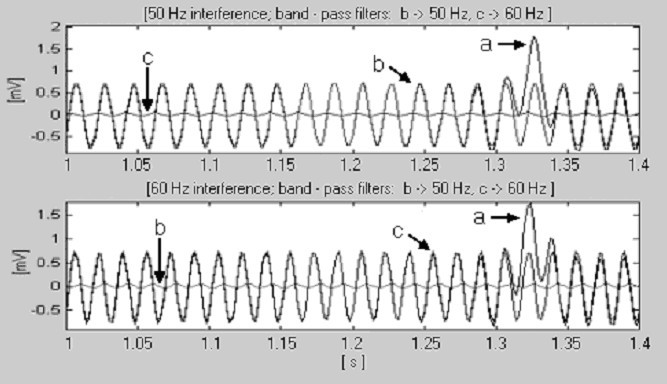
Detektion af den nominelle netfrekvens, a) en del af QRS-komplekset, b) 50 Hz-interferens og c) 60 Hz-interferens.
Udvikling af den teoretiske procedure
Theorien om subtraktionsproceduren blev videreudviklet af Mihov , Levkov og Mihov , og Mihov et al. De foreslog fire typer filtre, der er implementeret i en generaliseret struktur, som kan overvinde problemerne med næsten alle tilfælde af ikke-multipel prøvetagning, herunder variationer i interferensfrekvenser, uden brug af synkroniseret AD-konvertering.
Det såkaldte D-filter ved multipel sampling er defineret som er Cr i ligning (2), hvor den anden forskel, D i , opnås med FD s , der er adskilt med en T PL :
D i = (X i+n – X i ) – (X i – X i-n ) = X i-n – 2X i + X i+n (15)
D-filterets overføringsfunktion har nuller ved f = 0 og f = f PL Hz, som er vist lig med 50 Hz i fig. 18.

D-filterets overførselsfunktion for fPL = 50 Hz.
K-filteret beskriver det glidende gennemsnit, der præsenteres ved ligningerne (5) og (6). Dets overførselsfunktion er vist i figur 19 for n = 5 i tilfælde af ulige multiplicitet.
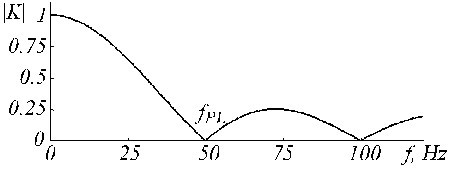
Overførselsfunktion for K-filter for fPL = 50 Hz og n = 5.
Den ligning, der anvendes til løbende beregning af interferenskomponenterne:
B i = X i – Y i (16)
definerer i virkeligheden et digitalt filter kaldet (1-K)-filter.
Dertil kommer, at filtrene omdefineres for ikke-multipel sampling, og f S = 250 Hz sammen med f RPL = 60 Hz tages i betragtning for at illustrere softwareforbedringen.
For at bevare overførselsfunktionens nuller skal D-filteret subtraheres med et korrektionsfilter med nul ved f = 0 og en forstærkning af D RPL ved f = f RPL , der er lig med forstærkningen af D-filteret for samme frekvens, f RPL . Syntesen af korrektionsfilteret er baseret på et trepunkts hjælpefilter givet ved ligningen:

hvor (n/2)* er den afrundede værdi af n/2.
Da A RPL er hjælpefilterets forstærkning for f = f RPL , multipliceres korrektionsfilteret med forholdet D RPL /A RPL . Ved hjælp af de tilsvarende overførselsfunktioner beregnes D RPL og A RPL på forhånd ved:
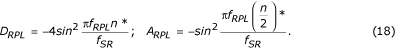
Sluttelig præsenteres det korrigerede D*-filter som

og er vist i fig. 20 ved spor “c”, hvor spor “a” og “b” er henholdsvis D-filteret og korrektionsfilteret.
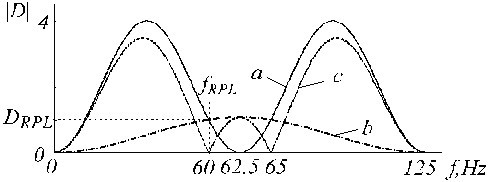
Transferfunktioner for a) D-filter, b) hjælpekorrektionsfilter og c) korrigeret D-filter.
K-filterets overføringsfunktion skal bevare nul for f = f RPL , unity gain for f = 0 og lineær fasereaktion. Proceduren for korrektion af K-filteret svarer til den foregående. Et hjælpefilter er givet ved den formel, der anvendes til beregning af korrektioner:
A i = X i – Y i , (20)
Filterets forstærkning er lig med 1 – K RPL for f = f RPL , hvor K RPL er K-filterets forstærkning for den samme frekvens f RPL . Hjælpefilteret multipliceres med K RPL /(1 – K RPL ) og trækkes fra K-filteret. Ligningen for det korrigerede K*-filter er:
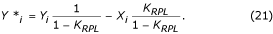
Konstanten K RPL kan estimeres ved:

for henholdsvis ulige eller lige multiplicitet.
Et eksempel på K-filterkorrektion er vist i fig. 21, hvor sporene “a”, “b” og “c” repræsenterer det primære K-filter, hjælpefilteret og det korrigerede K*-filter.
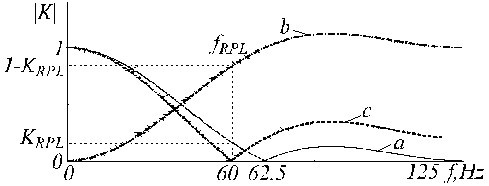
Transferfunktion af a) K-filter, b) hjælpekorrektionsfilter og c) korrigeret K-filter.
I tilfælde af ikke-multipel prøvetagning opstår der en faseforskel mellem de igangværende EKG-prøver og de interferenskomponenter B i (ligning 16), der normalt befinder sig i en midlertidig FIFO-buffer (first-in-first-out). Derfor skal B i ændres ved at blive subtraheret fra EKG-prøverne under ikke-lineære segmenter. Kompensationsproceduren er relativt kompliceret. Fig. 22 viser indholdet af den midlertidige buffer. Den aktuelle interferensprøve, B i-n *, er ikke sammenfaldende med den gendannede prøve, B i . Dens amplitude skal genberegnes for at kompensere for faseforskellen mellem dem. Dette gøres ved hjælp af et nyt filter med lineær fasegengivelse og forstærkning på én enhed for f = f RPL , kaldet B-filteret. Det syntetiseres ud fra det kendte K-filter med et vindue, der er lig med interferensperioden. I tilfælde af ulige n* kan det beskrives som:
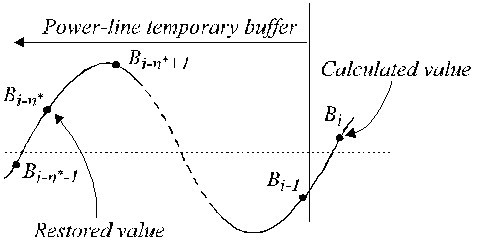
Restored værdier i den midlertidige buffer.
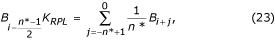
hvor K RPL er forstærkningen for interferensen i middelingsfilteret givet ved ligning (22).
Den genoprettede bufferværdi B i kan beregnes ved:
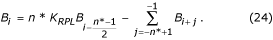
I tilfælde af lige n*:
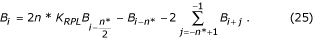
B-filterets overføringsfunktion er vist i fig. 23.
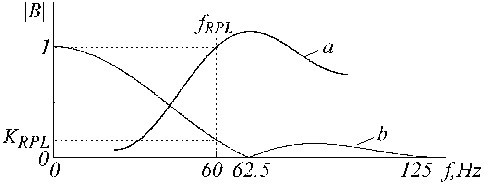
Transferfunktioner for a) B-filter og b) det kendte K-filter.
Den generaliserede struktur er vist i Fig. 24, hvor modulerne i subtraktionsproceduren er som følger:
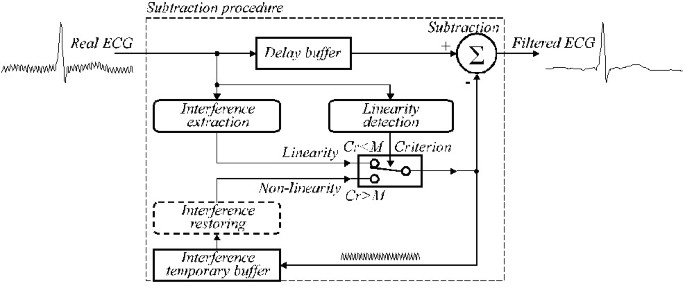
Generaliseret struktur for subtraktionsproceduren.
-
Linearitetsdetektion. D-filter anvendes til at evaluere lineariteten af hvert signalprøvekvarter.
-
Interferensudtrækning. (1-K)-filter anvendes til beregning af interferenskomponenten.
-
Kriterium. Betingelsen Cr <M sender enten ekstraheret eller genoprettet PL-interferens til subtraktion.
-
Interferens midlertidig buffer. Den ekstraherede eller gendannede interferenskomponent, der anvendes som korrektion i det ikke-lineære segment, gemmes på den position, der er låst med den igangværende fase af interferensen fra højspændingsledningen.
-
Interferensgendannelse. B-filter kaldes i tilfælde af ikke-multipel prøvetagning for at genoprette de sande korrektionsværdier, som skal subtraheres fra indgangssignalprøverne i ikke-lineære segmenter.
-
Delaybuffer. Kompenserer for den forsinkelse, der opstår ved D-filter og (1-K)-filter, og som er nødvendig, hvis proceduren køres i kvasirealtid. I modsat fald kan man se bort fra bufferen.
-
Subtraktion. Den ekstraherede eller gendannede interferensværdi subtraheres fra det forsinkede indgangssignal for at output “rent” EKG-signal. I tilfælde af ikke-linearitet implementerer både interferensudtrækning og subtraktion K-filteret.
En forbedret algoritme i overensstemmelse med den generaliserede struktur er blevet testet off-line. Resultaterne for f S = 250 Hz og f RPL = 60 Hz er vist i figur 25.
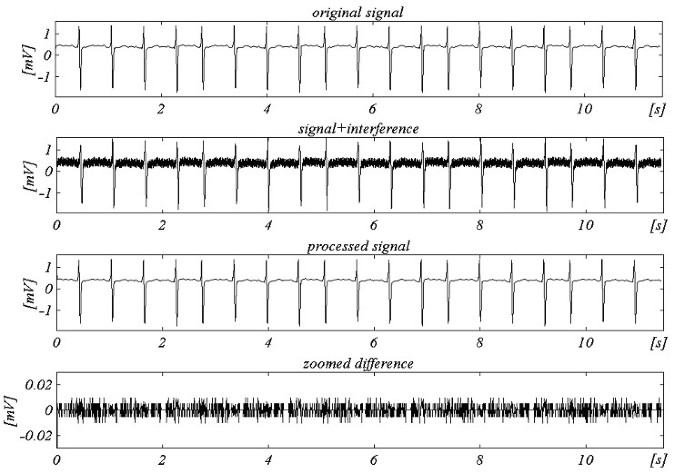
Eksempel for ikke-multipel sampling med fRPL = 60 Hz og fS = 250 Hz.