Abstract
Lyset bevæger sig gennem et vakuum med hastigheden c uanset lyskildens bevægelse og uanset observatørens referenceramme. Derfor tager det en vis tid for lyset at bevæge sig fra en lyskilde til en observatør i rummet, således at udsendelse af lys og iagttagelse af det udsendte lys ikke er samtidige. På baggrund af disse betragtninger foreslås en metode til måling af en observatørs absolutte hastighed, som kan anvendes til at bestemme et rumfartøjs bevægelsestilstand inde fra en lukket kabine. I denne undersøgelse introduceres også en ny forklaring på Lorentz-transformationen.
Nøgleord
koordinatsystem, referencesystem, bevægelse, absolut hastighed, relativitetsteori, lorentz-transformation, tid, rum, observatør, lyskilde
I den følgende analyse præsenteres en praktisk metode til måling af en observatørs absolutte hastighed, som kan bruges til at bestemme et rumfartøjs bevægelsestilstand inde fra en lukket kabine. Begrebet absolut hastighed henviser generelt til en ensartet standardhastighed for de forskellige objekter i et fysisk system i forhold til et postuleret ubevægeligt rum, der eksisterer uafhængigt af de fysiske objekter, der er indeholdt deri (dvs. et absolut rum). Heri præsenterer vi en tilgang baseret på rigid kinematik for at vise, at en observatørs absolutte hastighed kan bestemmes ud fra det faktum, at lys bevæger sig gennem et vakuum med hastigheden c uanset lyskildens bevægelse eller observatørens referenceramme. Der kræves derfor en vis tid til, at lyset bevæger sig fra en lyskilde til en observatør i rummet, således at udsendelsen af lys og observationen af det udsendte lys ikke er samtidige.
I den foreslåede analyse giver vi først følgende konventioner for de pågældende koordinatsystemer. Vi antager et kartesiansk koordinatsystem bestående af tre parvis vinkelrette akser med udgangspunkt i punktet (0,0,0,0), hvor ethvert punkt P i rummet kan defineres ved dets koordinater langs x-, y- og z-aksen, repræsenteret ved et ordnet par af reelle tal (x,y,z). Et inertialreferencesystem S antages at være repræsenteret ved et rektangulært rumkoordinatsystem (x,y,z), hvis oprindelse er O. En række standardure (benævnt S-ure) er placeret i stationære punkter i S. S-urene er gensidigt kalibreret (dvs. de giver ækvivalente aflæsninger på samme tidspunkt) på grundlag af udsendelse og modtagelse af et lyssignal. Nærmere bestemt projiceres der på tidspunktet tA en lysstråle fra ur A til ur B, som derefter på tidspunktet tB reflekteres af ur B tilbage mod ur A og ankommer til ur A på tidspunktet tA’. Hvis 
, er de to ure kalibreret. For enhver begivenhed, der befinder sig på koordinaterne x,y,z, er dens tidskoordinat t givet ved aflæsningen af det begivenhedsrelaterede S-ur. På samme måde etableres et andet inertialreferencesystem S’ baseret på et andet rektangulært rumkoordinatsystem (x’,y’,z’), hvis oprindelse er O’, og en anden række gensidigt kalibrerede standardure (S’-ure) er placeret på stationære punkter i referencesystemet S’. For enhver begivenhed, der befinder sig på koordinaterne x’,y’,z’, er dens tidskoordinat t’ givet ved aflæsningen af det begivenhedsrelaterede S’-ur.
Da rum- og tidskoordinaternes respektive oprindelser samt koordinataksernes retninger i vid udstrækning kan vælges vilkårligt, er de relationer mellem S og S’, der anvendes heri, baseret på følgende konventioner, som er anvendt for enkelhedens skyld.
(1) På et bestemt tidspunkt er de to systemers oprindelser og koordinatakser overlejret, og urene, der er placeret henholdsvis ved O og O’, er sat til nul, dvs, 
.
(2) x- og x’-akserne er sammenfaldende i retning af den relative bevægelse af S og S’; således er x og x’ til enhver tid sammenfaldende, mens y og y’ samt z og z’ er parallelle.
(3) S’ bevæger sig i S”s +x-retning.
Den foreslåede analyse er baseret på det grundlæggende princip om, at lys i et vakuum bevæger sig med en konstant hastighed c uanset bevægelsen af enten observatøren eller lyskilden. Således definerer vi heri observatørens absolutte hastighed U, som antages at være lineær og ensartet, som 
, hvor f(φ) repræsenterer en funktion af det geometriske forhold mellem retningen af et lyssignal og retningen af U, heri betegnet φ.
Den foreslåede analyse indeholder to nye forklaringer på relativiteten af tid og længde, som adskiller sig fra Einsteins forklaringer (se venligst “Om bevægelige legemers elektrodynamik”). Disse forklaringer introduceres i de følgende afsnit.
Tidsrelativiteten
I kraft af lysets begrænsede hastighed kræves der en vis tid for, at lyset kan bevæge sig fra en lyskilde til en observatør i rummet. Det kan derfor udledes, at udsendelse af lys og iagttagelse af lys ikke kan være samtidige. På grundlag af lysets konstante hastighed og de betingelser, der er illustreret i figur 1, definerer vi følgende faktorer. Positionerne af en lyskilde og en observatør på 
, hvor lyskilden udsender lys (betegnet som begivenhed R), er givet som henholdsvis A og H0. I løbet af lysets udbredelsesperiode fra 
til 
tilbagelægger observatøren en afstand U∙T fra position H0 til H, hvorefter observatøren modtager det udsendte lys. Følgelig definerer vi 
som afstanden l mellem observatørens position ved modtagelsen af lyssignalet ved 
og lyskildens position, når den udsender lys ved 
. På grund af lysets konstante hastighed er 
. Afstanden 
svarer til U∙T. Endelig definerer vi 
som afstanden l0 mellem observatørens position ved 
og lyskildens position ved 
. Her introducerer vi en betragtning af observatørens position ved 
, som tidligere blev anset for ikke at have nogen fysisk betydning. Hvis bevægelsestilstandene for observatøren og lyskilden er ækvivalente, er l0 givet, således at U kan beregnes via de trekantede relationer, der er illustreret i ,Figur 1.
I nærværende arbejde måles tiden for en begivenhed ved hjælp af følgende metode. Både observatøren og et ur er placeret ved oprindelsen. Når lyssignalet, der repræsenterer en hændelse, når frem til observatøren, vil lysets ankomsttidspunkt svare til det tidspunkt, som uret angiver. Fordelen ved denne korrespondance er, at den altid er relateret til positionen af den observatør, der anvender uret. Som det fremgår af figur 1, kan det rumlige punkt O3 defineres på grundlag af lyskildens position, når den udsender lys ved 
, og det rumlige punkt O2 kan defineres på grundlag af observatørens position, når den modtager lys ved 
. Det er imidlertid ikke indlysende, hvordan det rumlige punkt O1, hvor observatøren befinder sig, når lyskilden udsender lys ved 
, kan defineres. For at løse dette problem indføres begreberne absolut hvile (dvs. 
) og absolut bevægelse (dvs. 
). Vi erstatter henholdsvis den enkelte bevægelige observatør i H0 og H med to observatører H1 og H2 i hvile i henholdsvis rumlige punkter O1 og O2, mens lyskilden A er i hvile i rumligt punkt O3. Hver af observatørerne og lyskilden anvender kalibrerede standardure, og A udsender et lyssignal ved 
, der betegnes som begivenhed R0. Når observatør H1 modtager lyssignalet, der bevæger sig med c, er urets aflæsning T0, og når H2 modtager det, er aflæsningen T. Som sådan kan afstandene 
og 
defineres på grundlag af lyssignalets respektive rejsetider på følgende måde: 
, (1)
og
. (2)
I henhold til de trekantede relationer, der er vist i figur 1, er transformationen af begivenheden R0 mellem observatørerne H1 og H2 givet på følgende måde: 
(3) 
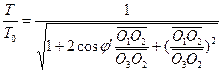(4)
Her er 
vinklen mellem linjen O3O1 og x-aksen, og 
er vinklen mellem linjen O3O2 og x-aksen.
Vi vender nu tilbage til den betingelse, at der er tale om en enkelt bevægelig observatør, og vi antager, at i system S anvender både observatør H og lyskilde A et kalibreret standardur. På tidspunktet for hændelsen R befinder lyskilde A sig i det rumlige punkt O3, og observatør H befinder sig i punkt O1. Det øjeblik, hvor lyssignalet når frem til det rumlige punkt O1, svarer til en aflæsning af S-uret på T0. Når observatør H modtager lyssignalet, er aflæsningen T, og H befinder sig i O2.
H kan naturligvis ikke observere hændelsen R i punkt O1. For at løse dette problem placeres en anden observatør H- i system S ved punkt O1 svarende til 
, hvor H-‘s position anvendes til at definere det rumlige punkt O1. Derefter kan transformationen af begivenhed R mellem observatørerne H- og H fås ved hjælp af ligning (3) som følger. 
(5)
Dermed kan ligningerne (3) og (4) omskrives på følgende måde: 
(6) 
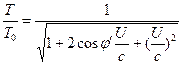(7)
e også bemærke, at for 
forenkles ligningerne (6) og (7) til følgende.
(8) 
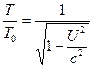(9)
Dermed kan der på baggrund af ovenstående analyse fås en simpel metode til bestemmelse af U ud fra ligning (6), forudsat at 
(φ) er kendt.
For enkelhedens skyld vælges som referenceramme en lyskilde med en bevægelsestilstand, der svarer til observatørernes bevægelsestilstand. En observatør er placeret i midten af en lige stiv stang i ensartet lineær bevægelse, og lyssignaler fra forskellige positioner på stangen ankommer til observatøren på forskellige tidspunkter. Observatøren registrerer stangens afbøjning ved observatørens position med en afbøjningsvinkel 
, som kan fås ud fra ligning (8).
Gennem denne metode kan bevægelsestilstanden for et rumfartøj bestemmes fra en lukket kabine.
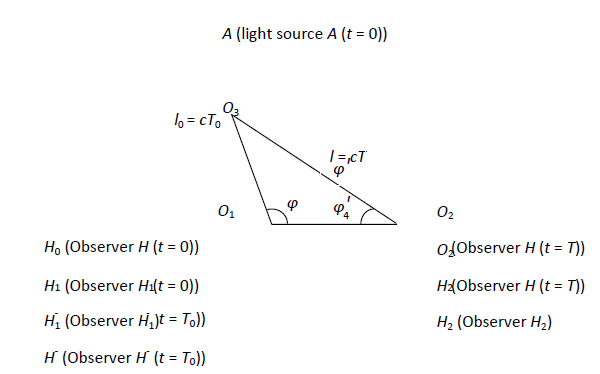
Figur 1: Bevægelsestilstande for observatøren og lyskilden
Længderelativiteten
I ovenstående analyse er der indført to længder, nemlig 
og 
. I dette tilfælde betragter vi længden af en stang, der antages at være en stationær stiv stang af længde L i sit koordinatsystem, for hvilken L måles med en stationær stavmåler, og hvor stangens akse er sammenfaldende med x-aksen i et koordinatsystem, der bevæger sig med en ensartet lineær bevægelse i +x-retningen med en absolut hastighed U. Det antages, at L bestemmes ved de to operationer, der er defineret nedenfor.
(a) Observatøren befinder sig i det samme bevægelige koordinatsystem som staven og stavmåleren, og L måles ved at lægge staven og stavmåleren over hinanden.
(b) Ved hjælp af flere ure, der er placeret i stationære koordinater, og som bevæger sig synkront, måler observatøren positionerne af stavens to ender i stationære koordinater på et bestemt tidspunkt t, og afstanden mellem de to positioner måles med den stationære stavmåler. 
er den længde, der er beregnet ved operation (a), og som her betegnes som stangens længde i det bevægelige koordinat. 
er den længde, der er beregnet ved operation (b), og som her betegnes som længden af en bevægelig stang i den stationære koordinat. Det er indlysende, at 
og 
er forskellige.
Vi antager, at i system S befinder observatør H- sig i samme bevægelsestilstand som H. Som det fremgår af figur 1, befinder H- sig i punkt O1, når han modtager lyssignalet ved 
, og samtidig befinder observatør H sig i punkt O4. Derfor er t=0,04
afstanden mellem H- og H ved 
, og 
. (10)
er den afstand, som observatør H tilbagelægger i intervallet fra T0 til T, således at
. (11)
er afstanden mellem H- ved 
og H ved 
, således at
. (12)
Sådan kan følgende udtryk udledes: 
(13)
Næst vil vi betragte koordinat- og tidstransformationerne mellem to bevægelige koordinatsystemer, som begge bevæger sig med en ensartet lineær hastighed, hvilket repræsenterer en ny forklaring på Lorentz-transformationen.
Hvis vi antager, at observatør H (i system S), observatør H’ (i system S’) og lyskilde A” (i system S”) alle anvender individuelt kalibrerede standardure, og at lyskilde A” ved 
udsender et lyssignal, betegnet som begivenhed R”. På tidspunktet for hændelsen R”’ befinder A” sig i punkt O3, og observatørerne H og H’ er sammenfaldende. Når observatør H modtager lyssignalet, er aflæsningen af S-uret T, og H befinder sig i punkt O1. Når observatør H’ modtager lyssignalet, er aflæsningen af S’-uret T’, og H’ befinder sig i punkt O2. Derefter kan transformationen af begivenheden R”’ mellem observatørerne H’ og H beregnes ud fra ligning (3), hvor
. (14)
Her er u den relative hastighed mellem observatørerne H’ og H, hvilket giver følgende transformationer. 
(15) 
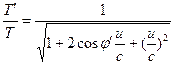(16)
Fra 
kan man udlede følgende relationer: 
. (17)
Ved 
og 
forenkles ligning (16) til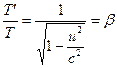
. (18)
Deraf kan følgende transformationsrelationer udledes:
, (19)
, (20)
, (21)
. (22)
Dertil kommer, at når 
, 
, (23)
og 
, (24)
, (25)
, (26)
. (27)