Toleranceintervaller
Dette afsnit indeholder statistiske oplysninger om ensidige og dobbeltsidede toleranceintervaller.
Intervaller baseret på normalfordeling
Ensidigt interval
Det ensidige interval beregnes på følgende måde:
Undergrænse = 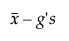
Overgrænse = 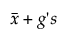
hvor
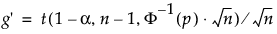
s er standardafvigelsen
t er kvantilen fra det ikke-central t-fordeling
Φ-1 er standardnormalkvantilen
To-sidet interval
Det tosidede interval beregnes på følgende måde:
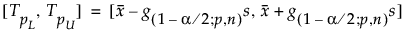
hvor s er standardafvigelsen, og g(1-α/2; p,n) er en konstant.
For at bestemme g skal man betragte den del af populationen, der er omfattet af toleranceintervallet. Tamhane og Dunlop (2000) angiver denne brøkdel som følger:
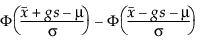
hvor Φ betegner den normale cdf (kumulative fordelingsfunktion) af standardnormal størrelse.
Dermed løser g følgende ligning:
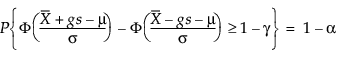
hvor 1 – γ er brøkdelen af alle fremtidige observationer, der er indeholdt i toleranceintervallet.
For yderligere oplysninger om toleranceintervaller baseret på normalfordeling henvises til tabellerne J.1a, J.1b, J.6a og J.6b i Meeker et al. (2017).
Nonparametriske intervaller
Ensidig nedre grænse
Den nedre 100(1 – α)% ensidige tolerancegrænse for at indeholde mindst en andel β af den udtagne fordeling fra en stikprøve af størrelse n er ordensstatistikken x(l). Indekset l beregnes som følger:
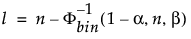
hvor Φ-1bin(1-α, n, β) er det (1 – α)-te quantile af binomialfordelingen med n forsøg og sandsynligheden for succes β.
Det faktiske konfidensniveau beregnes som Φbin(n-l, n, β), hvor Φbin(x, n, β) er sandsynligheden for, at en binomialt fordelt tilfældig variabel med n forsøg og sandsynlighed for succes β er mindre end eller lig med x.
Bemærk, at for at beregne et nedre ensidigt toleranceinterval uden fordeling skal stikprøvestørrelsen n være mindst lige så stor som 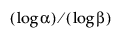 .
.
Ensidig øvre grænse
Den øvre 100(1 – α)% ensidige tolerancegrænse, der skal indeholde mindst en andel β af den udtagne fordeling fra en stikprøve af størrelse n, er ordensstatistikken x(u). Indekset u beregnes som følger:
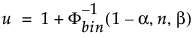
hvor Φ-1bin(1-α, n, β) er den (1 – α)-te kvantil af binomialfordelingen med n forsøg og sandsynlighed for succes β.
Det faktiske konfidensniveau beregnes som Φbin(u-1, n, β), hvor Φbin(x, n, β) er sandsynligheden for, at en binomialfordelt tilfældig variabel med n forsøg og sandsynlighed for succes β er mindre end eller lig med x.
Bemærk, at for at beregne et øvre ensidigt fordelingsfrit toleranceinterval, skal stikprøvestørrelsen n være mindst lige så stor som 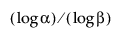 .
.
To-sidet interval
Det 100(1 – α)% to-sidede toleranceinterval, der skal indeholde mindst en andel β af den udtagne fordeling fra en stikprøve af størrelse n, beregnes som følger:
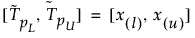
hvor x(i) er den i-te ordensstatistik, og l og u beregnes som følger:
Let ν = n – Φ-1bin(1-α, n, β), hvor Φ-1bin(1-α, n, β) er den (1 – α)-te kvantil af binomialfordelingen med n forsøg og sandsynlighed for succes β. Hvis ν er mindre end 2, kan der ikke beregnes et tosidet fordelingsfrit toleranceinterval. Hvis ν er større end eller lig med 2, er l = floor(ν/2) og u = floor(n + 1 – ν/2).
Det faktiske konfidensniveau beregnes som Φbin(u-l-1, n, β), hvor Φbin(x, n, β) er sandsynligheden for, at en binomialfordelt tilfældig variabel med n forsøg og sandsynlighed for succes β er mindre end eller lig med x.
Bemærk, at for at beregne et tosidet fordelingsfrit toleranceinterval skal stikprøvestørrelsen n være mindst lige så stor som n i følgende ligning:

For yderligere oplysninger om fordelingsfrie toleranceintervaller henvises til Meeker et al. (2017, sek. 5.3).