Das dritte Gesetz besagt, dass die Entropie eines Stoffes immer endlich ist und dass sie sich einer Konstanten nähert, wenn sich die Temperatur dem Nullpunkt nähert. Der Wert dieser Konstante ist unabhängig von den Werten aller anderen Zustandsfunktionen, die die Substanz charakterisieren. Für jede beliebige Substanz können wir dem Grenzwert für die Nulltemperatur einen beliebig gewählten Wert zuweisen. Wir können jedoch nicht allen Stoffen beliebige Null-Temperatur-Entropien zuordnen. Die von uns vorgenommenen Zuordnungen müssen mit den experimentell beobachteten Null-Temperatur-Grenzwerten der Entropieänderungen von Reaktionen zwischen verschiedenen Stoffen übereinstimmen. Für perfekt kristalline Stoffe sind diese Reaktionsentropien alle gleich Null. Wir können diese Bedingung erfüllen, indem wir der molaren Null-Temperatur-Entropie jedes Elements einen beliebigen Wert zuweisen und festlegen, dass die Null-Temperatur-Entropie einer beliebigen Verbindung die Summe der Null-Temperatur-Entropien der sie bildenden Elemente ist. Diese Berechnung wird stark vereinfacht, wenn man die Null-Temperatur-Entropie eines jeden Elements gleich Null setzt. Dies ist der wesentliche Inhalt des dritten Gesetzes.
Die Erklärung von Lewis und Randall enthält diese Auswahl des Null-Entropie-Bezugszustands für Entropien, indem sie ihn als „kristallinen Zustand“ jedes Elements bei null Grad spezifiziert. Infolgedessen ist die Entropie jeder Substanz bei null Grad größer oder gleich null. Das heißt, die Lewis-Randall-Erklärung enthält eine Konvention, die den Grenzwert der Entropie eines beliebigen Stoffes bei Null Grad festlegt. In dieser Hinsicht trifft die Lewis-Randall-Erklärung eine im Wesentlichen willkürliche Wahl, die keine intrinsische Eigenschaft der Natur ist. Wir sehen jedoch, dass es sich um eine äußerst bequeme Wahl handelt.
Wir haben alternative Aussagen zum ersten und zweiten Gesetz diskutiert. Eine Reihe von alternativen Aussagen zum dritten Gesetz sind ebenfalls möglich. Wir betrachten die folgenden:
Es ist unmöglich, eine Temperatur von absolut Null zu erreichen.
Diese Aussage ist allgemeiner als die Aussage von Lewis und Randall. Wenn wir die Anwendung dieser Aussage auf die Temperaturen betrachten, die bei Prozessen mit einer einzigen Substanz erreicht werden können, können wir zeigen, dass sie die Lewis- und Randall-Aussage impliziert und von ihr impliziert wird.
Die Eigenschaften der Wärmekapazität, \(C_P\), spielen bei diesen Argumenten eine zentrale Rolle. Wir haben gesehen, dass \(C_P\) eine Funktion der Temperatur ist. Obwohl dies nicht sinnvoll ist, können wir die definierende Beziehung für \(C_P\) auf eine Substanz anwenden, die einen Phasenübergang durchläuft, und finden \(C_P=\infty\). Wenn wir an einen Stoff denken, dessen Wärmekapazität kleiner als Null ist, stoßen wir auf einen Widerspruch zu unseren grundlegenden Vorstellungen von Wärme und Temperatur: Wenn \(q>0\) und \({q}/{\Delta T}<0\), muss \(\Delta T<0\) gelten, d.h. die Erwärmung des Stoffes führt zu einer Abnahme seiner Temperatur. Kurz gesagt, die von uns entwickelte Theorie enthält Prämissen, die \(C_P>0\) für jedes System erfordern, an dem wir Messungen vornehmen können.
Beschreiben wir ein Reinstoffsystem durch seinen Druck und seine Temperatur und betrachten wir reversible Prozesse mit konstantem Druck, bei denen nur Druck-Volumen-Arbeit möglich ist. Dann ist \({\left({\partial S}/{\partial T}\right)}_P={C_P}/{T}\) und \(dS={C_PdT}/{T}\). Wir wollen nun zeigen: Die Lewis- und Randall-Bedingung, dass die Entropie immer endlich ist, erfordert, dass die Wärmekapazität auf Null geht, wenn die Temperatur auf Null geht. (Da wir zeigen werden, dass das dritte Gesetz Messungen am absoluten Nullpunkt verbietet, steht diese Schlussfolgerung im Einklang mit unserer Schlussfolgerung im vorherigen Abschnitt). Dass die Wärmekapazität gegen Null geht, wenn die Temperatur gegen Null geht, ergibt sich aus \(S={C_PdT}/{T}.\) Wenn \(C_P\) nicht gegen Null geht, wenn die Temperatur gegen Null geht, wird \(dS\) beliebig groß, wenn die Temperatur gegen Null geht, was der Aussage von Lewis und Randall widerspricht.
Um dieses Ergebnis expliziter zu entwickeln, lassen wir die Wärmekapazitäten bei den Temperaturen \(T\) und Null \(C_P\left(T\right)\) bzw. \(C_P\left(0\right)\) sein. Da \(C_P\left(T\right)>0\) für jedes \(T\ >\ 0\) ist, haben wir \(S\left(T\right)-S\left(T^*\right)>0\) für jedes \(T>T^*>0\). Da die Entropie immer endlich ist, \(\infty >S\left(T\right)-S\left(T^*\right)>0\), so dass
\\ }>0\]
und
\
Für Temperaturen in der Nähe von Null, können wir die Wärmekapazität mit beliebiger Genauigkeit als Taylorreihenpolynom in \(T\) expandieren:
\
Die Ungleichungen werden zu
\
Die Bedingung auf der linken Seite erfordert \(C_P\links(0\rechts)=0\).
Wir könnten das dritte Gesetz als eine Aussage über die Wärmekapazitäten von reinen Stoffen betrachten. Wir folgern nicht nur, dass \(C_P>0\) für alle \(T>0\), sondern auch, dass
\
Allgemeiner können wir entsprechende Aussagen für geschlossene reversible Systeme ableiten, die keine reinen Stoffe sind: \({\left({\partial H}/{\partial T}\right)}_P>0\) für alle \(T>0\), und \({\mathop{\mathrm{lim}}_{T\to 0} T^{-1}{\left({\partial H}/{\partial T}\right)}_P=0\ }\). (Die Null-Temperatur-Entropien solcher Systeme sind jedoch nicht Null.) In der folgenden Diskussion beschreiben wir das System als reine Substanz. Wir können im Wesentlichen die gleichen Argumente für jedes beliebige System anführen; wir müssen nur \(C_P\) durch \({\left({\partial H}/{\partial T}\right)}_P\) ersetzen. Die Aussage von Lewis und Randall besagt, dass die Entropie am absoluten Nullpunkt konstant ist, unabhängig von den Werten anderer thermodynamischer Funktionen. Daraus folgt, dass die Entropie bei null Grad unabhängig vom Wert des Drucks ist. Für zwei beliebige Drücke, \(P_1\) und \(P_2\), gilt \(S\left(P_2,0\right)-S\left(P_1,0\right)=0\). Mit \({P=P}_1\) und \(P_2=P+\Delta P\) und haben wir
\
für jedes \(\Delta P\). Daher haben wir
\
In Kapitel 10 finden wir \({\left({\partial S}/{\partial }P\right)}_T=-{\left({\partial V}/{\partial T}\right)}_P\), also nähern sich sowohl die Entropie als auch das Volumen asymptotisch ihren Werten bei Nulltemperatur.
Wenn wir sagen, dass der absolute Nullpunkt unerreichbar ist, meinen wir damit, dass kein System eine Veränderung erfahren kann, bei der seine Endtemperatur Null ist. Um zu sehen, warum der absolute Nullpunkt unerreichbar sein muss, betrachten wir Prozesse, die die Temperatur eines Systems verringern können. Im Allgemeinen haben wir Wärmereservoirs mit verschiedenen Temperaturen zur Verfügung. Wir können das verfügbare Reservoir auswählen, dessen Temperatur am niedrigsten ist, und das System durch einfachen Wärmekontakt auf diese Temperatur bringen. So viel ist trivial; die Herausforderung besteht natürlich darin, die Temperatur weiter zu senken. Um dies zu erreichen, müssen wir eine andere Änderung vornehmen. Was auch immer diese Veränderung sein mag, sie kann nicht durch einen Wärmeaustausch mit der Umgebung unterstützt werden. Sobald wir das System auf die Temperatur des kältesten verfügbaren Teils der Umgebung gebracht haben, kann jeder weitere Wärmeaustausch mit der Umgebung nur kontraproduktiv sein. Daraus schließen wir, dass jeder für unseren Zweck geeignete Prozess adiabatisch sein muss. Da ein adiabatischer Prozess keine Wärme mit der Umgebung austauscht, \(\Delta \hat{S}=0\).
Der Prozess muss auch ein möglicher Prozess sein, so dass \(\Delta S+\Delta \hat{S}\ge 0\), und da er adiabatisch ist, \(\Delta S\ge 0\). Betrachten wir einen reversiblen Prozess und einen irreversiblen Prozess, bei dem dasselbe System von dem durch \(P_1\) und \(T_1\) spezifizierten Zustand in einen zweiten Zustand übergeht, in dem der Druck \(P_2\) ist. Die Endtemperaturen und Entropieänderungen dieser Prozesse sind unterschiedlich. Für den reversiblen Prozess ist \(\Delta S=0\); wir bezeichnen die Endtemperatur als \(T_2\). Für den irreversiblen Prozess ist \(\Delta S>0\); wir bezeichnen die Endtemperatur als \(T^*_2\). Wie sich herausstellt, ist die Temperaturänderung für den irreversiblen Prozess geringer als für den reversiblen Prozess, d. h. \(T_2-T_1<t^*_2-t_1\)>. Äquivalent dazu erreicht der reversible Prozess eine niedrigere Temperatur: \({T_2<t}^*_2\)>. Aus
\
können wir die Entropieänderungen für diese Prozesse berechnen. Für den reversiblen Prozess berechnen wir \
Dazu berechnen wir zunächst
\
für die isotherme reversible Umwandlung vom Zustand \(P_1\), \(T_1\) in den durch \(P_2\) und \(T_1\) angegebenen Zustand. Für diesen Schritt ist \(dT\) gleich Null, so dass
\
Wir berechnen dann
\
für die isobare reversible Transformation vom Zustand \(P_2\), \(T_1\) zum Zustand \(P_2\), \(T_2\). Für diese Umwandlung ist \(dP\) Null, und
\
Dann,
\
Da \(\Delta S^{rev}=0\), ist der reversible Prozess eindeutig, d.h. bei \(P_1\), \(T_1\) und \(P_2\) ist die Endtemperatur des Systems bestimmt. Wir finden \(T_2\) aus
\
Um die Entropieänderung für den irreversiblen Prozess zu verstehen, stellen wir zunächst fest, dass es eine unendliche Anzahl solcher Prozesse gibt. Es gibt nichts Einzigartiges an der Endtemperatur. Bei gegebenen Werten \(P_1\), \(T_1\) und \(P_2\) kann die Endtemperatur \(T^*_2\) jeden Wert annehmen, der mit den Eigenschaften des Stoffes vereinbar ist. Um einen bestimmten irreversiblen Prozess zu beschreiben, müssen wir alle vier Größen \(P_1\), \(T_1\), \(P_2\) und \(T^*_2\) angeben. Danach können wir jedoch die Entropieänderung für den irreversiblen Prozess berechnen,
\
, indem wir die Entropieänderungen berechnen, während wir das System reversibel entlang des isothermen Zweischrittpfades von \(P_1\), \(T_1\) zu \(P_2\), \(T_1\) und dann entlang des isobaren Pfades von \(P_2\), \(T_1\) zu \(P_2\), \(T^*_2\). Die Berechnung von \(\Delta S^{irrev}\) für diesen reversiblen Pfad von \(P_1\), \(T_1\) nach \(P_2\), \(T^*_2\) erfolgt nach derselben Logik wie die Berechnung von \(\Delta S\) für den reversiblen Pfad von \(P_1\), \(T_1\) nach \(P_2\), \(T_2\) im vorigen Absatz. Der Unterschied besteht darin, dass \(T^*_2\) als obere Grenze des Temperaturintegrals durch \(T_2\) ersetzt wird. Das Druckintegral ist das gleiche. Wir haben
\
Aus \(\Delta S^{irrev}>\Delta S^{rev}\) haben wir
\
Da die Integrale gleich und positiv sind, folgt daraus, dass \(T^*_2>T_2\), wie oben behauptet.
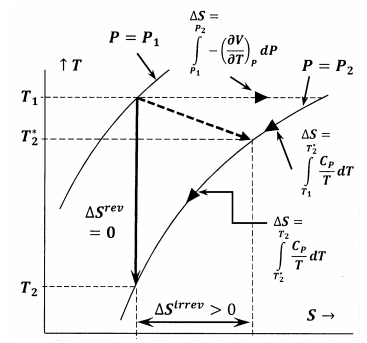
Abbildung 6 zeigt die Beziehungen zwischen den verschiedenen Größen, die in diesem Argument diskutiert werden. Zunächst zeigt Abbildung 6 eine Darstellung von zwei Isobaren des Systems im Temperatur-Entropie-Raum. Das heißt, die Linie mit der Beschriftung \(P=P_1\) stellt die Menge der Temperatur-Entropie-Punkte dar, an denen das im Gleichgewicht befindliche System den Druck \(P_1\) hat; die Linie mit der Beschriftung \(P=P_2\) stellt die Gleichgewichtspositionen bei Druck \(P_2\) dar. Andere Linien in dieser Skizze stellen Pfade dar, entlang derer das System bei konstanter Entropie oder konstanter Temperatur reversible Veränderungen erfahren kann. Die gepunktete Linie stellt den irreversiblen Prozess dar, bei dem das System von dem durch \(P_1\), \(T_1\) angegebenen Zustand in den durch \(P_2\), \(T^*_2\) angegebenen Zustand übergeht. Diese Linie ist gestrichelt, um die Tatsache darzustellen, dass die Temperatur des Systems während des irreversiblen Prozesses möglicherweise nicht genau definiert ist.
Eine wirksame Kühlung kann durch Druckänderungen erreicht werden, wenn das System ein Gas ist. Bei Flüssigkeiten und Festkörpern ist jedoch \({\left({\partial V}/{\partial T}\right)}_P\) klein; folglich ist auch die Temperaturänderung bei einer reversiblen Druckänderung klein. Bei Temperaturen nahe dem absoluten Nullpunkt sind fast alle Stoffe fest; um eine wirksame Kühlung zu erreichen, müssen wir eine thermodynamische Variable ändern, für die der Temperaturkoeffizient eines Festkörpers so groß wie möglich ist. Um das allgemeine Problem der Senkung der Temperatur eines Systems durch Veränderung einer anderen Größe als des Drucks zu betrachten, müssen wir ein System betrachten, in dem irgendeine Form von Arbeit möglich ist, die nicht dem Druck oder dem Volumen entspricht. Ein solches System unterliegt einer zusätzlichen Kraft, und seine Energie ändert sich, wenn sich diese Kraft ändert.
Adiabatische Entmagnetisierung
Die praktische Methode, mit der extrem niedrige Temperaturen erreicht werden, heißt adiabatische Entmagnetisierung. Diese Methode nutzt die Eigenschaften paramagnetischer Festkörper aus. In solchen Festkörpern erzeugen ungepaarte Elektronen, die auf einzelnen Atomen lokalisiert sind, ein magnetisches Moment. Die Quantenmechanik führt zu wichtigen Schlussfolgerungen über die Wechselwirkung zwischen solchen magnetischen Momenten und einem angelegten Magnetfeld: In einem angelegten Magnetfeld ist das magnetische Moment eines einzelnen Atoms quantisiert. Im einfachsten Fall kann es nur in zwei Richtungen ausgerichtet werden; es muss entweder parallel oder antiparallel zum angelegten Magnetfeld liegen. Wenn das magnetische Moment eines Atoms parallel zum Magnetfeld ausgerichtet ist, ist die Energie des Systems geringer als bei einer antiparallelen Ausrichtung. Das angelegte Magnetfeld übt eine Kraft auf die mit den einzelnen Atomen verbundenen magnetischen Momente aus. Die Energie des Systems hängt von der Stärke des angelegten Magnetfelds ab.
Anstatt sich auf den besonderen Fall der adiabatischen Entmagnetisierung zu konzentrieren, betrachten wir die Energie- und Entropieänderungen, die mit Änderungen eines verallgemeinerten Potenzials (\(\mathit{\Phi}}_{\theta }\) und seiner verallgemeinerten Verschiebung (\(\theta\)) einhergehen. (Bei adiabatischer Entmagnetisierung wäre \(\theta\) das angelegte Magnetfeld). Um reversible Veränderungen in diesem System zu beschreiben, sind drei Variablen erforderlich. Wir können die Energie und Entropie als Funktionen von Temperatur, Druck und \(\theta\) ausdrücken:
\(E=E\links(T,P,\theta \rechts)\) und \(S=S\links(T,P,\theta \rechts)\). Das Gesamtdifferential der Entropie enthält einen Term, der die Abhängigkeit der Entropie von \(\theta\) angibt. Wir haben
\
wobei wir \(C\left(T,P,\theta \right)\) schreiben, um zu betonen, dass wir für unsere Zwecke jetzt die Wärmekapazität bei konstantem Druck und konstantem \(\theta\) messen müssen.
Bei konstantem Druck P und konstanter Verdrängung \(\theta\) hängt die Entropie von der Temperatur ab wie
\
Das Postulat, dass die Entropie bei jeder Temperatur endlich ist, impliziert, dass die druck- und \(\theta\)-abhängige Wärmekapazität am absoluten Nullpunkt Null wird. Das heißt, am absoluten Nullpunkt verschwindet die Wärmekapazität unabhängig von den Werten von P und \(\theta\). Die Argumentation ist genau dieselbe wie zuvor. Zuvor hatten wir \(C_P\links(0\rechts)=0\) geschrieben; für den vorliegenden verallgemeinerten Fall schreiben wir \(C\links(0,P,\theta \rechts)=0\).
Aus dem Postulat, dass die Entropie bei absolutem Nullpunkt für alle Werte der anderen thermodynamischen Variablen konstant ist, folgt, dass für zwei beliebige Drücke \(P_1\) und \(P_2\) und für zwei beliebige Werte der verallgemeinerten Verschiebung, \(P_1\) und \(P_2\),
\
und somit, dass
\ und \
Wir wollen einen Prozess betrachten, bei dem ein System von der niedrigsten in der Umgebung verfügbaren Temperatur zu einer noch niedrigeren Temperatur übergeht. Um die Endtemperatur zu minimieren, muss dieser Prozess adiabatisch durchgeführt werden. Außerdem muss es sich um einen möglichen Prozess handeln, so dass \(dS\ge 0\). Der Einfachheit halber nehmen wir nun an, dass wir diesen Prozess bei einem konstanten Druck, \(P\), durchführen und dass das System von dem durch \(P\), \(T_1\), \(T_1\) spezifizierten Zustand in den durch \(P\), \(T_2\), \(T_2\) spezifizierten Zustand übergeht, wobei \(T_1>T_2\). Die Entropien dieser beiden Zustände sind
\ und \
Die Entropieänderung für diesen Prozess ist
\ \
Nehmen wir nun an, dass die Endtemperatur Null ist; das heißt, \(T_2=0\), so dass
\ Daraus folgt, dass \
wobei die Ungleichung auf der rechten Seite aus der Tatsache folgt, dass \(C\left(T,P,{\theta }_1\right)>0\). Daraus folgt, dass
\
, was der Aussage von Lewis und Randall zum dritten Gesetz widerspricht. Die Annahme, dass das System den absoluten Nullpunkt erreichen kann, führt zu einem Widerspruch zur Lewis-Randall-Aussage des dritten Gesetzes. Wenn also die Lewis-Randall-Aussage wahr ist, ist der absolute Nullpunkt unerreichbar.
Das Umgekehrte gilt auch, d.h. aus dem Satz, dass der absolute Nullpunkt unerreichbar ist, können wir zeigen, dass die Lewis-Randall-Aussage wahr ist. Dazu ordnen wir die obige Gleichung für \(\Delta S\),
\ \
Wenn wir nun annehmen, dass die Lewis-Randall-Aussage falsch ist, kann der Ausdruck auf der rechten Seite kleiner oder gleich Null sein. Das Integral auf der linken Seite kann dann gleich Null sein, so dass das System den absoluten Nullpunkt erreichen kann. Wenn die Aussage von Lewis und Randall falsch ist, ist es wahr, dass das System den absoluten Nullpunkt erreichen kann. Daraus folgt: Wenn das System den absoluten Nullpunkt nicht erreichen kann, ist die Lewis- und Randall-Aussage wahr.
Die Abbildungen 7 und 8 veranschaulichen diese Ideen anhand von Konturdiagrammen im Temperatur-Entropie-Raum. Jede Abbildung zeigt zwei Konturlinien. Eine dieser Konturlinien ist eine Reihe von Temperatur- und Entropiewerten, entlang derer der Druck konstant bei \(P\) und \(\theta\) konstant bei \({\theta }_1\) ist. Die andere Konturlinie ist eine Reihe von Temperatur- und Entropiewerten, entlang derer der Druck bei \(P\) und \(\theta\) bei \({\theta }_2\) konstant ist. Die Steigung einer Konturlinie ist
\
Da die Wärmekapazität immer positiv ist, ist diese Steigung immer positiv.
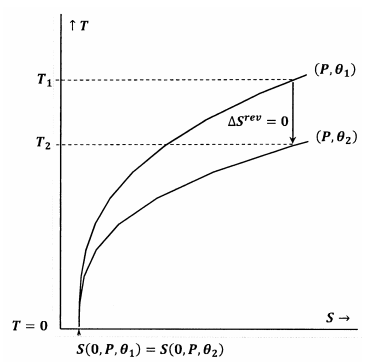
In Abbildung 7 ist die Lewis-Randall-Aussage erfüllt. Wenn die Temperatur gegen Null geht, treffen sich die Konturlinien bei demselben Wert der Entropie; diese Konturen erfüllen die Beziehung
\
Ein adiabatischer (vertikaler) Pfad von der Kontur für \(P\) und \({\theta }_1\) trifft die Kontur für \(P\) und \({\theta }_2\) bei einer positiven Temperatur, \(T_2>0\). Da dies offensichtlich für jedes \(P\) und jedes \({\theta }_2\) gilt, wird der Endzustand für jeden adiabatischen Prozess \(T_2>0\) haben. Da die Lewis-Randall-Aussage erfüllt ist, kann das System den absoluten Nullpunkt nicht erreichen und umgekehrt.
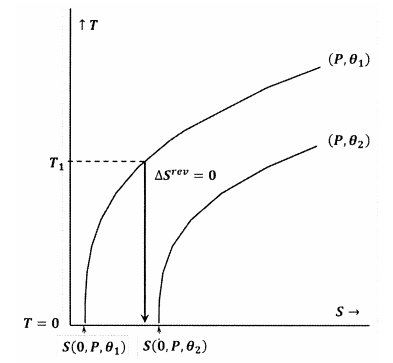
In Abbildung 8 ist die Lewis-Randall-Aussage verletzt, weil wir \(S\left(0,P,{\theta }_1\right)\) haben. In diesem Fall wird ein adiabatischer Prozess, der von einer ausreichend niedrigen Anfangstemperatur \(T_1\) ausgeht, den absoluten Nullpunkt erreichen, ohne die Kontur für die Konstanten \(P\) und \({\theta }_2\) zu schneiden. Da die Lewis-Randal-Aussage verletzt wird, kann das System den absoluten Nullpunkt erreichen und umgekehrt.