1D & 3D Convolutions explained with… MS Excel!

Wir haben im ersten Beitrag mit 2D Convolutions begonnen, weil Convolutions nach den Erfolgen im Bereich der Computer Vision an Popularität gewonnen haben. Da Aufgaben in diesem Bereich Bilder als Eingaben verwenden und natürliche Bilder in der Regel Muster entlang zweier räumlicher Dimensionen (Höhe und Breite) aufweisen, sieht man häufiger Beispiele für 2D-Konvolutionen als für 1D- und 3D-Konvolutionen.

In jüngster Zeit gab es jedoch eine große Anzahl von Erfolgen bei der Anwendung von Konvolutionen auch auf Aufgaben der Verarbeitung natürlicher Sprache. Da Aufgaben in diesem Bereich Text als Input verwenden und Text Muster entlang einer einzigen räumlichen Dimension (d.h. Zeit) aufweist, sind 1D-Convolutions eine hervorragende Lösung! Wir können sie als effizientere Alternative zu traditionellen rekurrenten neuronalen Netzen (RNNs) wie LSTMs und GRUs verwenden. Im Gegensatz zu RNNs können sie für wirklich schnelle Berechnungen parallel ausgeführt werden.

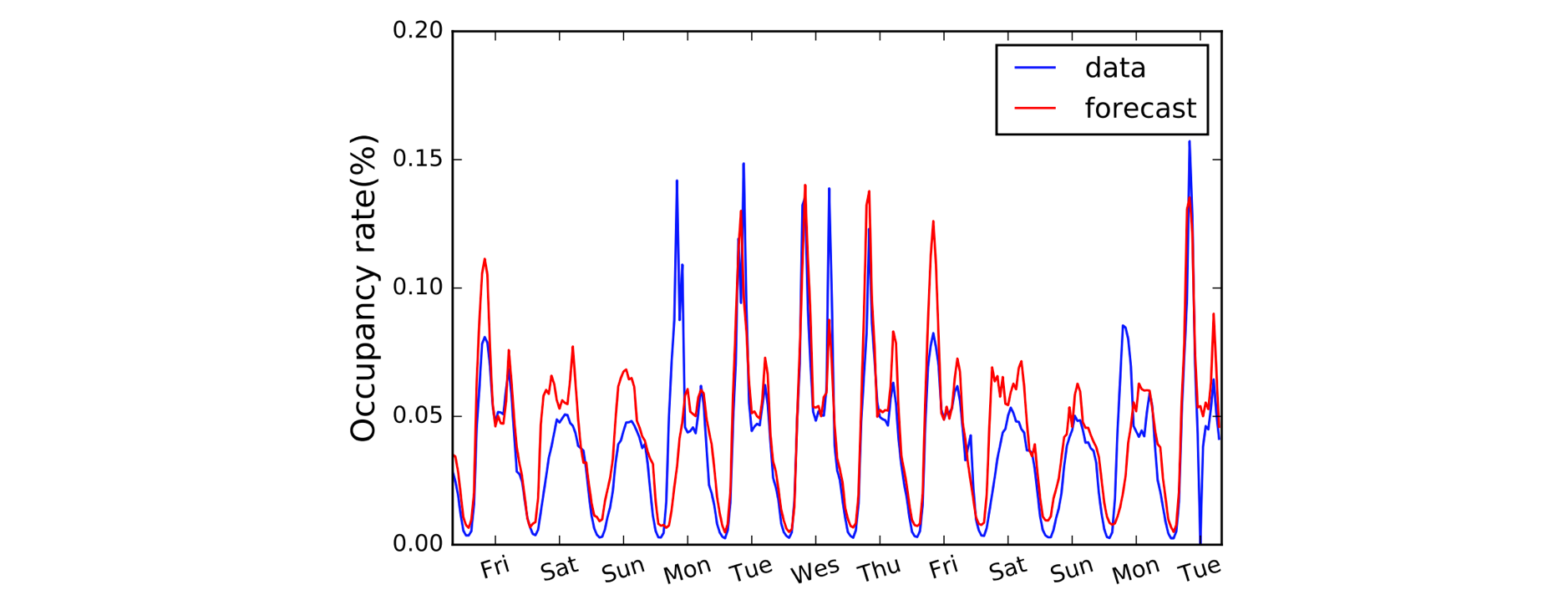
Ein weiterer Bereich, der von 1D Convolutions profitiert, ist die Modellierung von Zeitreihen. Wie zuvor haben wir eine einzige räumliche Dimension in unseren Eingabedaten (d.h. die Zeit), und wir wollen Muster über Zeiträume hinweg erkennen. Wir nennen diese Art von Daten oft „sequenziell“, weil sie als eine Folge von Werten betrachtet werden können. Und die räumliche Dimension wird oft als „zeitliche“ Dimension bezeichnet. Die Verwendung von 1D-Convolutions vor RNNs ist ebenfalls weit verbreitet: Das LSTNet-Modell ist ein Beispiel dafür, und seine Vorhersagen für die Verkehrsprognose sind unten dargestellt.

A, B, C. Es ist ganz einfach: (1,3,3) Punkt (2,0,1) = 5.

Nachdem die Namenskonventionen geklärt sind, wollen wir uns nun die Arithmetik genauer ansehen. Wir haben Glück, denn 1D-Faltungen sind eigentlich nur eine vereinfachte Version der 2D-Faltung!

Bei der Berechnung eines einzelnen Ausgabewerts können wir unseren Kernel der Größe 3 auf den gleich großen Bereich auf der linken Seite unserer Eingabematrix anwenden. Wir berechnen das „Punktprodukt“ der Eingaberegion und des Kernels, was, um es noch einmal zusammenzufassen, einfach das elementweise Produkt ist (d.h. wir multiplizieren die Farbpaare), gefolgt von einer globalen Summe, um einen einzigen Wert zu erhalten. In diesem Fall also:

(1*2) + (3*0) + (3*1) = 5

Wir wenden dieselbe Operation (mit demselben Kernel) auf die anderen Regionen des Eingabefeldes an, um das vollständige Ausgabefeld (5,6,7,2) zu erhalten; d. h. wir schieben den Kernel über das gesamte Eingabefeld. Anders als bei 2D-Faltungen, bei denen wir den Kernel in zwei Richtungen verschieben, verschieben wir ihn bei 1D-Faltungen nur in eine Richtung, in diesem Diagramm nach links/rechts.

Erweitert: Eine 1D-Faltung ist nicht dasselbe wie eine 1×1 2D-Faltung.

Codierung

Überraschenderweise benötigen wir für unsere 1D-Faltung einen Conv1D-Block in Gluon. Wir definieren die Kernelform als 3, und da wir in diesem Beispiel nur mit einem einzigen Kernel arbeiten, geben wir channels=1 an.

import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)

Wir können nun unsere Eingaben in den conv-Block mit einem vordefinierten Kernel eingeben.

input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>

Was ändert sich mit Padding, Stride und Dilatation?

Wir haben die Auswirkungen von Padding, Stride und Dilatation im letzten Beitrag über 2D-Konvolutionen gesehen, und es ist sehr ähnlich für 1D-Konvolutionen. Beim Auffüllen wird diesmal nur entlang einer einzigen Dimension (der zeitlichen Dimension) aufgefüllt. Unser Diagramm stellt die Zeit auf der horizontalen Achse dar, so dass wir links und rechts von den Eingabedaten auffüllen (und nicht oben und unten wie im Beispiel der 2D-Faltung). Bei Stride und Dilatation wenden wir sie ebenfalls nur entlang der zeitlichen Dimension an. Ein Beispiel mit Padding und Stride würde also wie folgt aussehen:

Wir fügen zwei zusätzliche Argumente in den Code ein: padding=1 und strides=2.

conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>

Erweitert: Die Abmessungen der Eingabedaten müssen einer bestimmten Reihenfolge entsprechen, die als Layout bezeichnet wird. Standardmäßig erwartet die 1D-Faltung, dass sie auf Eingabedaten des Formats „NCW“ angewendet wird, d. h. Losgröße (N) * Kanäle (C) * Breite/Zeit (W). Und für 2D-Faltungen ist die Vorgabe NCHW, d. h. Stapelgröße (N) * Kanäle (C) * Höhe (H) * Breite (W). Prüfen Sie das layout-Argument von Conv1D und Conv2D.