3D-Rekonstruktion

In dieser Übung geht es darum, die notwendige Logik zu programmieren, damit der Kobuki-Roboter eine 3D-Rekonstruktion der Szene erstellen kann, die er über seine linke und rechte Kamera empfängt.

Installation

Installation der allgemeinen Infrastruktur der JdeRobot Robotics Academy.

Wie wird die Lösung ausgeführt?

Navigiere zum 3d_reconstruction Verzeichnis

cd exercises/3d_reconstruction

Starte Gazebo mit der kobuki_3d_reconstruction Welt über den Befehl

roslaunch ./launch/3d_reconstruction_ros.launch

Dann musst du die akademische Anwendung ausführen, die deinen Code enthält:

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

Wie wird die Übung ausgeführt?

Um die Übung durchzuführen, müssen Sie die Datei MyAlgorithm.py bearbeiten und darin Ihren Code einfügen, der 3D-Punkte aus den beiden Stereoansichten rekonstruiert.

Wo fügen Sie den Code ein?

In die Datei MyAlgorithm.py,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Anwendungsprogrammierschnittstelle

• self.getImage('left') – um das linke Bild zu erhalten
• self.getImage('right') – um das rechte Bild zu erhalten
• self.point.PlotPoint(position, color) – um den Punkt im 3D-Werkzeug zu zeichnen

Navigieren in der GUI-Schnittstelle

Mausbasiert: Halten und ziehen, um sich in der Umgebung zu bewegen. Scrollen zum Vergrößern oder Verkleinern

Tastaturbasiert: Pfeiltasten, um sich in der Umgebung zu bewegen. W- und S-Tasten zum Vergrößern oder Verkleinern

Theorie

In der Computer Vision und Computergrafik ist die 3D-Rekonstruktion der Prozess der Bestimmung des 3D-Profils eines Objekts sowie der Kenntnis der 3D-Koordinaten eines beliebigen Punktes auf dem Profil. Die Rekonstruktion kann auf folgende Weise erfolgen:

• Hardwarebasiert: Der hardwarebasierte Ansatz erfordert die Verwendung der für die Rekonstruktionsaufgabe spezifischen Hardware. Beispiele hierfür sind strukturiertes Licht, Laserentfernungsmesser, Tiefenmesser und radiometrische Methoden.

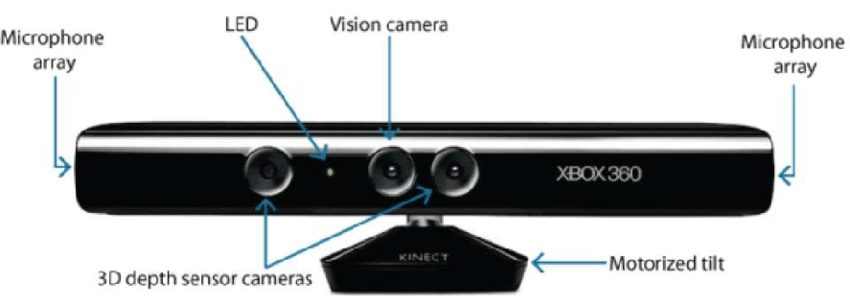
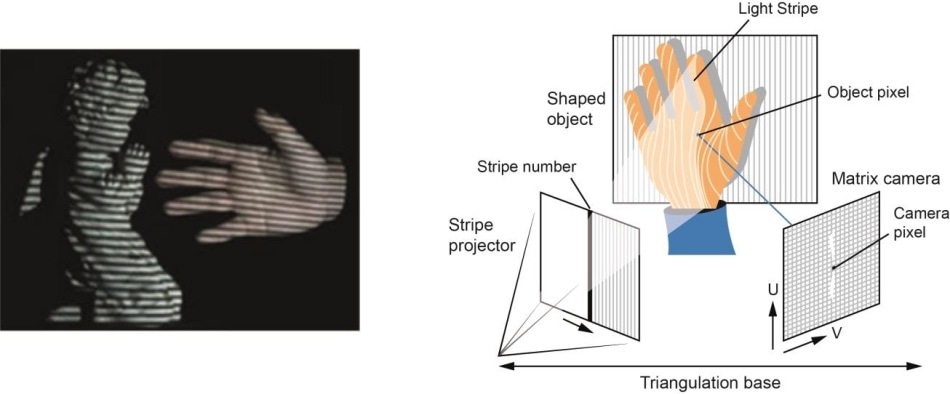
• Softwarebasiert: Der softwarebasierte Ansatz stützt sich auf die Berechnungsfähigkeiten des Computers, um die 3D-Eigenschaften des Objekts zu bestimmen. Form aus Schattierung, Textur, Stereovision und Homographie sind einige gute Methoden.

In dieser Übung besteht unser Hauptziel darin, eine 3D-Rekonstruktion mit Hilfe eines softwarebasierten Ansatzes durchzuführen, insbesondere eine 3D-Rekonstruktion mit Stereovision.

Epipolare Geometrie

Wenn zwei Kameras eine 3D-Szene von zwei verschiedenen Positionen aus betrachten, gibt es eine Reihe von geometrischen Beziehungen zwischen den 3D-Punkten und ihren Projektionen auf die 2D-Bilder, die zu Einschränkungen zwischen den Bildpunkten führen. Die Untersuchung dieser Eigenschaften und Beschränkungen wird als Epipolargeometrie bezeichnet. Die folgende Abbildung und Erläuterung kann die Idee verallgemeinern:

Angenommen, ein Punkt X im 3D-Raum wird in zwei Ansichten abgebildet, bei x in der ersten und x' in der zweiten. Projiziert man die Strahlen durch die Bildebenen auf ihre Kamerazentren zurück, so erhält man eine ebene Fläche, die mit π bezeichnet wird.

Angenommen, wir kennen nur x, so stellt sich die Frage, wie der entsprechende Punkt x' eingegrenzt wird. Die Ebene π wird durch die Grundlinie (Verbindungslinie zwischen den Kamerazentren) und den durch x definierten Strahl bestimmt. Von oben wissen wir, dass der Strahl, der dem unbekannten Punkt x' entspricht, in π liegt, daher liegt der Punkt x' auf der Schnittlinie l' von π mit der zweiten Bildebene. Diese Linie wird die Epipolarlinie genannt, die x entspricht. Diese Beziehung hilft uns, den Suchraum des Punktes im rechten Bild von einer Ebene auf eine Linie zu reduzieren. Einige wichtige Definitionen sind:

• Der Epipol ist der Schnittpunkt der Linie, die die Kameramittelpunkte (die Grundlinie) mit der Bildebene verbindet.

• Eine Epipolarebene ist eine Ebene, die die Grundlinie enthält.

• Eine Epipolarlinie ist der Schnittpunkt der Epipolarebene mit der Bildebene.

Stereo-Rekonstruktion

Die Stereo-Rekonstruktion ist ein Spezialfall der obigen 3D-Rekonstruktion, bei der die beiden Bildebenen parallel zueinander und gleich weit von dem 3D-Punkt entfernt sind, den wir darstellen wollen.

In diesem Fall ist die Epipolarlinie für beide Bildebenen gleich und verläuft parallel zur Breite der Ebenen, was unsere Einschränkung vereinfacht.

3D-Rekonstruktionsalgorithmus

Der Rekonstruktionsalgorithmus besteht aus 3 Schritten:

1. Erkennen der Merkmalspunkte in einer Bildebene
2. Erkennen des Merkmalspunktes, der dem oben gefundenen Punkt entspricht
3. Triangulieren des Punktes im 3D-Raum

Schauen wir sie uns einzeln an

Erkennung von Merkmalspunkten

Die Erkennung von Merkmalspunkten ist ein weites Feld, auf dem bereits mehrere Algorithmen untersucht werden. Die Algorithmen Harris Corner Detection und Shi-Tomasi verwenden Eigenwerte, um einen guten Merkmalspunkt zu finden. Das Problem ist jedoch, dass wir viele Punkte für die 3D-Rekonstruktion benötigen und diese Algorithmen nicht in der Lage sind, uns eine so große Anzahl von Merkmalspunkten zu liefern.

Daher verwenden wir Kantenpunkte als Merkmalspunkte. In der nächsten Phase des Algorithmus kann es zu Mehrdeutigkeiten bei ihrer Erkennung kommen. Aber unser Problem ist gelöst, wenn wir Kanten als Merkmalspunkte verwenden. Ein wirklich cooler Kantendetektor ist der Canny Edge Detection Algorithmus. Der Algorithmus ist recht einfach und zuverlässig in Bezug auf die Erzeugung von Kanten.

Feature Point Extraction

Die Verwendung der epipolaren Beschränkung vereinfacht die Zeitkomplexität unseres Algorithmus. Bei allgemeinen 3D-Rekonstruktionsproblemen müssen wir für jeden Punkt in einem Bild eine epipolare Linie erzeugen und dann in diesem Musterraum den entsprechenden Punkt im anderen Bild suchen. Die Erzeugung der Epipolarlinie ist auch in unserem Fall sehr einfach, es handelt sich lediglich um die Iterpolation einer parallelen Linie von der linken zur rechten Bildebene.

Die Überprüfung der Übereinstimmung zwischen den Bildern beinhaltet viele Algorithmen, wie die Summe der quadratischen Differenzen oder die Energieminimierung. Ohne zu sehr in die Tiefe zu gehen, reicht für unseren Anwendungsfall auch die Verwendung eines einfachen Korrelationsfilters.

Triangulation

Triangulation bedeutet einfach ausgedrückt, dass man anhand der beiden ermittelten Punkte in den Bildebenen berechnet, wo der 3D-Punkt liegen wird.

In der Realität kann die Position der Bildpunkte nicht exakt gemessen werden. Bei allgemeinen Kameras kann es zu geometrischen oder physikalischen Verzerrungen kommen. Daher steckt eine Menge Mathematik dahinter, diesen Fehler zu minimieren und die genaueste 3D-Punktprojektion zu berechnen. Unter diesem Link finden Sie ein einfaches Modell.

Hinweise

Einfache Hinweise, die Ihnen bei der Lösung der Übung 3d_reconstruction helfen. Die OpenCV-Bibliothek wird für diese Übung ausgiebig genutzt.

Setup

Mit Hilfe der Übungs-API können wir die Bilder leicht abrufen. Nachdem wir die Bilder erhalten haben, ist es eine gute Idee, eine bilaterale Filterung der Bilder durchzuführen, da es einige zusätzliche Details gibt, die bei der 3D-Rekonstruktion nicht berücksichtigt werden müssen. Schauen Sie sich die Abbildungen an, um die Auswirkungen der bilateralen Filterung zu sehen.

Korrespondenzberechnung

OpenCV hat bereits eingebaute Korrelationsfilter, die über matchTemplate() aufgerufen werden können. Achten Sie auf Extremfälle wie Kanten und Ecken.

Eine gute Beobachtung ist, dass die Punkte auf der linken Seite eine Korrespondenz im linken Teil und die Punkte auf der rechten Seite eine Korrespondenz im rechten Teil haben werden. Mit dieser Beobachtung können wir die Berechnung der Korrespondenz leicht beschleunigen.

Darstellung der Punkte

Eine manuelle oder OpenCV-basierte Funktion triangulatePoints funktioniert gut für die Triangulation. Achten Sie bei der algebraischen Umsetzung einfach auf alle Matrixformen und -größen.

Beachten Sie den Unterschied zwischen einfachen 3D-Koordinaten und homogenen 4D-Koordinaten. Schauen Sie sich dieses Video für Details an. Durch einfache Division des kompletten 4D-Vektors durch seine 4. Koordinate erhält man die 3D-Koordinaten.

Aufgrund der unterschiedlichen Implementierungen der Benutzer muss der Benutzer möglicherweise den Maßstab und den Versatz der triangulierten Punkte anpassen, um sie in der GUI-Schnittstelle sichtbar und darstellbar zu machen. Die Verkleinerung des 3D-Koordinatenvektors um einen Wert zwischen 500 und 1000 funktioniert gut. Auch ein Offset von 0 bis 8 funktioniert gut.

Abbildungen