Definition der Säurekonstante
Sie wissen zweifellos, dass einige Säuren stärker sind als andere. Die relative Säurestärke verschiedener Verbindungen oder funktioneller Gruppen – mit anderen Worten, ihre relative Fähigkeit, unter gleichen Bedingungen ein Proton an eine gemeinsame Base abzugeben – wird durch eine Zahl quantifiziert, die Säurekonstante, abgekürzt \(K_a\). Die zum Vergleich gewählte gemeinsame Base ist Wasser.
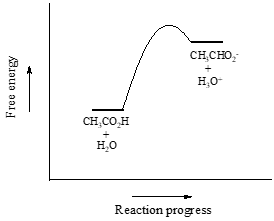
Als erstes Beispiel betrachten wir Essigsäure. Wenn wir eine verdünnte Lösung von Essigsäure in Wasser herstellen, kommt es zu einer Säure-Base-Reaktion zwischen der Säure (Protonendonator) und Wasser (Protonenakzeptor).

Essigsäure ist eine schwache Säure, so dass das Gleichgewicht die Reaktanten gegenüber den Produkten begünstigt – es ist thermodynamisch „bergauf“. Dies wird in der obigen Abbildung durch die relative Länge der Vorwärts- und Rückwärtsreaktionspfeile angedeutet.
Die Gleichgewichtskonstante \(K_{eq}\) ist definiert als:
\}{} = \frac{}{}\]
Denken Sie daran, dass es sich um eine verdünnte wässrige Lösung handelt: Wir haben eine kleine Menge Essigsäure zu einer großen Menge Wasser gegeben. Daher ändert sich die Konzentration des Wassers (ca. 55,6 mol/L) im Laufe der Reaktion nur wenig und kann als konstant betrachtet werden.
Verschiebt man den konstanten Term für die Wasserkonzentration auf die linke Seite des Ausdrucks für die Gleichgewichtskonstante, erhält man den Ausdruck für \(K_a\), die Säurekonstante für Essigsäure:
\ = \frac{}{}\]
Allgemeiner ausgedrückt, wird die Dissoziationskonstante für eine gegebene Säure HA oder HB+ wie folgt ausgedrückt:
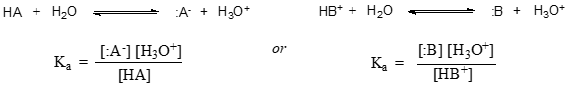
Der Wert von \(K_a\) für Essigsäure ist \(1.75 \mal 10^{-5}\) – viel weniger als \(1\), was darauf hinweist, dass im Gleichgewicht viel mehr Essigsäure in Lösung ist als Acetat und Hydronium-Ionen.
Umgekehrt gehen Schwefelsäure mit einem \(K_a\) von etwa \(10^9\) oder Salzsäure mit einem \(K_a\) von etwa \(10^7\) in Wasser im Wesentlichen vollständig in Dissoziation: Sie sind sehr starke Säuren.
Eine Zahl wie \(1,75 \mal 10^{- 5}\) ist nicht sehr einfach auszusprechen, zu merken oder zu veranschaulichen, daher verwenden Chemiker gewöhnlich einen bequemeren Begriff, um die relative Säure auszudrücken. Der \(pK_a\)-Wert einer Säure ist einfach der Logarithmus (Basis 10) ihres \(K_a\)-Wertes.
\
Bei der Berechnung ergibt sich, dass der \(pK_a\)-Wert von Essigsäure \(4,8\) ist. Der \(pK_a\) von Schwefelsäure beträgt -10 und von Salzsäure -7. Die Verwendung von \(pK_a\)-Werten ermöglicht es uns, den relativen Säuregrad gängiger Verbindungen und funktioneller Gruppen auf einer numerischen Skala von etwa -10 (für eine sehr starke Säure) bis 50 (für eine Verbindung, die überhaupt nicht sauer ist) anzugeben. Je niedriger der \(pK_a\)-Wert ist, desto stärker ist die Säure.
Die ionisierbaren (Protonen abgebenden oder aufnehmenden) funktionellen Gruppen, die für die biologische organische Chemie relevant sind, haben im Allgemeinen \(pK_a\)-Werte von etwa 5 bis etwa 20. Die wichtigsten davon sind im Folgenden zusammengefasst, mit sehr groben \(pK_a\)-Werten für die konjugierten Säureformen. Weitere saure Gruppen mit \(pK_a\)-Werten nahe Null sind ebenfalls als Referenz aufgeführt.
Typische \(pK_a\) Werte
| Gruppe | ungefähre \(pK_a\) |
|---|---|
| Hydroniumion | 0 |
| protonierter Alkohol | 0 |
| protoniertes Carbonyl | 0 |
| Carbonsäuren | 5 |
| protonierte Imine | 7 |
| protonierte Amine | 10 |
| Phenole | 10 |
| Thiole | 10 |
| Alkohole, Wasser | 15 |
| \(\alpha\)-Kohlenstoffsäuren * | 20 |
*\(\alpha\)-Kohlenstoffsäuren werden in Abschnitt 7 erläutert.6A
Es ist sehr empfehlenswert, sich diese groben Werte jetzt einzuprägen – wenn Sie dann einen genaueren Wert benötigen, können Sie ihn jederzeit in einer vollständigeren \(pK_a\)-Tabelle nachschlagen. Der Anhang zu diesem Buch enthält eine detailliertere Tabelle mit typischen \(pK_a\)-Werten, und viel vollständigere Tabellen sind in Quellen wie dem Handbook of Chemistry and Physics verfügbar.
\(pK_a\) vs. \(pH\)
Es ist wichtig zu wissen, dass \(pK_a\) nicht dasselbe ist wie \(pH\): Ersteres ist eine inhärente Eigenschaft einer Verbindung oder funktionellen Gruppe, während letzteres ein Maß für die Hydroniumionenkonzentration in einer bestimmten wässrigen Lösung ist:
\\]
Die Kenntnis der \(pK_a\)-Werte ermöglicht uns nicht nur den Vergleich der Säurestärke, sondern auch den Vergleich der Basenstärke. Der wichtigste Gedanke, den man sich merken sollte, ist folgender: Je stärker die konjugierte Säure, desto schwächer die konjugierte Base. Wir können feststellen, dass das Hydroxidion eine stärkere Base ist als Ammoniak (\(NH_3\)), weil das Ammoniumion (\(NH4^+\), \(pK_a = 9.2\)) eine stärkere Säure ist als Wasser (\(pK_a = 15.7\)).
Übung \(\PageIndex{1}\)
Welche ist die stärkere Base, \(CH_3O^-\) oder \(CH_3S^-\)? Acetat-Ion oder Ammoniak? Hydroxid-Ion oder Acetat-Ion?
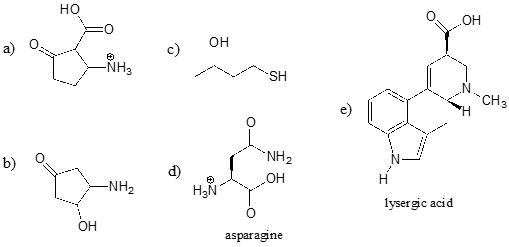
Lassen Sie uns unser Verständnis des \(pK_a\)-Konzepts im Zusammenhang mit einem komplexeren Molekül anwenden. Wie lautet zum Beispiel der \(pK_a\) der nachstehenden Verbindung?

Wir müssen den potenziellen Säuregrad von vier verschiedenen Arten von Protonen des Moleküls bewerten und die sauerste finden. Die aromatischen Protonen sind nicht alle sauer – ihr \(pK_a\) liegt bei etwa 45. Die Amingruppe ist ebenfalls nicht sauer, ihr \(pK_a\) liegt bei etwa 35. (Zur Erinnerung: ungeladene Amine sind basisch; nur positiv geladene, protonierte Amine mit \(pK_a\) Werten um 10 sind schwach sauer). Das Proton des Alkohols hat einen \(pK_a\) von etwa 15 und das Proton des Phenols einen \(pK_a\) von etwa 10: die sauerste Gruppe des obigen Moleküls ist also das Phenol (achten Sie darauf, dass Sie den Unterschied zwischen einem Phenol und einem Alkohol erkennen können – denken Sie daran, dass die \(OH\)-Gruppe in einem Phenol direkt an den aromatischen Ring gebunden ist). Wenn dieses Molekül mit einem molaren Äquivalent einer starken Base wie Natriumhydroxid reagieren würde, würde das Phenolproton zur Bildung eines Phenolatanions abgegeben werden.
Übung \(\PageIndex{2}\)
Bestimmen Sie die sauerste funktionelle Gruppe in jedem der unten aufgeführten Moleküle und geben Sie ihren ungefähren \(pK_a\) an.