Abelsche Gruppe | CDhistory

Eine abelsche Gruppe ist eine Gruppe, bei der die Elemente kommutieren (d.h. für alle Elemente und ). Abelsche Gruppen entsprechen also Gruppen mit symmetrischen Multiplikationstabellen.

Alle zyklischen Gruppen sind abelsch, aber eine abelsche Gruppe ist nicht unbedingt zyklisch. Alle Untergruppen einer abelschen Gruppe sind normal. In einer abelschen Gruppe befindet sich jedes Element in einer eigenen Konjugationsklasse, und die Zeichentabelle enthält Potenzen eines einzelnen Elements, das als Gruppengenerator bekannt ist.

In der Wolfram Language stellt die Funktion AbelianGroup das direkte Produkt der zyklischen Gruppen der Grade , , ….

Es ist keine allgemeine Formel bekannt, um die Anzahl der nicht-isomorphen endlichen Gruppen einer bestimmten Gruppenordnung anzugeben. Die Anzahl der nichtisomorphen abelschen endlichen Gruppen einer gegebenen Gruppenordnung ist jedoch gegeben, wenn man schreibt als

(1)

wobei die verschiedene Primfaktoren sind, dann

(2)

wobei die Partitionsfunktion ist, die in der Wolfram Language als FiniteAbelianGroupCount implementiert ist. Die Werte von für , 2, … sind 1, 1, 1, 1, 2, 1, 1, 1, 3, 2, … (OEIS A000688).

Die kleinsten Ordnungen, für die , 2, 3, … nichtisomorphe abelsche Gruppen existieren, sind 1, 4, 8, 36, 16, 72, 32, 900, 216, 144, 64, 1800, 0, 288, 128, … (OEIS A046056), wobei 0 eine unmögliche Zahl (d. h. kein Produkt von Teilungszahlen) von nicht-isomorphen abelschen Gruppen bezeichnet. Die „fehlenden“ Werte sind 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41, 43, 46, … (OEIS A046064). Die inkrementell größten Zahlen der abelschen Gruppen in Abhängigkeit von der Ordnung sind 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, … (OEIS A046054), die für die Ordnungen 1, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, … (OEIS A046055).

Das Kronecker-Zerlegungs-Theorem besagt, dass jede endliche abelsche Gruppe als direktes Produkt zyklischer Gruppen der Primzahl-Gruppenordnung geschrieben werden kann. Ist die Gruppenordnung einer endlichen Gruppe eine Primzahl , so gibt es eine einzige abelsche Gruppe der Ordnung (bezeichnet als ) und keine nicht-abelschen Gruppen. Ist die Gruppenordnung eine Primzahl zum Quadrat , dann gibt es zwei abelsche Gruppen (bezeichnet als und . Ist die Ordnung der Gruppe eine Primzahl kubisch , dann gibt es drei abelsche Gruppen (, und ) und insgesamt fünf Gruppen. Wenn die Ordnung ein Produkt der beiden Primzahlen und ist, dann gibt es genau eine abelsche Gruppe der Gruppenordnung (bezeichnet als ).

Ein weiteres interessantes Ergebnis ist, dass wenn die Anzahl der nichtisomorphen abelschen Gruppen der Gruppenordnung bezeichnet, dann

(3)

wobei die Riemannsche Zeta-Funktion ist.

Die Zahlen der abelschen Gruppen der Ordnung sind gegeben durch 1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15, 17, 18, 19, 20, 25, … (OEIS A063966) für , 2, …. Srinivasan (1973) hat auch gezeigt, dass

(4)

wobei

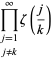			(5)
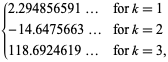			(6)

(OEIS A021002, A084892 und A084893) und ist wiederum die Riemannsche Zeta-Funktion. Man beachte, dass Richert (1952) fälschlicherweise angegeben hat. Die Summen können auch in den expliziten Formen geschrieben werden