Berechnung des durchschnittlichen Jahresschadens
Angenommen, Sie möchten den AAL für ein geografisch verstreutes Portfolio von Immobilien anhand eines 10-Jahres-Hurrikan-Katalogs berechnen (beachten Sie, dass es sich hierbei um ein erfundenes Beispiel handelt, das nur der Veranschaulichung dient; tatsächliche Kataloge enthalten in der Regel 10.000, 50.000 oder sogar 100.000 Jahre simulierter Aktivität). In jedem simulierten Jahr kann es null, einen oder mehrere Hurrikane geben, die das Portfolio beeinflussen. Die Ausführung des Modells mit diesem Portfolio in der AIR-Software führt zu den in Tabelle 1 dargestellten Schäden.
| Hurrikan | |
|---|---|
| Simulationsjahr | Schaden (in Millionen USD) |
| 1 | 25 |
| 2 | 0 |
| 3 | 17 |
| 4 | 34 |
| 5 | 99 |
| 6 | 67 |
| 7 | 0 |
| 8 | 31 |
| 9 | 55 |
| 10 | 29 |
Diese Verluste werden dann in eine Rangfolge gebracht, um eine Kurve der Überschreitungswahrscheinlichkeit zu erstellen, und auch gemittelt, um den Gesamt-AAL zu berechnen, wie in Abbildung 1 dargestellt. In diesem Beispiel beträgt der AAL 36 Mio. USD. Es fällt auf, dass sieben Jahre niedrigere Verluste als die AAL verursachen und drei Jahre höhere Verluste. In zwei Jahren war das Portfolio von keinem Wirbelsturm betroffen, und die Verluste waren gleich Null.
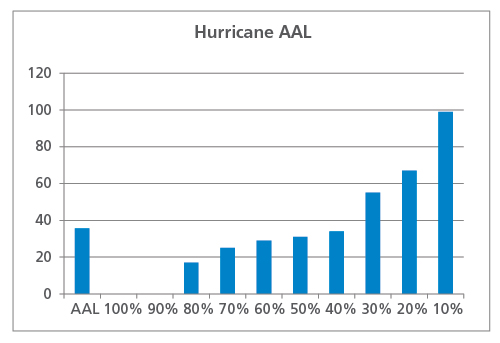
Was AAL nicht verrät
Angenommen, dass dasselbe hypothetische Portfolio von Immobilien in der Nähe einer Erdbebenverwerfung liegt, die voraussichtlich einmal alle fünf Jahre ausbricht. Die Anwendung eines 10-Jahres-Erdbebenkatalogs auf das Portfolio könnte zu den in Tabelle 2 aufgeführten Verlusten führen.
| Erdbeben | |
|---|---|
| Simulationsjahr | Verlust (Mio. USD) |
| 1 | 0 |
| 2 | 0 |
| 3 | 250 |
| 4 | 0 |
| 5 | 0 |
| 6 | 0 |
| 7 | 0 |
| 8 | 0 |
| 9 | 150 |
| 10 | 0 |
Die EP-Kurve und AAL können wie zuvor berechnet werden, wie in Abbildung 2 dargestellt. Der AAL für Erdbeben ist mit 40 Mio. USD dem für Hurrikane sehr ähnlich, aber es ist sofort ersichtlich, dass das Risikoprofil dieser beiden Gefahren sehr unterschiedlich ist.
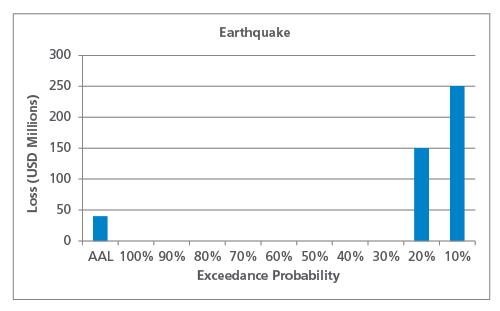
Wie dieses vereinfachte Beispiel zeigt, trägt bei Gefahren, die durch seltene Schadensereignisse gekennzeichnet sind (wie Erdbeben), das Ende der Verteilung mit geringer Häufigkeit und hohen Auswirkungen mehr zum AAL bei als Gefahren, die eine höhere Häufigkeit von weniger schädlichen Ereignissen aufweisen. Dies ist wichtig zu beachten, wenn man die historische AAL (die auf der Grundlage einer begrenzten Anzahl von Jahren berechnet wurde) mit der modellierten AAL vergleicht. Bei Gefahren, deren AAL durch den Schwanz der Verteilung bestimmt wird, wird die historische AAL wahrscheinlich viel niedriger sein als die modellierte, wenn innerhalb der Zeitspanne der aufgezeichneten Daten kein großes Ereignis eingetreten ist.
Aggregat- und Ereignis-AAL
Wie bereits erwähnt, kann die AAL auf der Basis von Aggregaten oder Ereignissen bestimmt werden. Wie in der Natur kann es in jedem Jahr null, ein oder mehrere Schadenereignisse geben, und bei der aggregierten AAL werden alle schadenverursachenden Ereignisse in jedem simulierten Jahr berücksichtigt. Die Verluste aus allen Ereignissen werden addiert und dann durch die Anzahl der Jahre im Katalog geteilt, wie in den Beispielen im vorigen Abschnitt gezeigt.
Ereignis-AAL hingegen basiert nur auf dem größten Verlust in jedem simulierten Jahr, d.h. wenn zwei identische Verluste im selben Jahr auftreten, trägt nur einer zur Ereignis-AAL bei. Das folgende Beispiel erläutert die Berechnung konzeptionell. Beachten Sie jedoch, dass die Ereignis-AAL keinen sehr aussagekräftigen Überblick über das Risiko bietet; es wird empfohlen, die Gesamt-AAL zu verwenden.
Tabelle 3 zeigt denselben 10-Jahres-Hurrikan-Katalog, diesmal jedoch aufgeschlüsselt nach Ereignissen. Der größte Verlust aus jedem Jahr ist hervorgehoben.
Tabelle 3. Hypothetischer 10-Jahres-Katalog der Hurrikane, aufgeschlüsselt nach Ereignis
| Hurrikan | ||
|---|---|---|
| Simulationsjahr | Ereignisnummer | Schaden (Millionen USD) |
| 1 | 1 | 25 |
| 2 | 0 | |
| 3 | 2 | 13 |
| 3 | 4 | |
| 4 | 4 | 27 |
| 5 | 7 | |
| 5 | 6 | 16 |
| 7 | 2 | |
| 8 | 49 | |
| 9 | 32 | |
| 6 | 10 | 43 |
| 11 | 11 | |
| 12 | 13 | |
| 7 | 0 | |
| 8 | 13 | 31 |
| 9 | 14 | 55 |
| 10 | 15 | 7 |
| 16 | 22 | |
Nur unter Berücksichtigung des größten Verlustes aus jedem Jahr, Die Kurve des Auftretens EP und des Auftretens AAL ist in Abbildung 3 dargestellt.
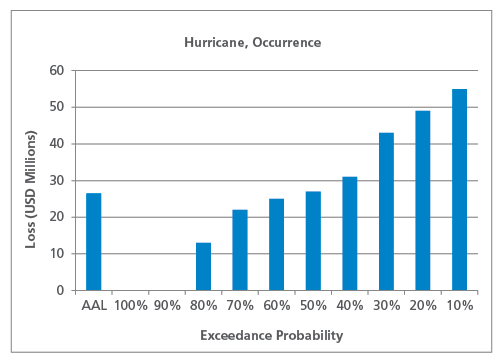
Wie erwartet, ist die Ereignis-AAL (mit 26,5 Mio. USD) niedriger als die Gesamt-AAL. Auch hier wirkt sich die Art der Gefahr auf die Form der Ereignis-EP-Kurve und das Verhältnis zwischen Ereignis-AAL und Gesamt-AAL aus. Bei Gefahren mit geringerer Häufigkeit, wie z. B. Erdbeben, ist es weniger wahrscheinlich, dass mehrere Schadensereignisse im selben Jahr auftreten, so dass die Eintrittswahrscheinlichkeit AAL näher an der Gesamt-AAL liegt als bei Gefahren mit höherer Häufigkeit, wie z. B. schweren Gewitterstürmen.
Abschließende Überlegungen
Auch wenn die Beispiele in diesem Artikel zu Anschauungszwecken stark vereinfacht wurden, so ist doch grundsätzlich festzustellen, dass die AAL zwar nur eine einzige Zahl ist und immer auf dieselbe Weise berechnet wird, dass aber die ihr zugrunde liegende Verteilung je nach Gefahr, Region und anderen Gefahren- und Gefährdungsmerkmalen sehr unterschiedlich aussehen kann. Wir werden das Konzept der EP-Kurvenformen und ihre Auswirkungen auf die AAL in einem kommenden Artikel genauer untersuchen und auch auf einige häufig gestellte Fragen und Missverständnisse über die AAL eingehen.