Schauen Sie sich die jüngsten Artikel an

Abstract

Licht bewegt sich mit der Geschwindigkeit c durch ein Vakuum, unabhängig von der Bewegung der Lichtquelle oder der des Bezugssystems eines Beobachters. Folglich benötigt das Licht eine gewisse Zeit, um von einer Lichtquelle zu einem Beobachter im Raum zu gelangen, so dass die Emission von Licht und die Beobachtung des emittierten Lichts nicht gleichzeitig erfolgen. Auf der Grundlage dieser Überlegungen wird eine Methode zur Messung der absoluten Geschwindigkeit eines Beobachters vorgeschlagen, die zur Bestimmung des Bewegungszustandes eines Raumfahrzeugs in einer geschlossenen Kabine verwendet werden könnte. In dieser Studie wird auch eine neue Erklärung der Lorentz-Transformation eingeführt.

Schlüsselwörter

Koordinatensystem, Bezugssystem, Bewegung, absolute Geschwindigkeit, Relativität, Lorentz-Transformation, Zeit, Raum, Beobachter, Lichtquelle
In der folgenden Analyse wird ein praktischer Ansatz zur Messung der absoluten Geschwindigkeit eines Beobachters vorgestellt, der zur Bestimmung des Bewegungszustands eines Raumfahrzeugs in einer geschlossenen Kabine verwendet werden könnte. Der Begriff der absoluten Geschwindigkeit bezieht sich im Allgemeinen auf eine einheitliche Geschwindigkeit der verschiedenen Objekte eines physikalischen Systems relativ zu einem postulierten unbeweglichen Raum, der unabhängig von den darin enthaltenen physikalischen Objekten existiert (d. h. ein absoluter Raum). Wir stellen hier einen auf der starren Kinematik basierenden Ansatz vor, um zu zeigen, dass die absolute Geschwindigkeit eines Beobachters aus der Tatsache abgeleitet werden kann, dass sich Licht mit der Geschwindigkeit c durch ein Vakuum bewegt, unabhängig von der Bewegung der Lichtquelle oder des Bezugssystems des Beobachters. Folglich benötigt das Licht eine gewisse Zeit, um von einer Lichtquelle zu einem Beobachter im Raum zu gelangen, so dass die Emission von Licht und die Beobachtung des emittierten Lichts nicht gleichzeitig erfolgen.
In der vorgeschlagenen Analyse geben wir zunächst die folgenden Konventionen für die betrachteten Koordinatensysteme an. Wir gehen von einem kartesischen Koordinatensystem aus, das aus drei paarweise aufeinander senkrecht stehenden Achsen besteht, die vom Punkt (0,0,0) ausgehen, wobei jeder Punkt P im Raum durch seine Koordinaten entlang der x-, y- und z-Achse definiert werden kann, die durch ein geordnetes Paar reeller Zahlen (x,y,z) dargestellt werden. Ein Trägheitsreferenzsystem S wird durch ein rechtwinkliges Raumkoordinatensystem (x,y,z) dargestellt, dessen Ursprung O ist. Eine Reihe von Standarduhren (bezeichnet als S-Uhren) befinden sich an stationären Punkten in S. Die S-Uhren sind gegenseitig kalibriert (d. h. sie liefern gleichwertige Ablesungen zum gleichen Zeitpunkt), basierend auf der Übertragung und dem Empfang eines Lichtsignals. Konkret wird zum Zeitpunkt tA ein Lichtstrahl von der Uhr A zur Uhr B projiziert, der dann zum Zeitpunkt tB von der Uhr B zurück zur Uhr A reflektiert wird und zum Zeitpunkt tA‘ bei der Uhr A eintrifft. Wenn , sind die beiden Uhren kalibriert. Für jedes Ereignis, das sich an den Koordinaten x,y,z befindet, ist seine Zeitkoordinate t durch den Stand der ereignisbezogenen Uhr S gegeben. In ähnlicher Weise wird ein weiteres Trägheitsreferenzsystem S‘ auf der Grundlage eines zweiten raumbezogenen rechtwinkligen Koordinatensystems (x‘,y‘,z‘), dessen Ursprung O‘ ist, eingerichtet, und eine weitere Reihe von gegenseitig geeichten Standarduhren (S‘-Uhren) befinden sich an stationären Punkten im Referenzsystem S‘. Für jedes Ereignis, das sich an den Koordinaten x‘,y‘,z‘ befindet, ist seine Zeitkoordinate t‘ durch die Ablesung der ereignisbezogenen S‘-Uhr gegeben.
Da die jeweiligen Ursprünge der Raum- und Zeitkoordinaten sowie die Richtungen der Koordinatenachsen weitgehend willkürlich gewählt werden können, beruhen die hier verwendeten Beziehungen zwischen S und S‘ auf den folgenden Konventionen, die der Einfachheit halber angewendet wurden.
(1) Zu einem bestimmten Zeitpunkt liegen die Ursprünge und Koordinatenachsen der beiden Systeme übereinander, und die Uhren, die sich bei O bzw. O‘ befinden, werden auf Null gestellt, d.h., .
(2) Die Achsen x und x‘ fallen in der Richtung der Relativbewegung von S und S‘ zusammen; x und x‘ sind also jederzeit deckungsgleich, während y und y‘ sowie z und z‘ parallel sind.
(3) S‘ bewegt sich entlang der +x-Richtung von S.
Die vorgeschlagene Analyse basiert auf dem fundamentalen Prinzip, dass sich Licht im Vakuum mit konstanter Geschwindigkeit c bewegt, unabhängig von der Bewegung des Beobachters oder der Lichtquelle. Daher definieren wir hier die absolute Geschwindigkeit U des Beobachters, die als linear und gleichförmig angenommen wird, als , wobei f(φ) eine Funktion der geometrischen Beziehung zwischen der Richtung eines Lichtsignals und der Richtung von U darstellt, die hier als φ bezeichnet wird.
Zwei neue Erklärungen der Relativität von Zeit und Länge werden in der vorgeschlagenen Analyse geliefert, die sich von Einsteins Erklärungen unterscheiden (siehe „Zur Elektrodynamik bewegter Körper“). Diese Erklärungen werden in den folgenden Abschnitten vorgestellt.

Die Relativität der Zeit

Aufgrund der endlichen Lichtgeschwindigkeit benötigt das Licht eine gewisse Zeit, um von einer Lichtquelle zu einem Beobachter im Raum zu gelangen. Daraus lässt sich ableiten, dass die Aussendung von Licht und die Beobachtung von Licht nicht gleichzeitig erfolgen können. Ausgehend von der Konstanz der Lichtgeschwindigkeit und den in Abbildung 1 dargestellten Bedingungen definieren wir die folgenden Faktoren. Die Positionen einer Lichtquelle und eines Beobachters zum Zeitpunkt , zu dem die Lichtquelle Licht aussendet (bezeichnet als Ereignis R), werden mit A bzw. H0 angegeben. Während des Zeitraums der Lichtausbreitung von bis legt der Beobachter eine Strecke U∙T von der Position H0 nach H zurück, woraufhin der Beobachter das ausgesendete Licht empfängt. Dementsprechend definieren wir als die Entfernung l zwischen der Position des Beobachters beim Empfang des Lichtsignals bei und der Position der Lichtquelle beim Aussenden des Lichts bei . Aufgrund der Konstanz der Lichtgeschwindigkeit ist . Die Entfernung ist gleich U∙T. Schließlich definieren wir als den Abstand l0 zwischen der Position des Beobachters bei und der Position der Lichtquelle bei . Hier führen wir eine Betrachtung der Position des Beobachters bei ein, von der bisher angenommen wurde, dass sie keine physikalische Bedeutung hat. Wenn die Bewegungszustände des Beobachters und der Lichtquelle äquivalent sind, ist l0 gegeben, so dass U über die in ,Abbildung 1 dargestellten Dreiecksbeziehungen berechnet werden kann.
In der vorliegenden Arbeit wird die Zeit eines Ereignisses nach folgender Methode gemessen. Sowohl der Beobachter als auch eine Uhr befinden sich im Ursprung. Wenn das Lichtsignal, das das Eintreten eines Ereignisses repräsentiert, den Beobachter erreicht, stimmt die Ankunftszeit des Lichts mit der von der Uhr angezeigten Zeit überein. Der Vorteil dieser Korrespondenz besteht darin, dass sie immer mit der Position des Beobachters, der die Uhr verwendet, zusammenhängt. Wie in Abbildung 1 zu sehen ist, kann der räumliche Punkt O3 auf der Grundlage der Position der Lichtquelle definiert werden, wenn diese Licht bei aussendet, und der räumliche Punkt O2 kann auf der Grundlage der Position des Beobachters definiert werden, wenn dieser Licht bei empfängt. Es ist jedoch nicht offensichtlich, wie der räumliche Punkt O1 definiert werden kann, an dem sich der Beobachter befindet, wenn die Lichtquelle Licht bei aussendet. Um dieses Problem zu lösen, werden die Begriffe der absoluten Ruhe (d.h. ) und der absoluten Bewegung (d.h. ) eingeführt. Wir ersetzen den einzelnen bewegten Beobachter in H0 und H durch zwei Beobachter H1 und H2, die in den Raumpunkten O1 bzw. O2 ruhen, während die Lichtquelle A im Raumpunkt O3 ruht. Jeder der Beobachter und die Lichtquelle verwenden geeichte Normaluhren, und A sendet ein Lichtsignal zum Zeitpunkt aus, das als Ereignis R0 bezeichnet wird. Wenn der Beobachter H1 das Lichtsignal empfängt, das sich mit der Geschwindigkeit c fortbewegt, ist der Uhrenstand T0, und wenn H2 das Lichtsignal empfängt, ist der Uhrenstand T. Die Entfernungen und können also auf der Grundlage der jeweiligen Laufzeiten des Lichtsignals wie folgt definiert werden:
, (1)
und
. (2)
Nach den in Abbildung 1 dargestellten Dreiecksbeziehungen ist die Transformation des Ereignisses R0 zwischen den Beobachtern H1 und H2 wie folgt gegeben:
(3)
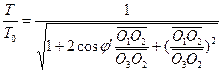(4)
Hier ist der Winkel zwischen der Linie O3O1 und der x-Achse, und der Winkel zwischen der Linie O3O2 und der x-Achse.
Wir kehren nun zu der Bedingung eines einzelnen bewegten Beobachters zurück und nehmen an, dass im System S sowohl der Beobachter H als auch die Lichtquelle A eine geeichte Normaluhr verwenden. Zum Zeitpunkt des Ereignisses R befindet sich die Lichtquelle A im Raumpunkt O3 und der Beobachter H in O1. Der Zeitpunkt, zu dem das Lichtsignal den räumlichen Punkt O1 erreicht, entspricht einem S-Uhrenstand von T0. Wenn der Beobachter H das Lichtsignal empfängt, ist der Stand T, und H befindet sich in O2.
Natürlich kann H das Ereignis R im Punkt O1 nicht beobachten. Um dieses Problem zu lösen, wird ein weiterer Beobachter H- im System S am Punkt O1 platziert, der entspricht, wobei die Position von H- zur Definition des räumlichen Punktes O1 verwendet wird. Dann kann die Transformation des Ereignisses R zwischen den Beobachtern H- und H durch Gleichung (3) wie folgt erhalten werden.
(5)
Die Gleichungen (3) und (4) können also wie folgt umgeschrieben werden.
(6)
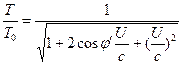(7)
Es ist auch zu beachten, dass sich die Gleichungen (6) und (7) für wie folgt vereinfachen.
(8)
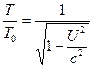(9)
Auf der Grundlage der obigen Analyse kann daher eine einfache Methode zur Bestimmung von U aus Gleichung (6) erhalten werden, vorausgesetzt, dass (φ) bekannt ist.
Der Einfachheit halber wird als Bezugsrahmen eine Lichtquelle gewählt, deren Bewegungszustand dem der Beobachter entspricht. Ein Beobachter wird in die Mitte eines geraden, starren Balkens gesetzt, der sich gleichmäßig linear bewegt, und Lichtsignale von verschiedenen Positionen auf dem Balken erreichen den Beobachter zu verschiedenen Zeiten. Der Beobachter erkennt die Auslenkung des Balkens an der Position des Beobachters mit einem Auslenkungswinkel , der aus Gleichung (8) erhalten werden kann.
Mit dieser Methode kann der Bewegungszustand eines Raumfahrzeugs aus einer geschlossenen Kabine bestimmt werden.

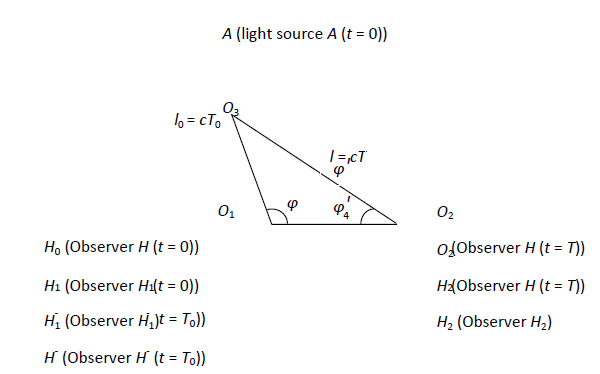
Abbildung 1: Bewegungszustände des Beobachters und der Lichtquelle

Die Relativität der Länge

In der obigen Analyse wurden zwei Längen eingeführt, d.h. und . In diesem Fall betrachten wir die Länge eines Stabes, von dem angenommen wird, dass er ein stationärer starrer Stab der Länge L innerhalb seines Koordinatensystems ist, für den L mit einer stationären Messlatte gemessen wird, und bei dem die Stabachse mit der x-Achse eines Koordinatensystems zusammenfällt, das sich mit einer gleichmäßigen linearen Bewegung entlang der +x-Richtung mit einer absoluten Geschwindigkeit U bewegt. Es wird angenommen, dass L durch die beiden unten definierten Operationen bestimmt wird.
(a) Der Beobachter befindet sich in demselben bewegten Koordinatensystem wie der Stab und die Messlatte, und L wird durch Überlagerung von Stab und Messlatte gemessen.
(b) Mit Hilfe mehrerer Uhren, die sich in stationären Koordinaten befinden und sich synchron bewegen, misst der Beobachter die Positionen der beiden Enden des Stabes in stationären Koordinaten zu einem bestimmten Zeitpunkt t, und der Abstand zwischen den beiden Positionen wird mit der stationären Messlatte gemessen. ist die aus Vorgang (a) berechnete Länge, die hier als Stablänge in den beweglichen Koordinaten bezeichnet wird. ist die aus Operation (b) berechnete Länge, die hier als die Länge eines beweglichen Stabes in der stationären Koordinate bezeichnet wird. Es ist offensichtlich, dass und unterschiedlich sind.
Wir nehmen an, dass sich der Beobachter H- im System S im gleichen Bewegungszustand befindet wie H. Dann befindet sich H-, wie in Abbildung 1 gezeigt, im Punkt O1, wenn er das Lichtsignal bei empfängt, und gleichzeitig befindet sich der Beobachter H im Punkt O4. Daher ist t=0,04
der Abstand zwischen H- und H bei , und
. (10)
ist die vom Beobachter H im Intervall von T0 bis T zurückgelegte Strecke, so dass
. (11)
ist der Abstand zwischen H- bei und H bei , so dass
. (12)
Als solches kann der folgende Ausdruck hergeleitet werden.
(13)
Nachfolgend betrachten wir die Koordinaten- und Zeittransformationen zwischen zwei bewegten Koordinatensystemen, die sich beide mit einer einheitlichen linearen Geschwindigkeit bewegen, was eine neue Erklärung der Lorentz-Transformation darstellt.
Angenommen, der Beobachter H (im System S), der Beobachter H‘ (im System S‘) und die Lichtquelle A“ (im System S“) verwenden alle einzeln geeichte Normaluhren, und zum Zeitpunkt sendet die Lichtquelle A“ ein Lichtsignal aus, das als Ereignis R“ bezeichnet wird. Zum Zeitpunkt des Ereignisses R“ befindet sich A“ im Punkt O3, und die Beobachter H und H‘ sind deckungsgleich. Wenn der Beobachter H das Lichtsignal empfängt, ist der Stand der Uhr S T, und H befindet sich im Punkt O1. Wenn der Beobachter H‘ das Lichtsignal empfängt, ist der Zeiger der Uhr S‘ gleich T‘, und H‘ befindet sich im Punkt O2. Dann kann die Transformation des Ereignisses R“ zwischen den Beobachtern H‘ und H aus Gleichung (3) berechnet werden, wobei
. (14)
Hier ist u die relative Geschwindigkeit zwischen den Beobachtern H‘ und H, woraus sich die folgenden Transformationen ergeben.
(15)
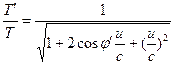(16)
Aus lassen sich die folgenden Beziehungen ableiten:
. (17)
Wenn und , vereinfacht sich Gleichung (16) zu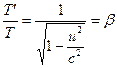
. (18)
Daraus lassen sich die folgenden Transformationsbeziehungen ableiten:
, (19)
, (20)
, (21)
. (22)
Außerdem, wenn ,
, (23)
und
, (24)
, (25)
, (26)
. (27)