Toleranzintervalle
Dieser Abschnitt enthält statistische Angaben zu einseitigen und zweiseitigen Toleranzintervallen.
Normalverteilungsbasierte Intervalle
Einseitiges Intervall
Das einseitige Intervall wird wie folgt berechnet:
Untere Grenze = 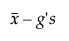
Obere Grenze = 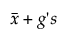
wobei
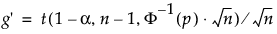
s die Standardabweichung
t das Quantil aus der nichtzentralen t-Verteilung
Φ-1 ist das Standardnormalquantil
Zweiseitiges Intervall
Das zweiseitige Intervall wird wie folgt berechnet:
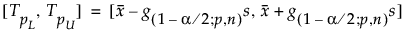
wobei s die Standardabweichung ist und g(1-α/2; p,n) eine Konstante ist.
Um g zu bestimmen, betrachtet man den Anteil der Grundgesamtheit, der durch das Toleranzintervall erfasst wird. Tamhane und Dunlop (2000) geben diesen Anteil wie folgt an:
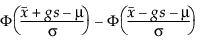
wobei Φ die Standardnormalverteilungsfunktion (cdf) bezeichnet.
Daher löst g die folgende Gleichung:
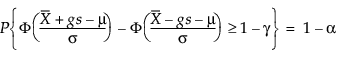
wobei 1 – γ der Anteil aller zukünftigen Beobachtungen ist, der im Toleranzintervall enthalten ist.
Weitere Informationen über Toleranzintervalle auf der Grundlage der Normalverteilung finden Sie in den Tabellen J.1a, J.1b, J.6a und J.6b von Meeker et al. (2017).
Nichtparametrische Intervalle
Einseitige untere Grenze
Die untere einseitige Toleranzgrenze von 100(1 – α)%, die mindestens einen Anteil β der gesampelten Verteilung aus einer Stichprobe des Umfangs n enthält, ist die Ordnungsstatistik x(l). Der Index l wird wie folgt berechnet:
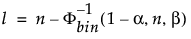
wobei Φ-1bin(1-α, n, β) das (1 – α)-te Quantil der Binomialverteilung mit n Versuchen und Erfolgswahrscheinlichkeit β ist.
Das tatsächliche Konfidenzniveau wird berechnet als Φbin(n-l, n, β), wobei Φbin(x, n, β) die Wahrscheinlichkeit ist, dass eine binomialverteilte Zufallsvariable mit n Versuchen und Erfolgswahrscheinlichkeit β kleiner als oder gleich x ist.
Beachten Sie, dass zur Berechnung eines unteren einseitigen verteilungsfreien Toleranzintervalls der Stichprobenumfang n mindestens so groß sein muss wie 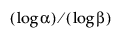 .
.
Einseitige obere Grenze
Die obere 100(1 – α)%ige einseitige Toleranzgrenze, die mindestens einen Anteil β der Stichprobenverteilung aus einer Stichprobe des Umfangs n enthält, ist die Ordnungsstatistik x(u). Der Index u wird wie folgt berechnet:
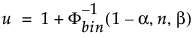
wobei Φ-1bin(1-α, n, β) das (1 – α)-te Quantil der Binomialverteilung mit n Versuchen und Erfolgswahrscheinlichkeit β ist.
Das tatsächliche Konfidenzniveau wird berechnet als Φbin(u-1, n, β), wobei Φbin(x, n, β) die Wahrscheinlichkeit ist, dass eine binomialverteilte Zufallsvariable mit n Versuchen und Erfolgswahrscheinlichkeit β kleiner oder gleich x ist.
Beachten Sie, dass zur Berechnung eines oberen einseitigen verteilungsfreien Toleranzintervalls der Stichprobenumfang n mindestens so groß wie 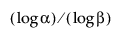 sein muss.
sein muss.
Zweiseitiges Intervall
Das zweiseitige Toleranzintervall von 100(1 – α)%, das mindestens einen Anteil β der gesampelten Verteilung aus einer Stichprobe mit dem Umfang n enthält, wird wie folgt berechnet:
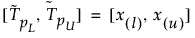
wobei x(i) die Statistik der i-ten Ordnung ist und l und u wie folgt berechnet werden:
Lassen Sie ν = n – Φ-1bin(1-α, n, β), wobei Φ-1bin(1-α, n, β) das (1 – α)-te Quantil der Binomialverteilung mit n Versuchen und Erfolgswahrscheinlichkeit β ist. Wenn ν kleiner als 2 ist, kann kein zweiseitiges verteilungsfreies Toleranzintervall berechnet werden. Ist ν größer oder gleich 2, so ist l = floor(ν/2) und u = floor(n + 1 – ν/2).
Das tatsächliche Konfidenzniveau wird berechnet als Φbin(u-l-1, n, β), wobei Φbin(x, n, β) die Wahrscheinlichkeit ist, dass eine binomialverteilte Zufallsvariable mit n Versuchen und einer Erfolgswahrscheinlichkeit β kleiner oder gleich x ist.
Beachten Sie, dass zur Berechnung eines zweiseitigen verteilungsfreien Toleranzintervalls der Stichprobenumfang n mindestens so groß sein muss wie das n in der folgenden Gleichung:

Weitere Informationen zu verteilungsfreien Toleranzintervallen finden Sie in Meeker et al. (2017, Abschnitt 5.3).