La tercera ley postula que la entropía de una sustancia es siempre finita y que se aproxima a una constante a medida que la temperatura se acerca a cero. El valor de esta constante es independiente de los valores de cualquier otra función de estado que caracterice a la sustancia. Para cualquier sustancia, somos libres de asignar un valor arbitrario al valor límite de la temperatura cero. Sin embargo, no podemos asignar entropías de temperatura cero arbitrarias a todas las sustancias. El conjunto de asignaciones que hagamos debe ser coherente con los valores límite de temperatura cero observados experimentalmente de los cambios de entropía de las reacciones entre diferentes sustancias. Para las sustancias perfectamente cristalinas, estas entropías de reacción son todas cero. Podemos satisfacer esta condición asignando un valor arbitrario a la entropía molar a temperatura cero de cada elemento y estipulando que la entropía a temperatura cero de cualquier compuesto es la suma de las entropías a temperatura cero de sus elementos constitutivos. Este cálculo se simplifica enormemente si dejamos que la entropía a temperatura cero de cada elemento sea cero. Este es el contenido esencial de la tercera ley.
La declaración de Lewis y Randall incorpora esta selección del estado de referencia de entropía cero para las entropías, especificándolo como «un estado cristalino» de cada elemento a cero grados. Como resultado, la entropía de cualquier sustancia a cero grados es mayor o igual a cero. Es decir, el enunciado de Lewis y Randall incluye una convención que fija el valor límite de temperatura cero de la entropía de cualquier sustancia. En este sentido, el enunciado de Lewis y Randall hace una elección esencialmente arbitraria que no es una propiedad intrínseca de la naturaleza. Vemos, sin embargo, que es una elección abrumadoramente conveniente.
Hemos discutido enunciados alternativos de la primera y segunda leyes. También son posibles varios enunciados alternativos de la tercera ley. Consideramos los siguientes:
Es imposible alcanzar una temperatura de cero absoluto.
Esta afirmación es más general que la de Lewis y Randall. Si consideramos la aplicación de esta afirmación a las temperaturas alcanzables en los procesos en los que interviene una sola sustancia, podemos demostrar que implica, y es implicada por, la afirmación de Lewis y Randall.
Las propiedades de la capacidad calorífica, \(C_P\), juegan un papel central en estos argumentos. Hemos visto que \(C_P\) es una función de la temperatura. Aunque no es útil hacerlo, podemos aplicar la relación definitoria de \(C_P\) a una sustancia que sufre una transición de fase y encontrar \(C_P=\infty\). Si pensamos en una sustancia cuya capacidad calorífica sea inferior a cero, nos encontramos con una contradicción de nuestras ideas básicas sobre el calor y la temperatura: Si \(q>0\) y \({q}/{\Delta T}<0\), debemos tener \(\Delta T<0\); es decir, el calentamiento de la sustancia hace que su temperatura disminuya. En resumen, la teoría que hemos desarrollado incorpora premisas que requieren \(C_P>0\) para cualquier sistema sobre el que podamos realizar mediciones.
Caractericemos un sistema de sustancia pura por su presión y temperatura y consideremos procesos reversibles de presión constante en los que sólo es posible el trabajo presión-volumen. Entonces \({\left({\partial S}/{partial T}\right)}_P={C_P}/{T}\) y \(dS={C_PdT}/{T}\). Ahora queremos demostrar: la estipulación de Lewis y Randall de que la entropía es siempre finita requiere que la capacidad calorífica llegue a cero cuando la temperatura llega a cero. (Como vamos a demostrar que la tercera ley prohíbe las mediciones en el cero absoluto, esta conclusión es coherente con nuestra conclusión del párrafo anterior). Que la capacidad calorífica llega a cero cuando la temperatura llega a cero es evidente a partir de \(S={C_PdT}/{T}.\ Si \(C_P\) no llega a cero cuando la temperatura llega a cero, \(dS\) se hace arbitrariamente grande cuando la temperatura llega a cero, lo que contradice la afirmación de Lewis y Randall.
Para desarrollar este resultado de forma más explícita, dejamos que las capacidades caloríficas a las temperaturas \(T\) y cero sean \(C_P\left(T\right)\) y \(C_P\left(0\right)\), respectivamente. Dado que \(C_P\left(T\right)>0\ para cualquier \(T\ >\ 0\), tenemos \(S\left(T\right)-S\left(T^*\right)>0\) para cualquier \(T>T^*>0\). Como la entropía es siempre finita, \(\infty >S\left(T\right)-S\left(T^*\right)>0\), por lo que
\ }>0\]
y
Para temperaturas en la vecindad de cero, podemos expandir la capacidad calorífica, con una precisión arbitraria, como un polinomio en serie de Taylor en \(T\):
\
Las desigualdades se convierten en
\
La condición de la izquierda requiere \(C_P\left(0\right)=0\).
Podríamos ver la tercera ley como una afirmación sobre las capacidades caloríficas de las sustancias puras. Inferimos no sólo que \(C_P>0\) para todo \(T>0\), sino también que
\
De forma más general, podemos inferir las afirmaciones correspondientes para sistemas reversibles cerrados que no son sustancias puras: \(izquierda (H parcial/t parcial derecha)) para todo (T>0), y (izquierda (H parcial/t parcial derecha)) para todo (T=0). (Sin embargo, las entropías a temperatura cero de tales sistemas no son cero.) En la discusión que sigue, describimos el sistema como una sustancia pura. Podemos hacer esencialmente los mismos argumentos para cualquier sistema; sólo tenemos que reemplazar \(C_P\) por \({\left({\tial H}/{\tial T}\right)}_P\). El enunciado de Lewis y Randall afirma que la entropía llega a una constante en el cero absoluto, independientemente de los valores de cualquier otra función termodinámica. Se deduce que la entropía a cero grados es independiente del valor de la presión. Para dos presiones cualesquiera, \(P_1\) y \(P_2\), tenemos \(S\left(P_2,0\right)-S\left(P_1,0\right)=0\). Dejando que \({P=P}_1\) y \(P_2=P+\Delta P\) y, tenemos
\
para cualquier \(\Delta P\). Por lo tanto, tenemos
\
En el capítulo 10, encontramos \({\left({\tial S}/{partial }P\right)}_T=-{left({\tial V}/{partial T}\right)}_P\), por lo que tanto la entropía como el volumen se aproximan a sus valores de temperatura cero asintóticamente.
Cuando decimos que el cero absoluto es inalcanzable, queremos decir que ningún sistema puede sufrir ningún cambio en el que su temperatura final sea cero. Para ver por qué el cero absoluto debe ser inalcanzable, consideremos los procesos que pueden disminuir la temperatura de un sistema. En general, tenemos depósitos de calor disponibles a varias temperaturas. Podemos seleccionar el depósito disponible cuya temperatura sea la más baja, y llevar el sistema a esta temperatura por simple contacto térmico. Esto es trivial; evidentemente, el reto es disminuir la temperatura aún más. Para ello, debemos realizar algún otro cambio. Cualquiera que sea este cambio, no puede ser ayudado por un intercambio de calor con el entorno. Una vez que hayamos llevado el sistema a la temperatura de la parte más fría del entorno, cualquier otro intercambio de calor con el entorno sólo puede ser contraproducente. Llegamos a la conclusión de que cualquier proceso adecuado a nuestro propósito debe ser adiabático. Como un proceso adiabático no intercambia calor con el entorno, \(\Delta \hat{S}=0\).
El proceso debe ser también un proceso posible, de modo que \(\Delta S+\Delta \hat{S}ge 0\), y como es adiabático, \(\Delta S\ge 0\). Consideremos un proceso reversible y otro irreversible en los que el mismo sistema({}^{2}\a) pasa del estado especificado por \(P_1\a) y \(T_1\a) a un segundo estado en el que la presión es \(P_2\a). Las temperaturas finales y los cambios de entropía de estos procesos son diferentes. Para el proceso reversible, \(\Delta S=0\); designamos la temperatura final como \(T_2\). Para el proceso irreversible, \(\Delta S>0\); designamos la temperatura final como \(T^*_2\). Resulta que el cambio de temperatura es menor para el proceso irreversible que para el proceso reversible; es decir, \(T_2-T_1<t^*_2-t_1\)>. Equivalentemente, el proceso reversible alcanza una temperatura más baja: \({T_2<t}^*_2\)>. A partir de
\
podemos calcular los cambios de entropía para estos procesos. Para el proceso reversible, calculamos \
Para ello, primero calculamos
\
para la transformación reversible isotérmica del estado \(P_1\), \(T_1\) al estado especificado por \(P_2\) y \(T_1\). Para este paso, \(dT\) es cero, y por lo tanto
\
Calculamos a continuación
\
para la transformación reversible isobárica del estado \(P_2\), \(T_1) al estado \(P_2\), \(T_2\). Para esta transformación, \(dP\) es cero, y
\
Entonces,
\
Porque \(\Delta S^{rev}=0\), el proceso reversible es único; es decir, dados \(P_1\), \(T_1\), y \(P_2\), se determina la temperatura final del sistema. Encontramos \(T_2\) a partir de
\
Para entender el cambio de entropía para el proceso irreversible, observamos primero que hay un número infinito de tales procesos. No hay nada único en la temperatura final. Dados \(P_1\), \(T_1\), y \(P_2\), la temperatura final, \(T^*_2\), puede tener cualquier valor consistente con las propiedades de la sustancia. Para especificar un proceso irreversible concreto, debemos especificar las cuatro cantidades \(P_1\), \(T_1\), \(P_2\) y \(T^*_2\). Una vez hecho esto, sin embargo, podemos calcular el cambio de entropía para el proceso irreversible,
\Ncalculando los cambios de entropía a medida que llevamos reversiblemente el sistema a lo largo del camino isotérmico de dos pasos desde \N(P_1\) \(T_1\) a \(P_2\), \(T_1\) y luego a lo largo de la trayectoria isobárica de \(P_2\), \(T_1\) a \(P_2\), \(T^*_2\). El cálculo de \(\Delta S^{irrev}\) para esta trayectoria reversible de \(P_1\), \(T_1\) a \(P_2\), \(T^*_2\) emplea la misma lógica que el cálculo, en el párrafo anterior, de \(\Delta S\) para la trayectoria reversible de \(P_1\), \(T_1\) a \(P_2\), \(T_2\). La diferencia es que \(T^*_2\) sustituye a \(T_2\) como límite superior en la integral de temperatura. La integral de presión es la misma. Tenemos
\️
De \(\Delta S^{irrev}>\️), tenemos
\️
Como las integrales son iguales y positivas, se deduce que \(T^*_2>T_2\️), como se ha afirmado anteriormente.
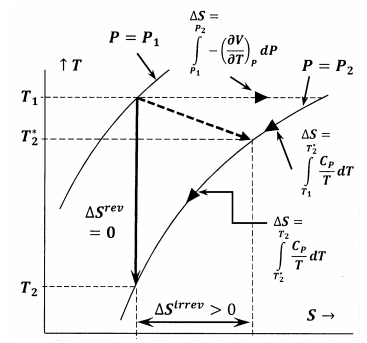
La figura 6 muestra las relaciones entre las distintas magnitudes tratadas en este argumento. En primer lugar, la Figura 6 muestra un gráfico de dos de las isobaras del sistema en el espacio temperatura-entropía. Es decir, la línea etiquetada \(P=P_1\) representa el conjunto de puntos de temperatura-entropía en los que el sistema equilibrado tiene una presión \(P_1\); la línea etiquetada \(P=P_2\), representa las posiciones de equilibrio a la presión \(P_2\). Otras líneas de este esquema representan trayectorias a lo largo de las cuales el sistema puede sufrir cambios reversibles a entropía o temperatura constantes. La línea punteada representa el proceso irreversible en el que el sistema pasa del estado especificado por \(P_1\), \(T_1\) al estado especificado por \(P_2\), \(T^*_2\). Esta línea está punteada para representar el hecho de que la temperatura del sistema puede no estar bien definida durante el proceso irreversible.
El enfriamiento efectivo puede lograrse utilizando cambios de presión si el sistema es un gas. Sin embargo, en el caso de los líquidos y los sólidos, \({\left({\partial V}/{partial T}\right)}_P\) es pequeño; en consecuencia, el cambio de temperatura para un cambio de presión reversible también es pequeño. A temperaturas cercanas al cero absoluto, casi todas las sustancias son sólidas; para lograr un enfriamiento efectivo debemos cambiar una variable termodinámica para la cual el coeficiente de temperatura de un sólido sea lo más grande posible. Para considerar el problema general de la disminución de la temperatura de un sistema variando algo distinto de la presión, debemos considerar un sistema en el que sea posible alguna forma de trabajo no relacionado con la presión y el volumen. Tal sistema está sujeto a una fuerza adicional, y su energía cambia a medida que esta fuerza cambia.
Desmagnetización adiabática
El método práctico por el cual se logran temperaturas extremadamente bajas se llama desmagnetización adiabática. Este método aprovecha las propiedades de los sólidos paramagnéticos. En estos sólidos, los electrones no apareados localizados en átomos individuales dan lugar a un momento magnético. La mecánica cuántica lleva a importantes conclusiones sobre la interacción entre estos momentos magnéticos y un campo magnético aplicado: En un campo magnético aplicado, el momento magnético de un átomo individual se cuantifica. En el caso más sencillo, sólo puede alinearse en dos direcciones: debe ser paralelo o antiparalelo al campo magnético aplicado. Cuando el momento magnético de un átomo es paralelo al campo magnético, la energía del sistema es menor que cuando la alineación es antiparalela. El campo magnético aplicado ejerce una fuerza sobre los momentos magnéticos asociados a los átomos individuales. La energía del sistema depende de la magnitud del campo magnético aplicado.
En lugar de centrarnos en el caso particular de la desmagnetización adiabática, consideremos los cambios de energía y entropía asociados a los cambios en un potencial generalizado, \({\mathit{\Phi}}_{\theta }\), y su desplazamiento generalizado, \(\theta\). (Para la desmagnetización adiabática, \(\theta\) sería el campo magnético aplicado). Se requieren tres variables para describir los cambios reversibles en este sistema. Podemos expresar la energía y la entropía como funciones de la temperatura, la presión y \(\theta\):
(E=E\left(T,P,\theta\right)\) y \(S=S\left(T,P,\theta\right)\). El diferencial total de la entropía incluye un término que especifica la dependencia de la entropía de \(\theta\). Tenemos
donde escribimos \(C\left(T,P,\theta \right)\) para enfatizar que nuestros propósitos actuales exigen que midamos la capacidad calorífica a presión constante y \theta\ constante.
Para una presión constante, P, y un desplazamiento constante, \(\theta\), la entropía depende de la temperatura como
\
El postulado de que la entropía sea finita a cualquier temperatura implica que la capacidad calorífica dependiente de la presión y \(\theta\) se hace cero en el cero absoluto. Es decir, en el cero absoluto, la capacidad calorífica se desvanece sean cuales sean los valores de P y de \theta. El argumento es exactamente el mismo que antes. Antes escribimos \(C_P\left(0\right)=0\); para el presente caso generalizado, escribimos \(C\left(0,P,\theta \right)=0\).
De forma similar, del postulado de que la entropía va a una constante en el cero absoluto para todos los valores de las otras variables termodinámicas, se deduce que, para dos presiones cualesquiera \(P_1\) y \(P_2\), y para dos valores cualesquiera del desplazamiento generalizado, \({\theta }_1\) y \({\theta }_2\),
\
y, por tanto, que
\ y \
Queremos considerar un proceso en el que un sistema pasa de la temperatura más baja disponible en el entorno a una temperatura aún más baja. Para minimizar la temperatura final, este proceso debe realizarse adiabáticamente. También debe ser un proceso posible, de modo que \(dS\ge 0\). Para simplificar, supongamos ahora que realizamos este proceso a una presión constante, \(P\), y que el sistema pasa del estado especificado por \(P\), \(T_1\), \({\theta }_1\) al estado especificado por \(P\), \(T_2), \({\theta }_2\) donde \(T_1>T_2\). Las entropías de estos dos estados son
\ y \
El cambio de entropía para este proceso es
\
Ahora, supongamos que la temperatura final es cero; es decir, \(T_2=0\), por lo que
se deduce que \
donde la desigualdad de la derecha se deduce del hecho de que \(C\left(T,P,{\theta }_1\right)>0\). Entonces, se deduce que
\\Ndebe ser así, lo que contradice el enunciado de Lewis y Randall de la tercera ley. La suposición de que el sistema puede alcanzar el cero absoluto conduce a una contradicción del enunciado de Lewis y Randall de la tercera ley. Por lo tanto, si el enunciado de Lewis y Randall es verdadero, el cero absoluto es inalcanzable.
Lo contrario también se aplica; es decir, a partir de la proposición de que el cero absoluto es inalcanzable, podemos demostrar que el enunciado de Lewis y Randall es verdadero. Para ello, reordenamos la ecuación anterior para \(\Delta S\),
\Nsupongamos ahora que la afirmación de Lewis y Randall es falsa, la expresión de la derecha puede ser menor o igual a cero. La integral de la izquierda puede entonces ser cero, en cuyo caso el sistema puede alcanzar el cero absoluto. Si la afirmación de Lewis y Randall es falsa, es cierto que el sistema puede alcanzar el cero absoluto. Por lo tanto: Si el sistema no puede alcanzar el cero absoluto, la afirmación de Lewis y Randall es verdadera.
Las figuras 7 y 8 representan estas ideas utilizando gráficos de contorno en el espacio temperatura-entropía. Cada figura muestra dos curvas de nivel. Una de estas curvas de nivel es un conjunto de valores de temperatura y entropía a lo largo de los cuales la presión es constante a \(P\) y \(\theta\) es constante a \({\theta }_1\). La otra línea de contorno es un conjunto de valores de temperatura y entropía a lo largo de los cuales la presión es constante en \(P\) y \(\theta\) es constante en \({\theta }_2\). La pendiente de una recta de contorno es
Debido a que la capacidad calorífica es siempre positiva, esta pendiente es siempre positiva.
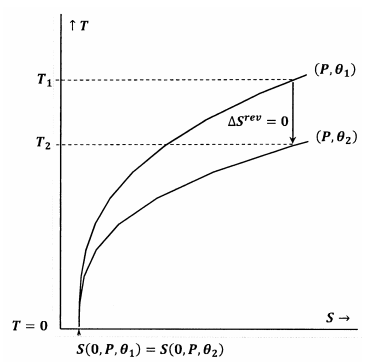
En la figura 7, se satisface el enunciado de Lewis y Randall. Cuando la temperatura llega a cero, las curvas de nivel se encuentran en el mismo valor de la entropía; estas curvas de nivel satisfacen la relación
\
Una trayectoria adiabática (vertical) desde el contorno para \(P\) y \({\theta }_1\) se encuentra con el contorno para \(P\) y \({\theta }_2\) a una temperatura positiva, \(T_2>0\). Como esto es evidentemente cierto para cualquier \(P\) y cualquier \({\theta }_2\), el estado final para cualquier proceso adiabático tendrá \(T_2>0\). Como se satisface el enunciado de Lewis y Randall, el sistema no puede alcanzar el cero absoluto, y viceversa.
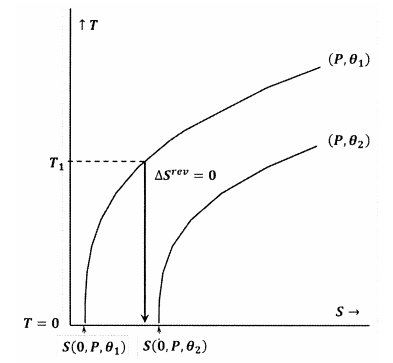
En la figura 8, se viola el enunciado de Lewis y Randall, ya que tenemos \N(S\left(0,P,{\theta }_1\right)\N-.) En este caso, un proceso adiabático iniciado a partir de una temperatura inicial suficientemente baja, \(T_1\), alcanzará el cero absoluto sin intersecar el contorno para la constante \(P\) y \({\theta }_2\). Debido a que la declaración de Lewis y Randal es violada, el sistema puede alcanzar el cero absoluto, y viceversa.