Convoluciones en 1D y 3D explicadas con… ¡MS Excel!

Empezamos con las Convoluciones en 2D en el primer post porque las convoluciones ganaron mucha popularidad después de los éxitos en el campo de la Visión por Computador. Dado que las tareas en este dominio utilizan imágenes como entradas, y las imágenes naturales suelen tener patrones a lo largo de dos dimensiones espaciales (de altura y anchura), es más común ver ejemplos de Convoluciones 2D que Convoluciones 1D y 3D.

Más recientemente, sin embargo, ha habido un gran número de éxitos en la aplicación de convoluciones a las tareas de procesamiento del lenguaje natural también. Dado que las tareas en este ámbito utilizan texto como entrada, y el texto tiene patrones a lo largo de una sola dimensión espacial (es decir, el tiempo), las convoluciones 1D son un gran ajuste. Podemos utilizarlas como alternativas más eficientes a las redes neuronales recurrentes (RNN) tradicionales, como las LSTM y las GRU. A diferencia de las RNN, pueden ejecutarse en paralelo para realizar cálculos realmente rápidos.

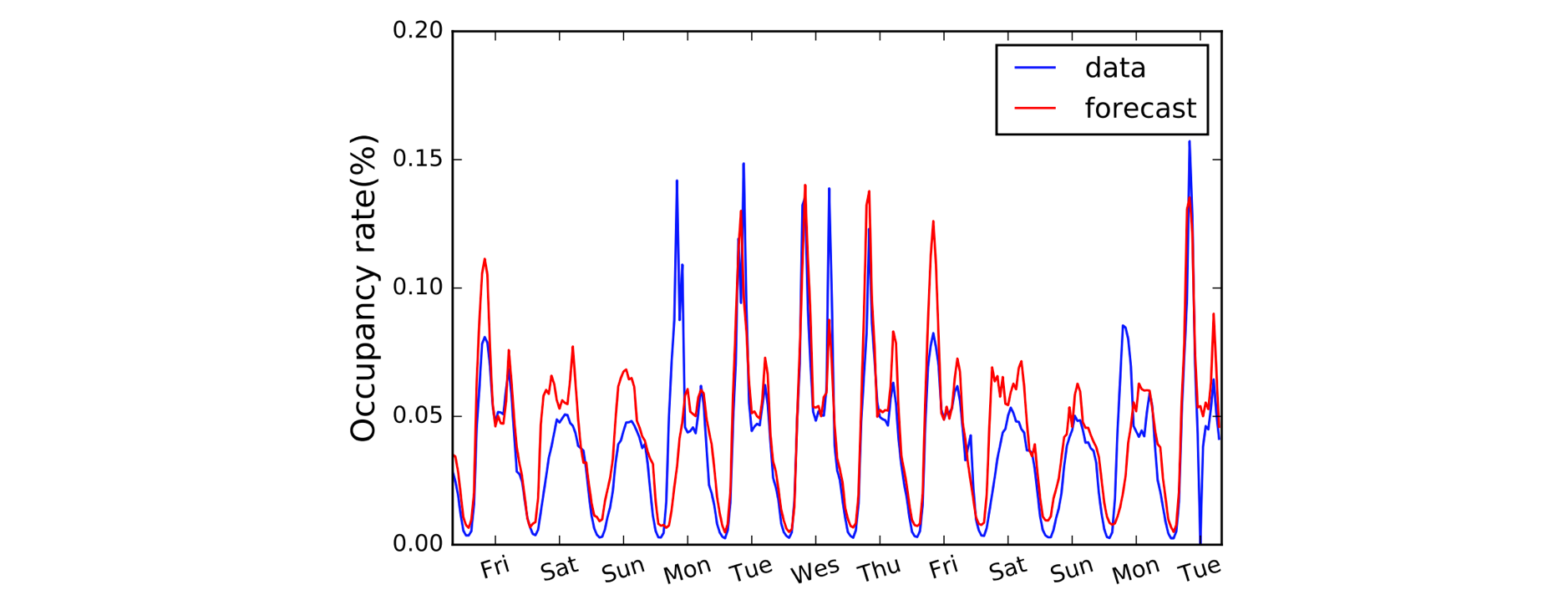
Otro campo que se beneficia de las Convoluciones 1D es la modelización de series temporales. Como antes, tenemos una sola dimensión espacial en nuestros datos de entrada (es decir, el tiempo), y queremos recoger patrones a lo largo de períodos de tiempo. A menudo llamamos a este tipo de datos «secuenciales» porque pueden verse como una secuencia de valores. Y a la dimensión espacial solemos llamarla dimensión «temporal». El uso de convoluciones 1D antes de las RNN es también bastante común: el modelo LSTNet es un ejemplo de ello y sus predicciones para la previsión del tráfico se muestran a continuación.

A, B, C. Es fácil ya que (1,3,3) punto (2,0,1) = 5.

Aclaradas las convenciones de nomenclatura, veamos ahora con más detalle la aritmética. Estamos de suerte porque las Convoluciones 1D son en realidad una versión simplificada de la Convolución 2D!

Trabajando en el cálculo de un único valor de salida, podemos aplicar nuestro núcleo de tamaño 3 a la región de tamaño equivalente en el lado izquierdo de nuestra matriz de entrada. Calculamos el «producto punto» de la región de entrada y el kernel, que para recapitular es simplemente el producto elemento-sabio (es decir, multiplicar los pares de colores) seguido de una suma global para obtener un único valor. Así que en este caso:

(1*2) + (3*0) + (3*1) = 5

Aplicamos la misma operación (con el mismo kernel) a las otras regiones de la matriz de entrada para obtener la matriz de salida completa de (5,6,7,2); es decir, deslizamos el kernel por toda la matriz de entrada. A diferencia de las Convoluciones 2D, donde deslizamos el kernel en dos direcciones, para las Convoluciones 1D sólo deslizamos el kernel en una única dirección; izquierda/derecha en este diagrama.

Avanzado: una Convolución 1D no es lo mismo que una Convolución 1×1 2D.

Codificando las cosas

Sorprendentemente, necesitaremos un bloque Conv1D en Gluon para nuestra Convolución 1D. Definimos la forma del kernel como 3, y ya que estamos trabajando con un solo kernel en este ejemplo, especificaremos channels=1.

import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)

Ahora podemos pasar nuestra entrada al bloque conv usando un kernel predefinido.

input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>

¿Qué cambia con el relleno, la zancada y la dilatación?

Vimos el efecto del relleno, la zancada y la dilatación en el último post sobre Convoluciones 2D, y es muy similar para las Convoluciones 1D. Con el relleno, esta vez sólo rellenamos a lo largo de una sola dimensión (la dimensión temporal). Nuestro diagrama representa el tiempo a través del eje horizontal, así que rellenamos a la izquierda y a la derecha de los datos de entrada (y no por encima y por debajo como en el ejemplo de la Convolución 2D). Con el stride y la dilatación, sólo los aplicamos a lo largo de la dimensión temporal también. Por lo tanto, un ejemplo con relleno y dilatación sería el siguiente:

Agregamos dos argumentos adicionales en el código: padding=1 y strides=2.

conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>

Avanzado: las dimensiones de los datos de entrada deben ajustarse a un orden particular llamado layout. Por defecto, la convolución 1D espera ser aplicada a datos de entrada del formato ‘NCW’, es decir, tamaño del lote (N) * canales (C) * ancho/tiempo (W). Y para las Convoluciones 2D el formato por defecto es NCHW, es decir, tamaño de lote (N) * canales (C) * altura (H) * anchura (W). Compruebe el argumento layout de Conv1D y Conv2D.