Echa un vistazo a los artículos recientes

Abstract

La luz viaja por el vacío a una velocidad c independientemente del movimiento de la fuente de luz o del marco de referencia de un observador. En consecuencia, se requiere cierto tiempo para que la luz viaje desde una fuente de luz hasta un observador en el espacio, de manera que la emisión de luz y la observación de la luz emitida no son simultáneas. Basándose en estas consideraciones, se propone un método para medir la velocidad absoluta de un observador, que podría utilizarse para determinar el estado de movimiento de una nave espacial desde el interior de una cabina cerrada. En este estudio, también se introduce una nueva explicación de la transformación de Lorentz.

Palabras clave

sistema de coordenadas, sistema de referencia, movimiento, velocidad absoluta, relatividad, transformación de Lorentz, tiempo, espacio, observador, fuente de luz
El siguiente análisis presenta un enfoque práctico para medir la velocidad absoluta de un observador, que podría utilizarse para determinar el estado de movimiento de una nave espacial desde el interior de una cabina cerrada. El concepto de velocidad absoluta se refiere generalmente a una velocidad uniforme estándar de los diversos objetos de un sistema físico en relación con un espacio inmóvil postulado que existe independientemente de los objetos físicos contenidos en él (es decir, un espacio absoluto). Aquí presentamos un enfoque basado en la cinemática rígida para demostrar que la velocidad absoluta de un observador puede determinarse a partir del hecho de que la luz viaja a través del vacío con una velocidad c, independientemente del movimiento de la fuente de luz o del marco de referencia del observador. En consecuencia, se requiere cierto tiempo para que la luz viaje desde una fuente de luz hasta un observador en el espacio, de modo que la emisión de luz y la observación de la luz emitida no son simultáneas.
En el análisis propuesto, primero proporcionamos las siguientes convenciones para los sistemas de coordenadas considerados. Asumimos un sistema de coordenadas cartesianas compuesto por tres ejes perpendiculares a pares que se originan en el punto (0,0,0), donde cualquier punto P en el espacio puede definirse por sus coordenadas a lo largo de los ejes x, y y z, representados por un par ordenado de números reales (x,y,z). Se supone que un sistema de referencia inercial S está representado por un sistema de coordenadas rectangulares espaciales (x,y,z) cuyo origen es O. Una serie de relojes estándar (denominados relojes S) están situados en puntos estacionarios de S. Los relojes S se calibran mutuamente (es decir, proporcionan lecturas equivalentes en el mismo instante de tiempo) basándose en la transmisión y recepción de una señal luminosa. Específicamente, en el momento tA, se proyecta un haz de luz desde el reloj A hacia el reloj B, que luego es reflejado en el momento tB por el reloj B de vuelta hacia el reloj A, y llega al reloj A en el momento tA’. Si , los dos relojes están calibrados. Para cualquier suceso situado en las coordenadas x,y,z, su coordenada temporal t viene dada por la lectura del reloj S relacionado con el suceso. De forma similar, se establece otro sistema de referencia inercial S’ basado en un segundo sistema de coordenadas rectangulares espaciales (x’,y’,z’) cuyo origen es O’, y otra serie de relojes estándar mutuamente calibrados (relojes S’) se sitúan en puntos estacionarios del sistema de referencia S’. Para cualquier suceso situado en las coordenadas x’,y’,z’, su coordenada temporal t’ viene dada por la lectura del reloj S’ relacionado con el suceso.
Debido a que los respectivos orígenes de las coordenadas espaciales y temporales, así como las direcciones de los ejes de coordenadas pueden seleccionarse arbitrariamente en gran medida, las relaciones entre S y S’ empleadas aquí se basan en las siguientes convenciones, que se han aplicado por simplicidad.
(1) En un determinado instante de tiempo, los orígenes y los ejes de coordenadas de los dos sistemas se superponen, y los relojes situados respectivamente en O y O’ se ponen a cero, es decir .
(2) Los ejes x y x’ coinciden en la dirección del movimiento relativo de S y S’; así, x y x’ coinciden en todo momento, mientras que y e y’, así como z y z’ son paralelos.
(3) S’ se mueve a lo largo de la dirección +x de S.
El análisis propuesto se basa en el principio fundamental de que la luz en el vacío viaja a una velocidad constante c independientemente del movimiento del observador o de la fuente de luz. Por lo tanto, definimos aquí la velocidad absoluta U del observador, que se supone lineal y uniforme, como , donde f(φ) representa una función de la relación geométrica entre la dirección de una señal luminosa y la dirección de U, denotada aquí como φ.
En el análisis propuesto se proporcionan dos nuevas explicaciones de la relatividad del tiempo y la longitud, que difieren de las explicaciones de Einstein (véase «Sobre la electrodinámica de los cuerpos en movimiento»). Estas explicaciones se presentan en las siguientes secciones.

La relatividad del tiempo

Debido a la velocidad finita de la luz, se requiere cierto tiempo para que la luz viaje desde una fuente luminosa hasta un observador en el espacio. Por lo tanto, se puede deducir que la emisión de luz y la observación de la luz no pueden ser simultáneas. Partiendo de la constancia de la velocidad de la luz y de las condiciones ilustradas en la figura 1, definimos los siguientes factores. Las posiciones de una fuente de luz y de un observador en , en el momento en que la fuente de luz emite luz (denotado como evento R), se dan respectivamente como A y H0. Durante el período de propagación de la luz desde hasta , el observador recorre una distancia U∙T desde la posición H0 hasta H, donde recibe la luz emitida. En consecuencia, definimos como la distancia l entre la posición del observador al recibir la señal luminosa en y la posición de la fuente de luz cuando emite luz en . Debido a la constancia de la velocidad de la luz, . La distancia equivale a U∙T. Finalmente, definimos como la distancia l0 entre la posición del observador en y la posición de la fuente de luz en . Aquí introducimos una consideración de la posición del observador en , que anteriormente se pensaba que no tenía importancia física. Si los estados de movimiento del observador y de la fuente de luz son equivalentes, se da l0, de manera que U puede calcularse a través de las relaciones triangulares ilustradas en la ,Figura 1.
En el presente trabajo, el tiempo de un evento se mide utilizando el siguiente método. Tanto el observador como un reloj se sitúan en el origen. Cuando la señal luminosa que representa la ocurrencia de un evento llega al observador, la hora de llegada de la luz se corresponderá con la hora indicada por el reloj. La ventaja de esta correspondencia es que siempre está relacionada con la posición del observador que emplea el reloj. Como se ve en la figura 1, el punto espacial O3 puede definirse en base a la posición de la fuente de luz cuando emite luz en , y el punto espacial O2 puede definirse en base a la posición del observador cuando recibe luz en . Sin embargo, el medio para definir el punto espacial O1 en el que se encuentra el observador cuando la fuente de luz emite luz en no es obvio. Para resolver este problema, se introducen los conceptos de reposo absoluto (es decir, ) y movimiento absoluto (es decir, ). Sustituimos respectivamente el único observador en movimiento en H0 y H por dos observadores H1 y H2 en reposo en los puntos espaciales O1 y O2, respectivamente, mientras que la fuente de luz A está en reposo en el punto espacial O3. Cada uno de los observadores y la fuente de luz emplean relojes estándar calibrados, y A emite una señal luminosa en , denotada como evento R0. Cuando el observador H1 recibe la señal luminosa que viaja a c, la lectura del reloj es T0, y cuando la recibe H2, la lectura es T. De este modo, las distancias y pueden definirse en base a los respectivos tiempos de viaje de la señal luminosa como sigue:
, (1)
y
. (2)
De acuerdo con las relaciones triangulares mostradas en la Figura 1, la transformación del evento R0 entre los observadores H1 y H2 se da como sigue.
(3)
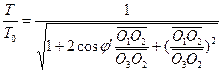(4)
Aquí, es el ángulo entre la línea O3O1 y el eje x, y es el ángulo entre la línea O3O2 y el eje x.
Volviendo ahora a la condición de un único observador en movimiento, suponemos que, en el sistema S, tanto el observador H como la fuente de luz A emplean un reloj estándar calibrado. En el instante del suceso R, la fuente de luz A está en el punto espacial O3, y el observador H está en O1. El instante en el que la señal luminosa llega al punto espacial O1 se corresponde con una lectura del reloj S de T0. Cuando el observador H recibe la señal luminosa, la lectura es T, y H está en O2.
Por supuesto, H no puede observar el evento R en el punto O1. Para resolver este problema, se coloca otro observador H- en el sistema S en el punto O1 correspondiente a , donde se emplea la posición de H- para definir el punto espacial O1. Entonces, la transformación del evento R entre los observadores H- y H puede obtenerse a través de la Ecuación (3) como sigue.
(5)
Por lo tanto, las ecuaciones (3) y (4) pueden reescribirse como sigue.
(6)
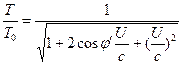(7)
e observa también que, para , las ecuaciones (6) y (7) se simplifican a lo siguiente.
(8)
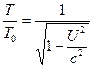(9)
Por lo tanto, basado en el análisis anterior, se puede obtener un método sencillo para determinar U a partir de la ecuación (6), dado que se conoce (φ).
Para simplificar, se elige como marco de referencia una fuente de luz con un estado de movimiento equivalente al de los observadores. Un observador se sitúa en el centro de una barra rígida recta en movimiento lineal uniforme, y las señales luminosas procedentes de diferentes posiciones de la barra llegan al observador en diferentes momentos. El observador detecta la desviación de la barra en la posición del observador con un ángulo de desviación que puede obtenerse a partir de la ecuación (8).
A través de este método, se puede determinar el estado de movimiento de una nave espacial desde una cabina cerrada.

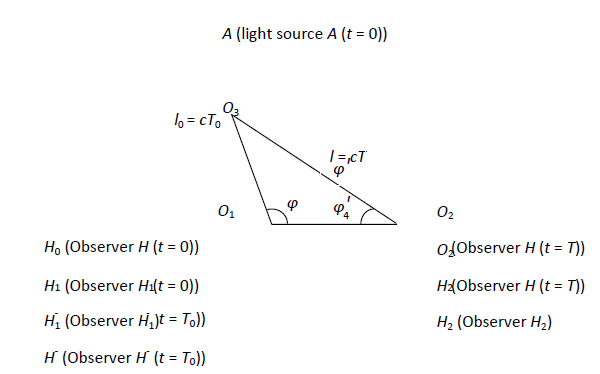
Figura 1: estados de movimiento del observador y de la fuente de luz

La relatividad de la longitud

En el análisis anterior, se han introducido dos longitudes, es decir, y . En este caso, se considera la longitud de una barra que se supone que es una barra rígida estacionaria de longitud L dentro de su sistema de coordenadas, para la cual L se mide con un calibre estacionario, y donde el eje de la barra coincide con el eje x de un sistema de coordenadas que se mueve con movimiento lineal uniforme a lo largo de la dirección +x con una velocidad absoluta U. Se supone que L se determina mediante las dos operaciones definidas a continuación.
(a) El observador reside en el mismo sistema de coordenadas en movimiento que la barra y el calibrador de pentagrama, y L se mide superponiendo la barra y el calibrador de pentagrama.
(b) Con la ayuda de varios relojes colocados en coordenadas estacionarias, que se mueven de forma sincronizada, el observador mide las posiciones de los dos extremos de la barra en coordenadas estacionarias en un momento específico t, y la distancia entre las dos posiciones se mide con el calibrador de pentagrama estacionario. es la longitud calculada a partir de la operación (a), que se denota aquí como la longitud de la barra en la coordenada móvil. es la longitud calculada a partir de la operación (b), que se denota aquí como la longitud de una barra en movimiento en la coordenada estacionaria. Es obvio que y son diferentes.
Suponemos que, en el sistema S, el observador H- está en el mismo estado de movimiento que H. Entonces, como se muestra en la Figura 1, H- está en el punto O1 cuando recibe la señal luminosa en , y, simultáneamente, el observador H está en el punto O4. Por lo tanto, t=0,04
es la distancia entre H- y H en , y
. (10)
es la distancia recorrida por el observador H en el intervalo de T0 a T, tal que
. (11)
es la distancia entre H- en y H en , tal que
. (12)
Como tal, se puede deducir la siguiente expresión.
(13)
A continuación, consideraremos las transformaciones de coordenadas y tiempo entre dos sistemas de coordenadas en movimiento, los cuales se mueven con una velocidad lineal uniforme, lo que representa una nueva explicación de la transformación de Lorentz.
Suponiendo que el observador H (en el sistema S), el observador H’ (en el sistema S’), y la fuente de luz A» (en el sistema S») emplean relojes estándar calibrados individualmente, y, en , la fuente de luz A» emite una señal luminosa, denotada como evento R». En el instante del evento R», A» está en el punto O3, y los observadores H y H’ coinciden. Cuando el observador H recibe la señal luminosa, la lectura del reloj S es T, y H está en el punto O1. Cuando el observador H’ recibe la señal luminosa, la lectura del reloj S’ es T’, y H’ está en el punto O2. Entonces, la transformación del evento R» entre los observadores H’ y H puede calcularse a partir de la ecuación (3), donde
. (14)
Aquí, u es la velocidad relativa entre los observadores H’ y H, lo que produce las siguientes transformaciones.
(15)
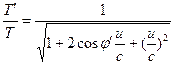(16)
De se pueden derivar las siguientes relaciones:
. (17)
Cuando y , la ecuación (16) se simplifica a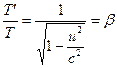
. (18)
Por lo tanto, se pueden deducir las siguientes relaciones de transformación:
, (19)
, (20)
, (21)
. (22)
Además, cuando ,
, (23)
y
, (24)
, (25)
, (26)
. (27)