El procedimiento de sustracción para la eliminación del PL se elaboró por primera vez hace unas dos décadas. Este procedimiento no afecta a los componentes del ECG vecinos a la frecuencia de PL. Este estudio teórico se realiza para la frecuencia básica del PL, pero las conclusiones son también válidas para sus armónicos y, en consecuencia, para una forma de onda de interferencia arbitraria. La eficacia del procedimiento no depende de la amplitud de la interferencia, siempre que el amplificador no esté saturado. Además, el procedimiento se adapta con éxito a los cambios de amplitud y frecuencia de la interferencia. El procedimiento se ha mejorado continuamente a lo largo de los años, y se ha implementado en miles de instrumentos de ECG y sistemas asistidos por ordenador. Otros investigadores también han publicado enfoques similares.
- Principios
- Compensación de las variaciones de amplitud del PL
- Filtrado lineal
- Compensación de la variación de la frecuencia del PL
- Evaluación de la eficacia del procedimiento
- Influencia del ruido de la EMG
- Supresión de interferencias en ECG de alta resolución
- Caso de los dispositivos suministrados por baterías y los sistemas de ECG asistidos por ordenador
- Adaptación automática a la frecuencia nominal de PL
- Desarrollo del procedimiento teórico
Principios
El procedimiento de sustracción se aplica originalmente con la frecuencia de muestreo f S , un múltiplo de, y el hardware sincronizado con la frecuencia PL f PL . El procedimiento consta de los siguientes pasos :
-
Los segmentos de ECG con banda de frecuencia cercana a cero se detectan continuamente utilizando un criterio apropiado. Se denominan segmentos lineales y se encuentran principalmente en los intervalos PQ y TP, pero también en partes rectas suficientemente largas de las ondas R y T.
-
Las muestras de estos segmentos se promedian en movimiento, es decir, se someten a un filtro de peine de fase lineal con el primer cero fijado en f PL . Así, las muestras filtradas no contienen interferencias.
-
Las amplitudes de las interferencias, denominadas correcciones, se calculan para cada una de las muestras de fase bloqueada, n, en el periodo PL, T PL , restando las muestras filtradas de las correspondientes de la señal ECG contaminada (original).
-
El conjunto de correcciones obtenidas se actualiza continuamente en los segmentos lineales y se utiliza en los segmentos no lineales (normalmente alrededor de los complejos QRS y de las ondas T de gran amplitud) para restar la interferencia de la señal de ECG original.
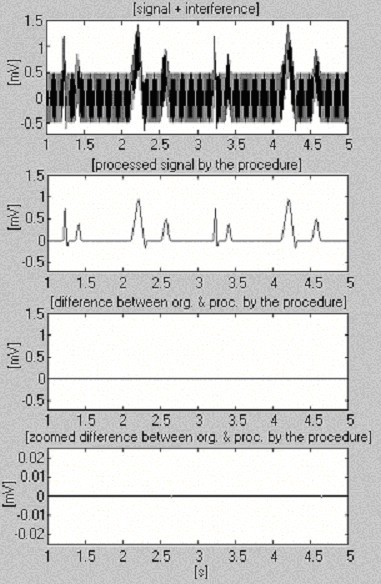
Uno de los primeros resultados obtenidos por el método de sustracción se muestra en la Fig. 1 . Se añadieron interferencias a una señal de ECG limpia simulada para evaluar los errores y la eficacia del método.
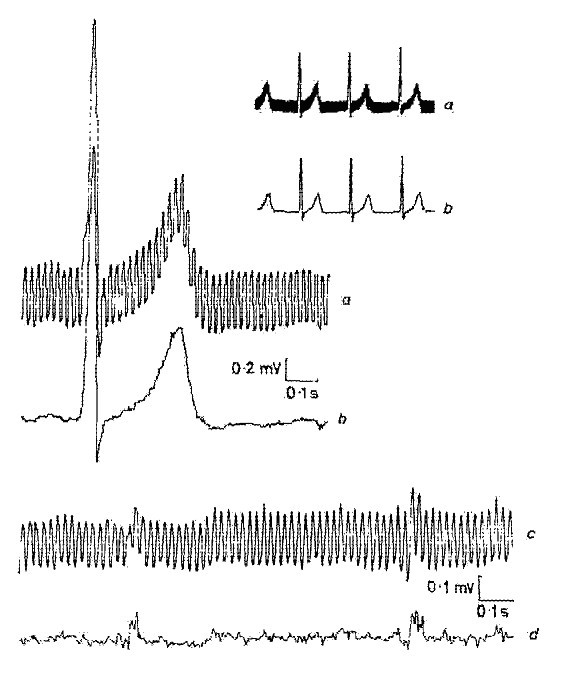
Uno de los primeros resultados obtenidos por el procedimiento de sustracción.
Criterio lineal
Un criterio lineal, Cr, suele corresponder a la segunda diferencia de la señal (evaluación matemática de la linealidad). El primer Cr se define de la siguiente manera. Se calculan seis primeras diferencias consecutivas, FD i , utilizando muestras de señal, X i , espaciadas a un T PL :
FD i = X i+n – X i , para i = 1 … 6 (1)
La interferencia PL en las primeras diferencias se suprime si n = f S /f PL . En este caso n = 5, ya que el procedimiento se desarrolló inicialmente para f PL = 50 Hz y f S = 250 Hz. Además, se toman los valores máximo FD max y mínimo FD min para determinar Cr:
Cr = | FD max – FD min | <M, (2)
donde M es el valor del umbral.
En la Fig. 2 se muestran segmentos lineales y no lineales típicos. La señal de ECG real (trazo a) está superpuesta por la interferencia (trazo b). Los segmentos lineales incluyen la señal de baja frecuencia y los componentes de frecuencia de la línea eléctrica. En la Fig. 3 se muestra un espectro de frecuencia aproximado de dichos segmentos lineales.

Segmentos lineales y no lineales típicos en la señal de ECG real.
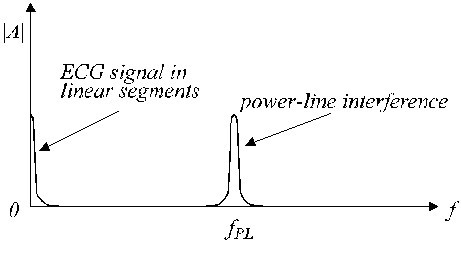
Espectro de frecuencias aproximado de un segmento lineal.
Este criterio funciona con precisión, pero apenas puede aplicarse en tiempo real debido a su implementación relativamente lenta. Este inconveniente es superado por Christov y Dotsinsky que utilizan un criterio modificado de sólo dos diferencias posteriores.
Cr = | FDi+1- FD i | <M. (3)
La primera muestra, que no cumple la ecuación (3), está asociada al inicio de un segmento no lineal. En la transición de no lineal a lineal, la ecuación (3) debe cumplirse consecutivamente n veces para evitar la detección prematura del segmento lineal. El criterio se aplica en tiempo real para f S = 400 Hz y n = 8.
Más tarde, Dotsinsky y Daskalov definieron el criterio como dos diferencias no consecutivas:
Cr = |FDi+k- FD i | <M, para k >1 (4)
Este enfoque hace más precisa la transición de segmento lineal a no lineal.
Compensación de las variaciones de amplitud del PL
Cuanto más frecuentemente se actualicen las correcciones, mejor será la compensación de las variaciones de amplitud del PL. Por lo tanto, el umbral del criterio lineal, M, tiene que ser razonablemente menos restrictivo para que los errores, cometidos al promediar algunos segmentos que se apartan de la señal lineal ideal, sean menores que los errores, que aparecerán si M inicia la actualización esporádica de la corrección. Inicialmente, M se fijó en 160 μV . Posteriormente, se encontraron valores heurísticos de M = 150 μV y M = 100 μV .
Filtrado lineal
Para un número de muestra impar n = 2m + 1 en un periodo de la interferencia PL, el valor filtrado:
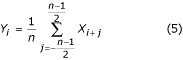
es coincidente en fase con el no filtrado.
En el caso de un número par n = 2m, los dos valores están desplazados en fase por la mitad del período de la muestra:
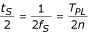
pero se convierten en una coincidencia en fase utilizando la fórmula
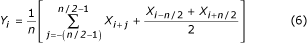
Es posible tomar para promediar cada segunda, tercera o qmuestra si n/q es entero. Dependiendo de si n/q es par o impar, se utiliza la ecuación (7) o (8), respectivamente.

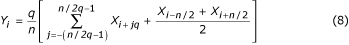
Un caso especial de reducción máxima de la muestra surge con q = n/2 . La fórmula correspondiente:
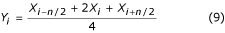
se llama filtro de tres puntos. Además de la ecuación (8), también se puede aplicar la siguiente fórmula
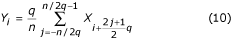
si q es par. En el caso de q = n/2, el filtro se convierte en ‘dos puntos’ y se representa por:

La reducción del número de muestras en un período de la interferencia dará lugar a una mayor pendiente de los lóbulos del filtro en peine y acortará el tiempo de cálculo. Sin embargo, estas «ventajas» deben evaluarse cuidadosamente para no violar la regla de Nyquist con una gran cantidad del tercer armónico presente. Los demás armónicos no se tienen en cuenta, ya que los armónicos impares más altos suelen suprimirse mediante filtros de paso bajo con corte en el rango de 100-150 Hz, mientras que los pares están prácticamente ausentes debido a la fabricación precisa de los polos de los generadores de las centrales eléctricas.
Compensación de la variación de la frecuencia del PL
La desviación permitida de la frecuencia nominal del PL está limitada en algunos países hasta el 1% por las normas. En la práctica, la desviación suele ser mayor. Kumaravel et al. informaron de una variación del 3%. McManus et al. encontraron cambios considerables en la frecuencia de interferencia, que se superpone a las grabaciones tomadas de la base de datos Common Standards for Electrocardiography (CSE).
Las variaciones de frecuencia conducen a un caso especial de muestreo no múltiple con n real, en lugar de uno entero. Esta complicación puede obviarse si las desviaciones se detectan mediante la medición continua por hardware de f PL y se corrigen mediante pequeños ajustes del intervalo de muestreo t S en torno a su valor nominal (R), t RS = T RPL /n (aquí, T RPL = 20 ms es el T PL nominal para f RPL = 50 Hz). Para f PL , desviación entre 49,5 y 50,1 Hz, las variaciones de t S están en el rango del 1%, y en consecuencia no introducen errores más allá de la precisión de medición aceptada de los parámetros que se suelen utilizar para la clasificación automática del ECG.
Una primera aproximación asocia el disparo de cada primera muestra, S 1 , de las secuencias S k (k = 1, 2…n) en los periodos T PL con amplitud elegida arbitrariamente pero constante de la tensión PL. Las siguientes muestras, S k (k = 2…n), se espacian en t S , que se obtiene por t S = T RTL /n. Para 50 Hz, y n = 5, t S = 4 ms. Dotsinsky y Daskalov estudian dos tipos de errores cometidos con este enfoque. El primero, debido a las irregularidades entre muestras, puede alcanzar el 1% a f S = 400 Hz y el 1,2% a f S = 250 Hz, en caso de desviación del 1% en torno a la f RPL . El segundo tipo de error no supera el 3% y es consecuencia de la ubicación adicionalmente desplazada de la muestra filtrada.
Dotsinsky y Daskalov informaron de un enfoque mejorado. El período en curso T PL se mide y se divide por n. El t S obtenido se utiliza en el T PL posterior.
Evaluación de la eficacia del procedimiento
Los ejemplos del procedimiento de sustracción se muestran en la Fig. 4 y la Fig. 5. Las señales de ECG se toman de la base de datos de la American Heart Association. Las señales son filtradas con notch para suprimir las interferencias de 60 Hz (frecuencia del PL en los Estados Unidos). A continuación, las señales se mezclan con interferencias de 50 Hz, moduladas en amplitud de 0 a 3,2 mVp-p mediante una velocidad de giro de 200 μVs-1. Las trazas se identifican como sigue: i) señal de entrada; ii) interferencia sintetizada; iii) señal mezclada; iv) señal procesada; v) diferencia entre las señales original y procesada y vi) diferencia ampliada. En realidad, los componentes descartados también incluyen ruidos electromiográficos (EMG) y otros. Una parte no suprimida de la señal, junto con pequeñas interferencias residuales y distorsiones debidas al compromiso con el valor M también están presentes en las diferencias.
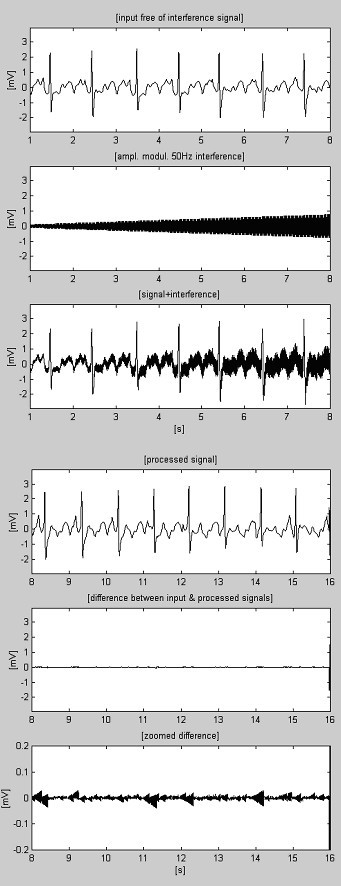
Registro AHA 3004d1 procesado.
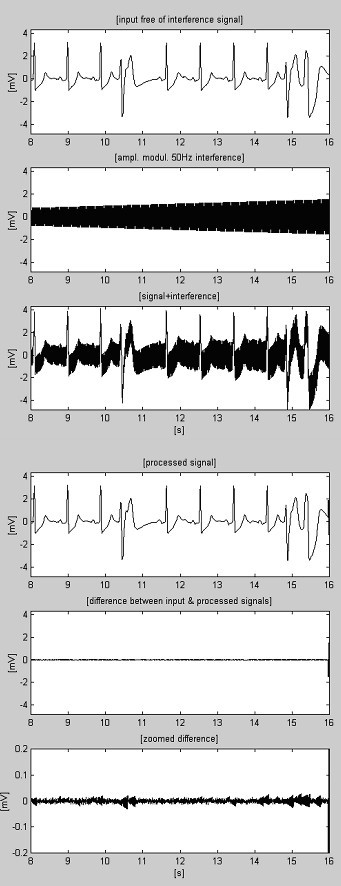
Grabación AHA 6007d1 procesada.
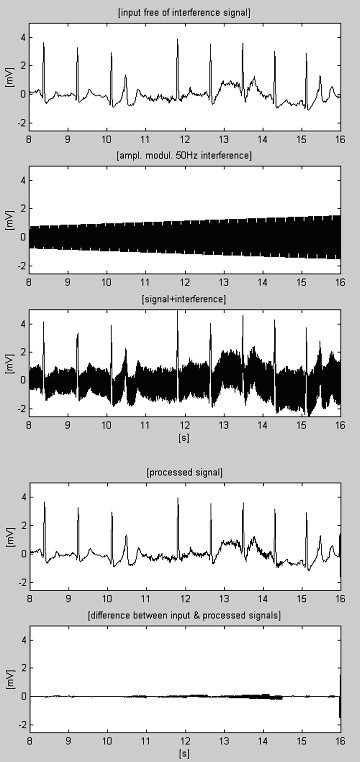
Se utilizan dos señales para evaluar la eficacia del procedimiento de sustracción con respecto a la interferencia solamente. La primera, tomada de nuestra propia base de datos, se denomina condicionalmente «limpia» (Fig. 6). El resultado muestra pequeñas diferencias entre las señales de entrada y las procesadas, debido visualmente al ruido presentado en la entrada. Este resultado se verifica con la segunda señal sintetizada, que no contiene ninguna perturbación (Fig. 7). Como puede verse, no se introducen distorsiones. La misma señal sintetizada se superpone con interferencias y se procesa (Fig. 8). No se encuentra ninguna interferencia residual.
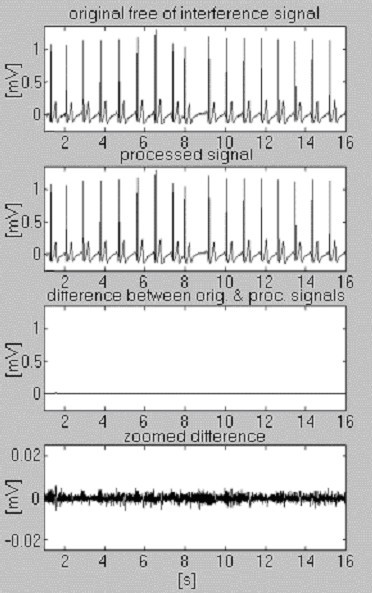
Procesamiento de la señal condicionalmente «limpia».
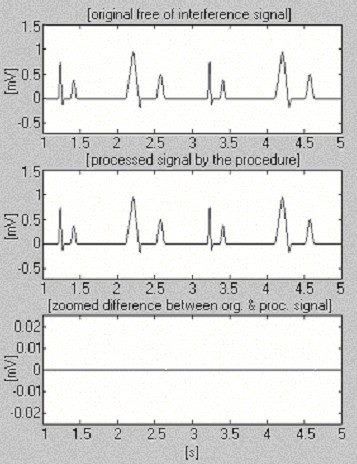
Procesamiento de la señal sintetizada.
Procesamiento de señal sintetizada+interferencia.
Influencia del ruido de la EMG
A veces el ruido de la EMG es tan alto que el hallazgo del segmento lineal se ve obstaculizado. Como consecuencia, las correcciones inexactas, que no se corresponden con el último cambio de la amplitud de interferencia, provocarán errores (véase el ruido residual entre el 11º y el 14º s en la Fig. 9).
Señal ECG procesada+ruido EMG+interferencia.
Un enfoque muy simple para la supresión de la influencia del ruido EMG en el procedimiento introduce un buffer paralelo adicional donde las porciones en curso de la señal se promedian incondicionalmente . Este búfer se utiliza para la detección precisa de la linealidad. La Fig. 10 y la Fig. 11 muestran la comparación de los resultados sin y con el buffer paralelo. Los trazos ‘a’ representan la señal de ECG mezclada con interferencia y ruido EMG. Las trazas ‘b’ en la Fig. 10 y ‘c’ en la Fig. 11 indican las transiciones de segmentos lineales a no lineales (funciones on-off). Como puede verse, la parte de la señal promediada en la Fig. 10 es muy limitada. En consecuencia, la eficacia del procedimiento es reducida (Fig. 10c y 10d. En cambio, el buffer paralelo permite detectar segmentos lineales largos (Fig. 11c y el ruido residual en la señal procesada (Fig. 11d es bajo. Sin embargo, el ruido no se suprime totalmente porque una parte de él participa en el cálculo de la corrección.
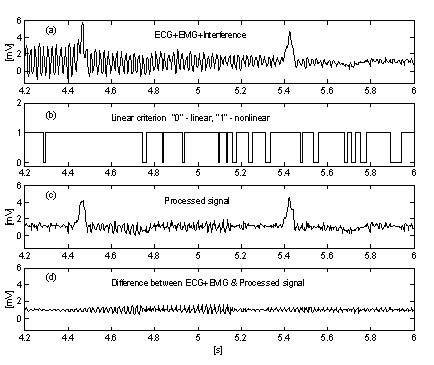
Sustracción del ruido de interferencia+EMG sin buffer paralelo.
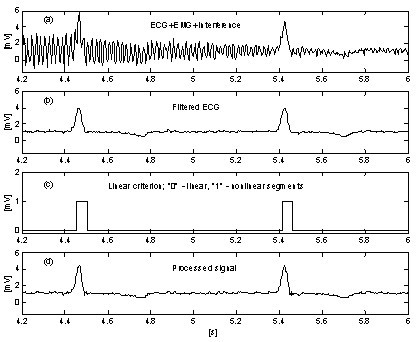
Substracción de interferencia+ruido EMG con buffer paralelo.
Una mejora adicional en la supresión del ruido EMG la obtiene Christov utilizando el valor de umbral adaptativo M, que se calcula con respecto a la relación ruido/señal Rt, definida como Rt = S NL /S F , donde el nivel de ruido S NL es igual a la anchura resumida de los segmentos no lineales en una época S F , que corresponde aproximadamente al intervalo RR considerado. La búsqueda de linealidad con un criterio de M = 150 μV para un ECG «limpio» (Fig. 12a) y para la misma señal, pero contaminada con ruido EMG (Fig. 12b) muestran diferentes S NL , (Fig. 12c y 12d). El método se desarrolla en el entorno MATLAB. El umbral inicial M se elige igual a 30 μV. Luego, se incrementa gradualmente hasta que Rt alcanza el 10%, tras lo cual se inicia el procedimiento de sustracción. El nivel Rt ≤ 0,1 valor es sugerido por la relación ‘anchura del QRS frente a su intervalo RR’, que suele estar en torno al 10%. La eliminación tanto de las interferencias como del ruido EMG puede observarse en las Fig. 13b y 13d, donde se utiliza M = 420 μV. Para comparar, la señal de ECG ‘limpia’ se procesa con M = 35 μV (Fig. 13a y 13c).

Niveles de ruido SNL (trazos c y d) en la señal de ECG ‘limpia’ (trazo a) y la señal contaminada por EMG (trazo b), respectivamente.
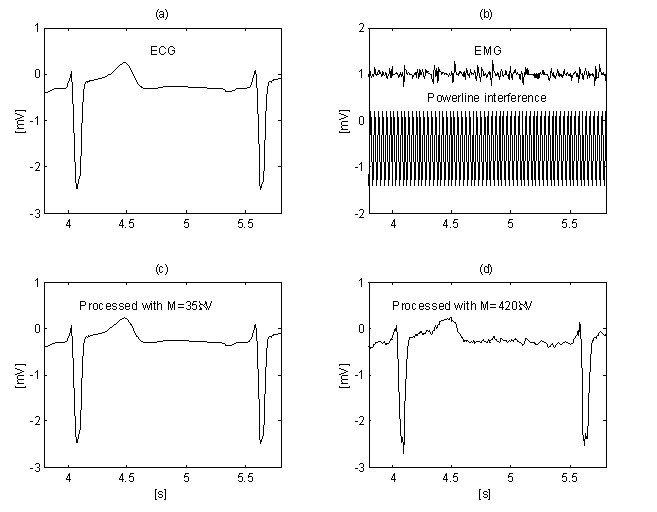
Supresión de ruido de interferencia+EMG mediante umbral adaptativo M: ‘señal limpia’ (a) procesada con M = 35 μV (c) y señal contaminada (b) sometida al procedimiento con M = 420 μV (d).
Los segmentos lineales no pueden encontrarse regularmente en pacientes con fibrilación auricular y ventricular. Sin embargo, la preservación total de la forma de la onda no es necesaria para la detección de la fibrilación y, por lo tanto, pueden aplicarse todo tipo de filtros tradicionales.
Supresión de interferencias en ECG de alta resolución
El procedimiento de sustracción no es directamente aplicable al His-ECG de superficie corporal, ya que la onda His de baja amplitud y relativamente baja frecuencia no puede distinguirse en segmentos lineales. Por lo tanto, la onda de His será, en la práctica, suprimida o incluso eliminada de la señal. El ruido del EMG suele ser de mayor amplitud y con un contenido de frecuencia mucho más alto en comparación con la onda de His superficial. Por lo tanto, el simple cambio del valor del umbral, M, no da como resultado una delineación aceptable de los segmentos lineales y no lineales.
Bazhina et al. implementaron la siguiente modificación. El inicio del segmento no lineal detectado antes de un complejo QRS se desplaza 100 ms hacia la izquierda, definiendo así la región de la onda His como un segmento no lineal por defecto (Fig. 14).
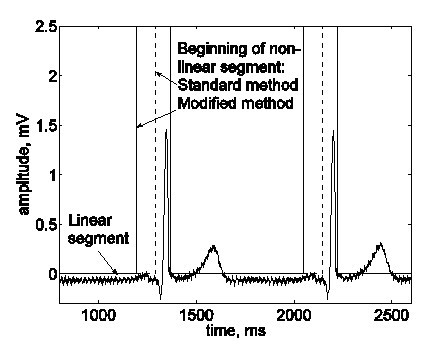
El inicio de un segmento no lineal que incluye el complejo QRS se desplazó por defecto 100 ms hacia la izquierda, para incluir la zona donde se espera que aparezca la onda de His.
El procedimiento de sustracción y otros tres métodos: filtros de muesca, interpolación espectral y sustracción de regresión se prueban frente a una distorsión mínima de la señal original . Los procedimientos de sustracción y de regresión-sustracción resultaron ser los mejores, ya que Baratta et al. utilizan un concepto similar para la estimación del ruido en segmentos lineales. La regresión-sustracción trata mal los cambios de amplitud de la interferencia dentro del segmento actual.
Caso de los dispositivos suministrados por baterías y los sistemas de ECG asistidos por ordenador
La medición por hardware de f PL , necesaria para la compensación de la modulación de frecuencia de la interferencia, no es factible en los dispositivos suministrados por baterías y en algunos sistemas de ECG asistidos por ordenador. Dotsinsky y Stoyanov estudiaron el rango de cambios de frecuencia de la interferencia con amplitud constante, para el cual la parte residual se restringe a niveles aceptables sin utilizar el muestreo sincronizado. Descubrieron que se podía obtener una interferencia residual inferior a 20 μVp-p con el procedimiento de: i) amplitud de interferencia ≤ 0,4 mVp-p y ii) cambio de frecuencia con una tasa ≤ 0,0125 Hzs-1. Dado que estos requisitos para la fuente de alimentación pueden superarse a menudo, se desarrolló un software de medición de interferencias.
La señal de ECG se procesa inicialmente mediante un filtro de paso de banda de 49-51 Hz. Se miden las amplitudes de dos muestras adyacentes, Br L y Br R , tomadas de una pendiente positiva de la interferencia, situadas por debajo y por encima de la línea cero (Fig. 15). La distancia, t CP , entre el punto de cruce CP y la muestra derecha, Br R , se calcula continuamente mediante:
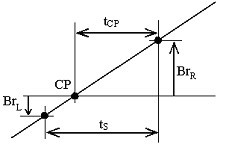
Cruce del cero de interferencia.

En caso de cambio de T PL, t S se redefine utilizando

Este enfoque se implementó en el entorno MATLAB. Para la frecuencia de muestreo f S = 500 Hz y f RPL = 50 Hz, n es igual a 10. El producto kn determina el tiempo que se recomienda que transcurra antes de calcular y sustituir el nuevo tCP,i + kn por el anterior tCP,i. La Fig. 16 muestra una señal de ECG de 1 mV procesada después de haber sido mezclada por interferencias con una amplitud constante de 2 mVp-p y una variación extremadamente rápida de 1 Hz por 8 s de frecuencia (primer trazo). Para evaluar la eficacia obtenida, se presenta también la diferencia ampliada sin muestreo sincronizado (último trazo).
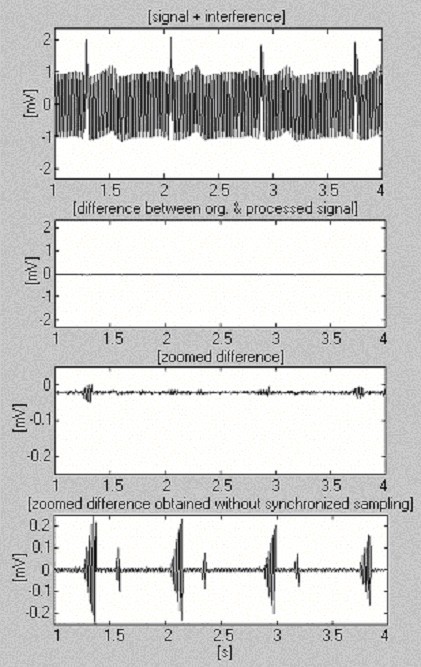
Procedimiento de sustracción mediante medición de la frecuencia de la línea eléctrica por software.
El siguiente paso lógico a realizar consiste en: i) mantener la t S nominal del instrumento de ECG, ii) volver a muestrear la señal según la f PL medida en curso para eliminar las interferencias y iii) volver a la t S nominal. Los primeros resultados de este enfoque son muy prometedores. Así, la compensación por software de la variable f PL , así como una implementación total del procedimiento de sustracción en un instrumento, incluyendo el ajuste automático para f RPL de 50 o 60 Hz, se completará independientemente de los circuitos de hardware y el software correspondiente.
Adaptación automática a la frecuencia nominal de PL
Un programa común para la sustracción alternativa de interferencias en un entorno de 50 y 60 Hz conduce a un muestreo no múltiple, es decir, a un n real. Los valores ampliamente utilizados de t S para f RPL = 50 Hz, como 250, 500 y 1000 Hz, corresponden a un n irracional de 4,1(6), 8,3(3) y 4,1(6) si hay que eliminar las interferencias de 60 Hz. En el caso inverso, f S = 360 Hz requiere n = 7,2. Es inaceptable utilizar valores redondeados n*, ya que introducirían un error considerable.
Una solución muy sencilla que no necesita el cambio de f S fue encontrada por Dotsinsky y Stoyanov . El procedimiento original aplica un filtro de peine sobre un período, T PL , de la interferencia. Así, el programa se ejecuta más rápidamente. Generalmente, n puede tomarse de k > 1 períodos enteros. El procedimiento funciona si:
n = kT PL /t S es un número entero.
Para t S = 2 ms (f S = 500 Hz) y f RPL = 50 Hz, el menor valor de k que satisface la ecuación (14) es realmente k = 1. Sin embargo, en el caso de 60 Hz, k es igual a 3. Los ceros asociados a los subarmónicos 20 y 40 Hz aparecerán también, pero no influyen en el procedimiento. Por lo tanto, basta con cambiar n entre 10 (k = 1) y 25 (k = 3) para operar con ambas interferencias. Para ello, dos filtros digitales de paso de banda controlan la señal entrante. La Fig. 17 muestra que el filtro con banda de frecuencia que se solapa con la interferencia genera una señal de salida de un orden de magnitud mayor que el otro filtro.
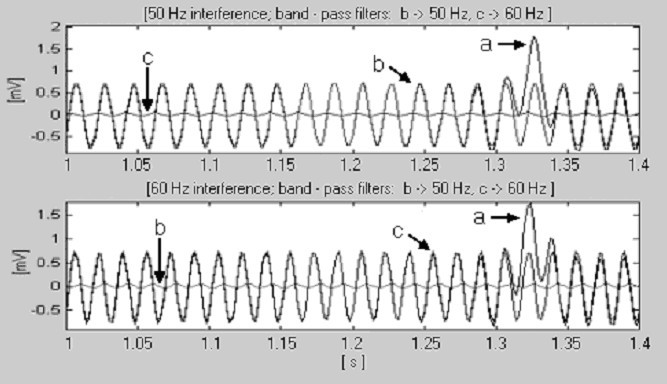
Detección de la frecuencia nominal de la línea eléctrica, a) parte del complejo QRS, b) interferencia de 50 Hz y c) interferencia de 60 Hz.
Desarrollo del procedimiento teórico
La teoría del procedimiento de sustracción fue desarrollada posteriormente por Mihov , Levkov y Mihov , y Mihov et al. Propusieron cuatro tipos de filtros, implementados en una estructura generalizada que puede superar los problemas con casi todos los casos de muestreo no múltiple, incluyendo las variaciones de frecuencia de interferencia, sin utilizar la conversión AD sincronizada.
El llamado filtro D en muestreo múltiple se define como es Cr en la ecuación (2), donde la segunda diferencia, D i , se obtiene con FD s que están espaciados a un T PL :
D i = (X i+n – X i ) – (X i – X i-n ) = X i-n – 2X i + X i+n (15)
La función de transferencia del filtro D tiene ceros en f = 0 y f = f PL Hz, que se muestra igual a 50 Hz en la Fig. 18.

Función de transferencia del filtro D para fPL = 50 Hz.
El filtro K describe la media móvil presentada por las ecuaciones (5) y (6). Su función de transferencia se da en la Fig. 19 para n = 5 en caso de multiplicidad impar.
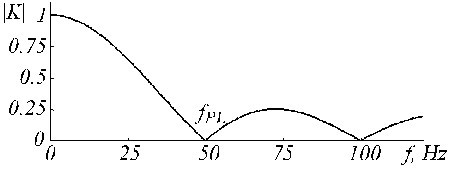
Función de transferencia del filtro K para fPL = 50 Hz y n = 5.
La ecuación utilizada para el cálculo continuo de las componentes de interferencia:
B i = X i – Y i (16)
define en realidad un filtro digital denominado (1-K)-filtro.
Además, los filtros se redefinen para el muestreo no múltiple, y se toma en consideración f S = 250 Hz junto con f RPL = 60 Hz para ilustrar la mejora del software.
Para preservar los ceros de la función de transferencia, el filtro D debe restarse con un filtro de corrección con cero en f = 0 y ganancia de D RPL en f = f RPL , igual a la ganancia del filtro D para la misma frecuencia, f RPL . La síntesis del filtro de corrección se basa en un filtro auxiliar de tres puntos dado por la ecuación:

donde (n/2)* es el valor redondeado de n/2.
Como A RPL es la ganancia del filtro auxiliar para f = f RPL , el filtro de corrección se multiplica por la relación D RPL /A RPL . Utilizando las funciones de transferencia correspondientes, D RPL y A RPL se calculan de antemano mediante:
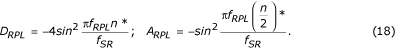
Finalmente, el filtro D* corregido se presenta como

y se muestra en la Fig. 20 mediante la traza ‘c’, donde las trazas ‘a’ y ‘b’ son el filtro D y el filtro de corrección, respectivamente.
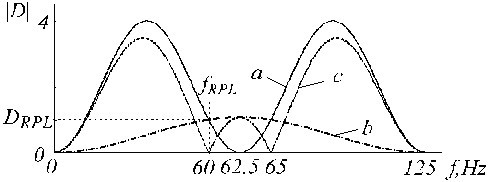
Funciones de transferencia de a) filtro D, b) filtro de corrección auxiliar y c) filtro D corregido.
La función de transferencia del filtro K debe conservar el cero para f = f RPL , la ganancia unitaria para f = 0 y la respuesta de fase lineal. El procedimiento de corrección del filtro K es similar al anterior. Un filtro auxiliar viene dado por la fórmula utilizada para el cálculo de las correcciones:
A i = X i – Y i , (20)
La ganancia del filtro es igual a 1 – K RPL para f = f RPL , donde K RPL es la ganancia del filtro K para la misma frecuencia f RPL . El filtro auxiliar se multiplica por K RPL /(1 – K RPL ) y se resta del filtro K. La ecuación del filtro K* corregido es:
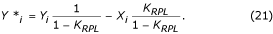
La constante K RPL puede estimarse mediante:

para la multiplicidad par o impar, respectivamente.
Un ejemplo de corrección del filtro K se muestra en la Fig. 21, donde las trazas ‘a’, ‘b’ y ‘c’ representan el filtro K primario, el filtro auxiliar y el filtro K* corregido.
Función de transferencia de a) filtro K, b) filtro auxiliar de corrección y c) filtro K corregido.
En el caso de un muestreo no múltiple, aparece una diferencia de fase entre las muestras de ECG en curso y los componentes de interferencia B i (ecuación 16) que suelen estar situados en un búfer temporal del tipo «primero en entrar, primero en salir» (FIFO). Por lo tanto, B i debe modificarse restándose de las muestras de ECG durante los segmentos no lineales. El procedimiento de compensación es relativamente complicado. La Fig. 22 muestra el contenido del buffer temporal. La muestra de interferencia actual, B i-n *, no coincide con la muestra restaurada, B i . Su amplitud debe ser recalculada para compensar la diferencia de fase entre ellas. Esto se consigue mediante un nuevo filtro con respuesta de fase lineal y ganancia unitaria para f = f RPL , denominado filtro B. Se sintetiza a partir del filtro K conocido, con una ventana igual al periodo de interferencia. En caso de n* impar, puede describirse como:
Valores recuperados en el buffer temporal.
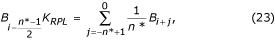
donde K RPL es la ganancia de la interferencia del filtro de promediación dada por la ecuación (22).
El valor restaurado del buffer B i puede calcularse mediante:
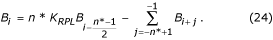
En caso de n* par:
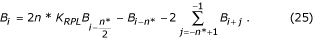
La función de transferencia del filtro B se muestra en la Fig. 23.
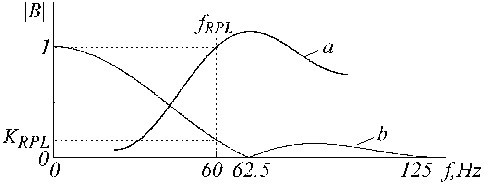
Funciones de transferencia de a) el filtro B y b) el conocido filtro K.
La estructura generalizada se presenta en la Fig. 24, donde los módulos del procedimiento de sustracción son los siguientes:
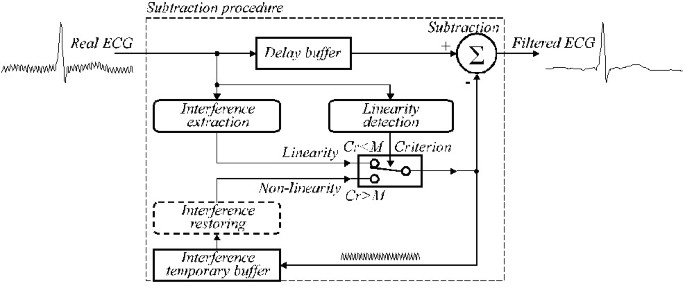
Estructura generalizada del procedimiento de sustracción.
-
Detección de linealidad. Se aplica el filtro D para evaluar la linealidad de cada vecindad de muestras de señal.
-
Extracción de interferencias. Se utiliza el filtro (1-K) para calcular el componente de interferencia.
-
Criterio. La condición Cr <M envía la interferencia PL extraída o restaurada a Subtraction.
-
Interference temporary buffer. La componente de interferencia extraída o restaurada utilizada como corrección en el segmento no lineal se guarda en la posición bloqueada con la fase en curso de la interferencia de línea eléctrica.
-
Restauración de la interferencia. Se llama al filtro B en caso de muestreo no múltiple para restablecer los verdaderos valores de corrección, que deben restarse de las muestras de la señal de entrada en los segmentos no lineales.
-
Buffer de retardo. Compensa el retardo, que aparece con el filtro D y el filtro (1-K) y es imprescindible si el procedimiento se ejecuta en tiempo cuasi-real. De lo contrario, el búfer podría no tenerse en cuenta.
-
Substracción. El valor de interferencia extraído o restaurado se resta de la señal de entrada retardada para obtener una señal de ECG «limpia». En caso de no linealidad, tanto la extracción de la interferencia como la sustracción implementan el filtro K.
Se ha probado off-line un algoritmo mejorado según la estructura generalizada. Los resultados para f S = 250 Hz y f RPL = 60 Hz se muestran en la Fig. 25.
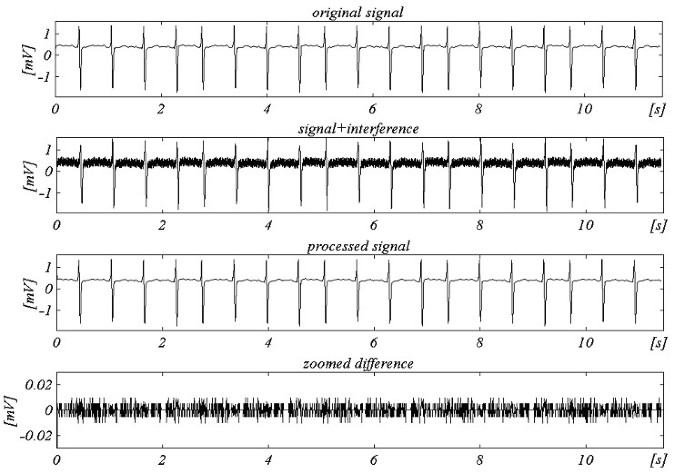
Ejemplo para un muestreo no múltiple con fRPL = 60 Hz y fS = 250 Hz.