Grupo abeliano | CDhistory

Un grupo abeliano es un grupo cuyos elementos se conmutan (es decir, para todos los elementos y ). Los grupos abelianos corresponden, por tanto, a grupos con tablas de multiplicación simétricas.

Todos los grupos cíclicos son abelianos, pero un grupo abeliano no es necesariamente cíclico. Todos los subgrupos de un grupo abeliano son normales. En un grupo abeliano, cada elemento está en una clase de conjugación por sí mismo, y la tabla de caracteres implica potencias de un solo elemento conocido como generador de grupo.

En Wolfram Language, la función AbelianGroup representa el producto directo de los grupos cíclicos de grados , , ….

No se conoce ninguna fórmula general para dar el número de grupos finitos no isomórficos de un orden de grupo dado. Sin embargo, el número de grupos finitos abelianos no isomorfos de cualquier orden de grupo dado se da escribiendo como

(1)

donde los son factores primos distintos, entonces

(2)

donde es la función de partición, que se implementa en Wolfram Language como FiniteAbelianGroupCount. Los valores de para , 2, … son 1, 1, 1, 2, 1, 1, 1, 3, 2, … (OEIS A000688).

Los órdenes más pequeños para los que existen , 2, 3, … grupos abelianos no isomorfos son 1, 4, 8, 36, 16, 72, 32, 900, 216, 144, 64, 1800, 0, 288, 128, … (OEIS A046056), donde 0 denota un número imposible (es decir, no es un producto de números de partición) de grupos abelianos no isomorfos. Los valores «perdidos» son 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41, 43, 46, … (OEIS A046064). Los números incrementalmente mayores de los grupos abelianos en función del orden son 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, … (OEIS A046054), que se dan para los órdenes 1, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, … (OEIS A046055).

El teorema de descomposición de Kronecker establece que todo grupo abeliano finito puede escribirse como un producto directo de grupo de grupos cíclicos de orden de grupo de potencia primera. Si el orden de grupo de un grupo finito es un primo , entonces existe un único grupo abeliano de orden (denotado ) y ningún grupo no abeliano. Si el orden del grupo es un primo al cuadrado , entonces hay dos grupos abelianos (denotados y . Si el orden del grupo es un primo al cubo , entonces hay tres grupos abelianos (denotados , , y ), y cinco grupos en total. Si el orden es un producto de dos primos y , entonces existe exactamente un grupo abeliano de orden (denotado ).

Otro resultado interesante es que si denota el número de grupos abelianos no isomorfos de orden de grupo , entonces

(3)

donde es la función zeta de Riemann.

Los números de grupos abelianos de órdenes vienen dados por 1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15, 17, 18, 19, 20, 25, … (OEIS A063966) para , 2, …. Srinivasan (1973) también ha demostrado que

(4)

donde

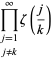			(5)
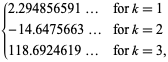			(6)

(OEIS A021002, A084892, y A084893) y es de nuevo la función zeta de Riemann. Nótese que Richert (1952) dio incorrectamente . Las sumas también pueden escribirse en las formas explícitas