Intervalos de tolerancia
Esta sección contiene detalles estadísticos para los intervalos de tolerancia de un lado y de dos lados.
Intervalos basados en la distribución normal
Intervalo unilateral
El intervalo unilateral se calcula de la siguiente manera:
Límite inferior = 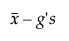
Límite superior = 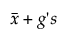
donde
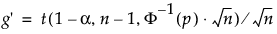
s es la desviación estándar
t es el cuantil de la distribución nodistribución central t
Φ-1 es el cuantil normal estándar
Intervalo de dos lados
El intervalo de dos lados se calcula como sigue:
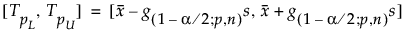
donde s es la desviación estándar y g(1-α/2; p,n) es una constante.
Para determinar g, considere la fracción de la población capturada por el intervalo de tolerancia. Tamhane y Dunlop (2000) dan esta fracción como sigue:
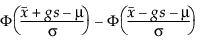
donde Φ denota la cdf (función de distribución acumulativa) normal estándar.
Por tanto, g resuelve la siguiente ecuación:
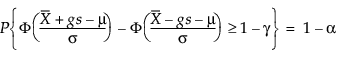
donde 1 – γ es la fracción de todas las observaciones futuras contenidas en el intervalo de tolerancia.
Para más información sobre los intervalos de tolerancia basados en la distribución normal, véanse las tablas J.1a, J.1b, J.6a y J.6b de Meeker et al. (2017).
Intervalos no paramétricos
Límite inferior unilateral
El límite inferior de tolerancia unilateral del 100(1 – α)% para contener al menos una proporción β de la distribución muestreada de una muestra de tamaño n es el estadístico de orden x(l). El índice l se calcula como sigue:
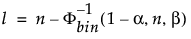
donde Φ-1bin(1-α, n, β) es el (1 – α)º cuantil de la distribución binomial con n ensayos y probabilidad de éxito β.
El nivel de confianza real se calcula como Φbin(n-l, n, β), donde Φbin(x, n, β) es la probabilidad de que una variable aleatoria distribuida binomialmente con n ensayos y probabilidad de éxito β sea menor o igual que x.
Nótese que para calcular un intervalo de tolerancia inferior sin distribución unilateral, el tamaño de la muestra n debe ser al menos tan grande como 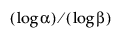 .
.
Límite superior unilateral
El límite superior de tolerancia unilateral del 100(1 – α)% para contener al menos una proporción β de la distribución muestreada de una muestra de tamaño n es el estadístico de orden x(u). El índice u se calcula como sigue:
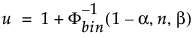
donde Φ-1bin(1-α, n, β) es el (1 – α)º cuantil de la distribución binomial con n ensayos y probabilidad de éxito β.
El nivel de confianza real se calcula como Φbin(u-1, n, β), donde Φbin(x, n, β) es la probabilidad de que una variable aleatoria distribuida binomialmente con n ensayos y probabilidad de éxito β sea menor o igual que x.
Nótese que para calcular un intervalo de tolerancia superior libre de distribución unilateral, el tamaño de la muestra n debe ser al menos tan grande como 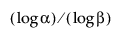 .
.
Intervalo de dos lados
El intervalo de tolerancia de dos lados del 100(1 – α)% para contener al menos una proporción β de la distribución muestreada de una muestra de tamaño n se calcula como sigue:
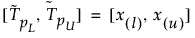
donde x(i) es el estadístico de orden ith y l y u se calculan como sigue:
Sea ν = n – Φ-1bin(1-α, n, β), donde Φ-1bin(1-α, n, β) es el (1 – α)º cuantil de la distribución binomial con n ensayos y probabilidad de éxito β. Si ν es menor que 2, no se puede calcular un intervalo de tolerancia sin distribución de dos lados. Si ν es mayor o igual que 2, l = floor(ν/2) y u = floor(n + 1 – ν/2).
El nivel de confianza real se calcula como Φbin(u-l-1, n, β), donde Φbin(x, n, β) es la probabilidad de que una variable aleatoria distribuida binomialmente con n ensayos y probabilidad de éxito β sea menor o igual que x.
Nótese que para calcular un intervalo de tolerancia sin distribución de dos lados, el tamaño de la muestra n debe ser al menos tan grande como el n de la siguiente ecuación:

Para más información sobre los intervalos de tolerancia sin distribución, véase Meeker et al. (2017, sección 5.3).