Reconstrucción 3D

En esta práctica se pretende programar la lógica necesaria para que el robot kobuki pueda generar una reconstrucción 3D de la escena que está recibiendo a través de sus cámaras izquierda y derecha.

Instalación

Instalar la Infraestructura General de la Academia de Robótica JdeRobot.

¿Cómo ejecutar su solución?

Navega hasta el directorio 3d_reconstruction

cd exercises/3d_reconstruction

Lanza Gazebo con el mundo kobuki_3d_reconstruction a través del comando

roslaunch ./launch/3d_reconstruction_ros.launch

Luego tienes que ejecutar la aplicación académica, que incorporará tu código:

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

¿Cómo realizar el ejercicio?

Para realizar el ejercicio, tienes que editar el fichero MyAlgorithm.py e insertar en él tu código, que reconstruye puntos 3d a partir de las dos vistas estereoscópicas.

¿Dónde insertar el código?

En el archivo MyAlgorithm.py,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Interfaz de programación de aplicaciones

• self.getImage('left') – para obtener la imagen izquierda
• self.getImage('right') – para obtener la imagen derecha
• self.point.PlotPoint(position, color) – para trazar el punto en la herramienta 3d

Navegar por la interfaz GUI

Basado en el ratón: Mantener y arrastrar para moverse por el entorno. Desplazamiento para acercarse o alejarse

Basado en el teclado: Teclas de flecha para moverse por el entorno. Teclas W y S para acercarse o alejarse

Teoría

En visión por ordenador y gráficos por ordenador, la reconstrucción 3D es el proceso de determinar el perfil 3D de un objeto, así como conocer la coordenada 3D de cualquier punto del perfil. La reconstrucción se puede lograr de la siguiente manera:

• Basada en el hardware: El enfoque basado en el hardware requiere que utilicemos el hardware específico para la tarea de reconstrucción. El uso de luz estructurada, telémetro láser, medidor de profundidad y métodos radiométricos son algunos ejemplos.

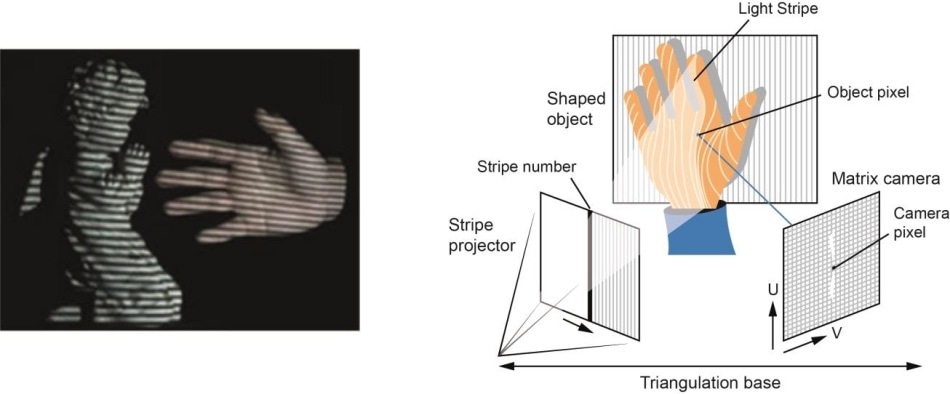
• Basado en software: El enfoque basado en software se basa en la capacidad de cálculo del ordenador para determinar las propiedades 3D del objeto. La forma a partir del sombreado, la textura, la visión estereoscópica y la homografía son algunos buenos métodos.

En este ejercicio nuestro principal objetivo es llevar a cabo la reconstrucción 3D utilizando el enfoque basado en software, en particular la reconstrucción 3D por visión estereoscópica.

Geometría epipolar

Cuando dos cámaras ven una escena 3D desde dos posiciones diferentes, hay una serie de relaciones geométricas entre los puntos 3D y sus proyecciones sobre las imágenes 2D que conducen a restricciones entre los puntos de la imagen. El estudio de estas propiedades y restricciones se denomina Geometrías Epipolares. La imagen y la explicación siguiente pueden generalizar la idea:

Supongamos que un punto X en el espacio 3d es imaginado en dos vistas, en x en la primera y x' en la segunda. Retroproyectando los rayos a sus centros de cámara a través de los planos de la imagen, obtenemos una superficie plana, denotada por π.

Suponiendo ahora que sólo conocemos x, podemos preguntarnos cómo se constriñe el punto correspondiente x'. El plano π está determinado por la línea base (línea que une los centros de las cámaras) y el rayo definido por x. Por lo anterior, sabemos que el rayo correspondiente al punto desconocido x' se encuentra en π, por lo que el punto x' se encuentra en la línea de intersección l' de π con el segundo plano de la imagen. Esta línea se llama línea epipolar correspondiente a x. Esta relación nos ayuda a reducir el espacio de búsqueda del punto en imagen derecha, de un plano a una recta. Algunas definiciones importantes a tener en cuenta son:

• El epipolo es el punto de intersección de la línea que une los centros de la cámara (la línea base) con el plano de la imagen.

• Un plano epipolar es un plano que contiene la línea base.

• Una línea epipolar es la intersección del plano epipolar con el plano de la imagen.

Reconstrucción estereoscópica

La reconstrucción estereoscópica es un caso especial de la reconstrucción 3d anterior en el que los dos planos de la imagen son paralelos entre sí e igualmente distantes del punto 3d que queremos trazar.

En este caso la línea epipolar para ambos planos de la imagen son iguales, y son paralelos a la anchura de los planos, simplificando mejor nuestra restricción.

Algoritmo de reconstrucción 3D

El algoritmo de reconstrucción consta de 3 pasos:

1. Detectar los puntos de característica en un plano de la imagen
2. Detectar el punto de característica correspondiente al encontrado anteriormente
3. Triangular el punto en el espacio 3d

Veamos uno por uno

Detección de puntos de característica

La detección de puntos de característica es un vasto campo de estudio en el que ya se estudian varios algoritmos. Los algoritmos Harris Corner Detection y Shi-Tomasi utilizan valores propios para obtener un buen punto de característica. Pero, el problema es que necesitamos muchos puntos para la Reconstrucción 3D, y estos algoritmos no podrán proporcionarnos un número tan grande de puntos de característica.

Por lo tanto, utilizamos puntos de borde como nuestros puntos de característica. Puede haber ambigüedad en su detección en la siguiente etapa del algoritmo. Pero, nuestro problema se resuelve tomando los bordes como puntos de característica. Un detector de bordes muy bueno es el algoritmo de detección de bordes Canny. El algoritmo es bastante simple y fiable en términos de generación de los bordes.

Extracción de puntos de característica

El uso de la restricción epipolar realmente simplifica la complejidad de tiempo de nuestro algoritmo. Para los problemas generales de reconstrucción 3D, tenemos que generar una línea epipolar para cada punto en un fotograma de la imagen, y luego buscar en ese espacio de muestra el punto correspondiente en el otro fotograma de la imagen. La generación de la línea epipolar es también muy fácil en nuestro caso, es sólo la iterpolación de la línea paralela de la imagen izquierda al plano de la imagen derecha.

Comprobar la correspondencia entre las imágenes implica muchos algoritmos, como la Suma de Diferencias Cuadradas o la Minimización de Energía. Sin profundizar mucho, el uso de un simple filtro de Correlación también es suficiente para nuestro caso de uso.

Triangulación

La triangulación, en términos sencillos, no es más que calcular dónde va a estar el punto 3d utilizando los dos puntos determinados en los planos de la imagen.

En la realidad, la posición de los puntos de la imagen no se puede medir con exactitud. En el caso de las cámaras generales, puede haber distorsiones geométricas o físicas. Por lo tanto, hay mucha matemática detrás de la minimización de ese error y el cálculo de la proyección de puntos 3d más precisa. Consulte este enlace para ver un modelo sencillo.

Pistas

Pistas sencillas proporcionadas para ayudarle a resolver el ejercicio de 3d_reconstrucción. Para este ejercicio se utiliza mucho la librería OpenCV.

Setup

Usando la API del ejercicio, podemos recuperar las imágenes fácilmente. Además, después de obtener las imágenes, es una buena idea realizar un filtrado bilateral en las imágenes, porque hay algunos detalles adicionales que no necesitan ser incluidos durante la reconstrucción 3d. Revise las ilustraciones para ver los efectos de realizar el filtrado bilateral.

Calcular Correspondencias

OpenCV ya tiene filtros de correlación incorporados que pueden ser llamados a través de matchTemplate(). Cuida los casos extremos como bordes y esquinas.

Una buena observación es que los puntos de la izquierda tendrán correspondencia en la parte izquierda y los puntos de la derecha tendrán correspondencia en la parte derecha. Usando esta observación, podemos acelerar fácilmente el cálculo de la correspondencia.

Planificar los puntos

Tanto la función manual como la basada en OpenCV triangulatePoints funcionan bien para la triangulación. Solo hay que tener cuidado con todas las formas y tamaños de las matrices mientras se realizan las implementaciones algebraicas.

Tenga en cuenta la diferencia entre coordenadas 3D simples y coordenadas 4D homogéneas. Mira este video para más detalles. Simplemente dividiendo el vector 4d completo por su 4ª coordenada nos da las coordenadas 3d.

Debido a las variadas implementaciones de los usuarios, el usuario puede tener que ajustar la escala y el desplazamiento de los puntos triangulados para hacerlos visibles y representables en la interfaz GUI. La reducción de la escala del vector de coordenadas 3D en un valor entre 500 y 1000 funciona bien. También funciona bien un desplazamiento de 0 a 8.

Ilustraciones