La troisième loi postule que l’entropie d’une substance est toujours finie et qu’elle s’approche d’une constante lorsque la température s’approche de zéro. La valeur de cette constante est indépendante des valeurs de toutes les autres fonctions d’état qui caractérisent la substance. Pour toute substance donnée, nous sommes libres d’attribuer une valeur choisie arbitrairement à la valeur limite de la température zéro. Cependant, nous ne pouvons pas attribuer des entropies zéro-température arbitraires à toutes les substances. L’ensemble des attributions que nous faisons doit être cohérent avec les valeurs limites à zéro température des changements d’entropie des réactions entre les différentes substances observées expérimentalement. Pour les substances parfaitement cristallines, ces entropies de réaction sont toutes nulles. Nous pouvons satisfaire cette condition en attribuant une valeur arbitraire à l’entropie molaire à température zéro de chaque élément et en stipulant que l’entropie à température zéro de tout composé est la somme des entropies à température zéro de ses éléments constitutifs. Ce calcul est grandement simplifié si l’entropie à température zéro de chaque élément est nulle. C’est le contenu essentiel de la troisième loi.
L’énoncé de Lewis et Randall intègre cette sélection de l’état de référence à entropie nulle pour les entropies, en le spécifiant comme « un état cristallin » de chaque élément à zéro degré. Par conséquent, l’entropie de toute substance à zéro degré est supérieure ou égale à zéro. En d’autres termes, la déclaration de Lewis et Randall inclut une convention qui fixe la valeur limite de l’entropie de toute substance à zéro degré. À cet égard, la déclaration de Lewis et Randall fait un choix essentiellement arbitraire qui n’est pas une propriété intrinsèque de la nature. Nous voyons, cependant, que c’est un choix extrêmement commode.
Nous avons discuté des énoncés alternatifs des première et deuxième lois. Un certain nombre d’énoncés alternatifs de la troisième loi sont également possibles. Nous considérons les suivants :
Il est impossible d’atteindre une température de zéro absolu.
Cet énoncé est plus général que celui de Lewis et Randall. Si nous considérons l’application de cette affirmation aux températures atteignables dans les processus impliquant une seule substance, nous pouvons montrer qu’elle implique, et est impliquée par, l’affirmation de Lewis et Randall.
Les propriétés de la capacité thermique, \(C_P\), jouent un rôle central dans ces arguments. Nous avons vu que \(C_P\) est une fonction de la température. Bien qu’il ne soit pas utile de le faire, nous pouvons appliquer la relation de définition de \(C_P\) à une substance subissant une transition de phase et trouver \(C_P=\infty\). Si nous pensons à une substance dont la capacité thermique est inférieure à zéro, nous rencontrons une contradiction dans nos idées de base sur la chaleur et la température : Si \(q>0\) et \({q}/{\Delta T}<0\), nous devons avoir \(\Delta T<0\) ; c’est-à-dire que le chauffage de la substance entraîne une diminution de sa température. En bref, la théorie que nous avons développée embarque des prémisses qui exigent \(C_P>0\) pour tout système sur lequel nous pouvons faire des mesures.
Caractérisons un système de substance pure par sa pression et sa température et considérons des processus réversibles à pression constante dans lesquels seul le travail pression-volume est possible. Alors \({\gauche({\partiel S}/{partiel T}\droite)}_P={C_P}/{T}\) et \(dS={C_PdT}/{T}\). Nous voulons maintenant montrer que la stipulation de Lewis et Randall selon laquelle l’entropie est toujours finie exige que la capacité thermique devienne nulle lorsque la température devient nulle. (Comme nous allons montrer que la troisième loi interdit les mesures au zéro absolu, cette conclusion est cohérente avec notre conclusion du paragraphe précédent). Le fait que la capacité thermique devienne nulle lorsque la température devient nulle est évident d’après \(S={C_PdT}/{T}.\) Si \(C_P\) ne devient pas nulle lorsque la température devient nulle, \(dS\) devient arbitrairement grande lorsque la température devient nulle, ce qui contredit l’affirmation de Lewis et Randall.
Pour développer ce résultat de manière plus explicite, nous laissons les capacités thermiques aux températures \(T\) et zéro être \(C_P\left(T\right)\) et \(C_P\left(0\right)\), respectivement. Puisque \(C_P\left(T\right)>0\) pour tout \(T\ >\ 0\), nous avons \(S\left(T\right)-S\left(T^*\right)>0\) pour tout \(T>T^*>0\). Puisque l’entropie est toujours finie, \(\infty >S\left(T\right)-S\left(T^*\right)>0\\), de sorte que
\\\\ }>0\]
et
\
Pour des températures au voisinage de zéro, nous pouvons développer la capacité thermique, avec une précision arbitraire, comme un polynôme en série de Taylor en \(T\) :
Les inégalités deviennent
La condition de gauche requiert \(C_P\left(0\right)=0\).
Nous pourrions considérer la troisième loi comme une déclaration sur les capacités thermiques des substances pures. Nous déduisons non seulement que \(C_P>0\) pour tout \(T>0\), mais aussi que
\
De manière plus générale, nous pouvons déduire les assertions correspondantes pour les systèmes réversibles fermés qui ne sont pas des substances pures : \({\left({\partial H}/{\partial T}\right)}_P>0\) pour tout \(T>0\), et \({\mathop{\mathrm{lim}}_{T\to 0} T^{-1}{\left({\partial H}/{\partial T}\right)}_P=0\\). (Cependant, les entropies à température zéro de ces systèmes ne sont pas nulles). Dans la discussion ci-dessous, nous décrivons le système comme une substance pure. Nous pouvons utiliser les mêmes arguments pour n’importe quel système ; il suffit de remplacer \(C_P\) par \({\gauche({\partiel H}/{partiel T}\droite)}_P\). L’énoncé de Lewis et Randall affirme que l’entropie devient constante au zéro absolu, quelles que soient les valeurs des autres fonctions thermodynamiques. Il s’ensuit que l’entropie à zéro degré est indépendante de la valeur de la pression. Pour deux pressions quelconques, \(P_1\) et \(P_2\), nous avons \(S\left(P_2,0\right)-S\left(P_1,0\right)=0\). En admettant que \({P=P}_1\) et \(P_2=P+\Delta P\) et, nous avons
\
pour tout \(\Delta P\). Par conséquent, nous avons
\
Dans le chapitre 10, nous trouvons \({\gauche({\partiel S}/{\partiel }P\right)}_T=-{\gauche({\partiel V}/{\partiel T}\right)}_P\), donc l’entropie et le volume approchent tous deux leurs valeurs de température zéro de manière asymptotique.
Quand nous disons que le zéro absolu est inatteignable, nous voulons dire qu’aucun système ne peut subir de changement dans lequel sa température finale est nulle. Pour voir pourquoi le zéro absolu doit être inatteignable, considérons les processus qui peuvent diminuer la température d’un système. En général, nous disposons de réservoirs de chaleur à différentes températures. Nous pouvons choisir le réservoir disponible dont la température est la plus basse, et amener le système à cette température par simple contact thermique. Ce point est trivial ; le défi consiste clairement à réduire davantage la température. Pour ce faire, nous devons effectuer un autre changement. Quel que soit ce changement, il ne peut être favorisé par un échange de chaleur avec l’environnement. Une fois que nous avons amené le système à la température de la partie la plus froide de l’environnement, tout autre échange de chaleur avec l’environnement ne peut être que contre-productif. Nous en concluons que tout processus adapté à notre objectif doit être adiabatique. Puisqu’un processus adiabatique n’échange aucune chaleur avec l’environnement, \(\Delta \hat{S}=0\).
Le processus doit également être un processus possible, de sorte que \(\Delta S+\Delta \hat{S}\ge 0\), et puisqu’il est adiabatique, \(\Delta S\ge 0\). Considérons un processus réversible et un processus irréversible dans lesquels le même système\({}^{2}\) passe de l’état spécifié par \(P_1\) et \(T_1\) à un second état dans lequel la pression est \(P_2\). Les températures finales et les changements d’entropie de ces processus sont différents. Pour le processus réversible, \(\Delta S=0\) ; nous désignons la température finale par \(T_2\). Pour le processus irréversible, \(\Delta S>0\) ; nous désignons la température finale par \(T^*_2\). Il s’avère que le changement de température est moins important pour le processus irréversible que pour le processus réversible ; c’est-à-dire que \(T_2-T_1<t^*_2-t_1\)>. De manière équivalente, le processus réversible atteint une température plus basse : \({T_2<t}^*_2\)>. De
\
nous pouvons calculer les changements d’entropie pour ces processus. Pour le processus réversible, nous calculons \
Pour ce faire, nous calculons d’abord
\
pour la transformation réversible isotherme de l’état \(P_1\), \(T_1\) à l’état spécifié par \(P_2\) et \(T_1\). Pour cette étape, \(dT\) est zéro, et donc
\
Nous calculons ensuite
\
pour la transformation réversible isobare de l’état \(P_2\), \(T_1\) à l’état \(P_2\), \(T_2\). Pour cette transformation, \(dP\) est nul, et
\
Alors,
\
Parce que \(\Delta S^{rev}=0\), le processus réversible est unique ; c’est-à-dire, étant donné \(P_1\), \(T_1\), et \(P_2\), la température finale du système est déterminée. Nous trouvons \(T_2\) à partir de
\
Pour comprendre le changement d’entropie pour le processus irréversible, nous notons d’abord qu’il existe un nombre infini de tels processus. La température finale n’a rien d’unique. Étant donné \(P_1\), \(T_1\), et \(P_2\), la température finale, \(T^*_2\), peut avoir n’importe quelle valeur compatible avec les propriétés de la substance. Pour spécifier un processus irréversible particulier, nous devons spécifier les quatre quantités : \(P_1\), \(T_1\), \(P_2\), et \(T^*_2\). Ceci étant fait, nous pouvons calculer la variation d’entropie pour le processus irréversible,
\
en calculant les variations d’entropie lorsque nous transportons de manière réversible le système le long du chemin isotherme en deux étapes de \(P_1\), \(T_1\) à \(P_2\), \(T_1\) et ensuite le long du chemin isobarique de \(P_2\), \(T_1\) à \(P_2\), \(T^*_2\). Le calcul de \(\Delta S^{irrev}\) pour ce chemin réversible de \(P_1\), \(T_1\) à \(P_2\), \(T^*_2\) utilise la même logique que le calcul, dans le paragraphe précédent, de \(\Delta S\) pour le chemin réversible de \(P_1\), \(T_1\) à \(P_2\), \(T_2\). La différence est que \(T^*_2\) remplace \(T_2\) comme limite supérieure dans l’intégrale de température. L’intégrale de pression est la même. Nous avons
\
D’après \(\Delta S^{irrev}>\Delta S^{rev}\), nous avons
\
Puisque les intégrandes sont les mêmes et positives, il s’ensuit que \(T^*_2>T_2\), comme affirmé ci-dessus.
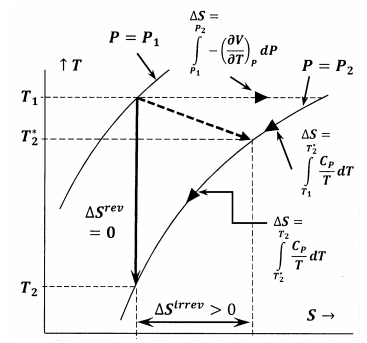
La figure 6 montre les relations entre les différentes quantités discutées dans cet argument. Dans le premier cas, la figure 6 montre un tracé de deux des isobares du système dans l’espace température-entropie. En d’autres termes, la ligne intitulée \(P=P_1\) représente l’ensemble des points de température-entropie auxquels le système en équilibre a une pression \(P_1\) ; la ligne intitulée \(P=P_2\), représente les positions d’équilibre à la pression \(P_2\). Les autres lignes de ce croquis représentent les chemins le long desquels le système peut subir des changements réversibles à entropie constante ou à température constante. La ligne en pointillé représente le processus irréversible dans lequel le système passe de l’état spécifié par \(P_1\), \(T_1\) à l’état spécifié par \(P_2\), \(T^*_2\). Cette ligne est en pointillé pour représenter le fait que la température du système peut ne pas être bien définie pendant le processus irréversible.
Un refroidissement efficace peut être réalisé en utilisant des changements de pression si le système est un gaz. Cependant, pour les liquides et les solides, \({\gauche({\partiel V}/{\partiel T}\droite)}_P\) est faible ; par conséquent, le changement de température pour un changement de pression réversible est également faible. À des températures proches du zéro absolu, presque toutes les substances sont solides ; pour obtenir un refroidissement efficace, nous devons modifier une variable thermodynamique pour laquelle le coefficient de température d’un solide est aussi grand que possible. Pour étudier le problème général de la diminution de la température d’un système en faisant varier autre chose que la pression, nous devons considérer un système dans lequel une certaine forme de travail non lié à la pression et au volume est possible. Un tel système est soumis à une force supplémentaire, et son énergie change lorsque cette force change.
Démagnétisation adiabatique
La méthode pratique par laquelle des températures extrêmement basses sont atteintes est appelée démagnétisation adiabatique. Cette méthode exploite les propriétés des solides paramagnétiques. Dans ces solides, les électrons non appariés localisés sur des atomes individuels donnent naissance à un moment magnétique. La mécanique quantique permet de tirer des conclusions importantes sur l’interaction entre ces moments magnétiques et un champ magnétique appliqué : Dans un champ magnétique appliqué, le moment magnétique d’un atome individuel est quantifié. Dans le cas le plus simple, il ne peut être aligné que dans deux directions : il doit être soit parallèle, soit antiparallèle au champ magnétique appliqué. Lorsque le moment magnétique d’un atome est parallèle au champ magnétique, l’énergie du système est moindre que lorsque l’alignement est antiparallèle. Le champ magnétique appliqué exerce une force sur les moments magnétiques associés aux atomes individuels. L’énergie du système dépend de l’amplitude du champ magnétique appliqué.
Plutôt que de nous concentrer sur le cas particulier de la désaimantation adiabatique, considérons les changements d’énergie et d’entropie associés aux changements d’un potentiel généralisé, \({\mathit{\Phi}}_{\theta }\), et de son déplacement généralisé, \(\theta\). (Pour une désaimantation adiabatique, \(\theta\) serait le champ magnétique appliqué). Trois variables sont nécessaires pour décrire les changements réversibles dans ce système. Nous pouvons exprimer l’énergie et l’entropie comme des fonctions de la température, de la pression et de \(\theta\):
\(E=E\left(T,P,\theta \right)\) et \(S=S\left(T,P,\theta \right)\). La différentielle totale de l’entropie comprend un terme qui précise la dépendance de l’entropie par rapport à \(\theta\). Nous avons
\
où nous écrivons \(C\left(T,P,\theta \right)\) pour souligner que nos objectifs actuels exigent maintenant que nous mesurions la capacité thermique à pression constante et \(\theta\) constante.
Pour une pression constante, P, et un déplacement constant, \(\theta\), l’entropie dépend de la température comme
Le postulat selon lequel l’entropie est finie à toute température implique que la capacité thermique dépendante de la pression et du \(\theta\) devient nulle au zéro absolu. Autrement dit, au zéro absolu, la capacité thermique disparaît quelles que soient les valeurs de P et de \(\theta\). L’argument est exactement le même que précédemment. Auparavant, nous avons écrit \(C_P\left(0\right)=0\) ; pour le cas généralisé actuel, nous écrivons \(C\left(0,P,\theta \right)=0\).
De même, du postulat que l’entropie passe à une constante au zéro absolu pour toutes les valeurs des autres variables thermodynamiques, il résulte que, pour deux pressions quelconques \(P_1\) et \(P_2\), et pour deux valeurs quelconques du déplacement généralisé, \({\theta }_1\) et \({\theta }_2\),
\
et donc que
\ et \
Nous voulons considérer un processus dans lequel un système passe de la plus basse température disponible dans l’environnement à une température encore plus basse. Pour minimiser la température finale, ce processus doit être réalisé de manière adiabatique. Il doit également s’agir d’un processus possible, de sorte que \(dS\ge 0\). Pour simplifier, supposons maintenant que nous effectuons ce processus à une pression constante, \(P\), et que le système passe de l’état spécifié par \(P\), \(T_1\), \({\theta }_1\) à l’état spécifié par \(P\), \(T_2\), \({\theta }_2\) où \(T_1>T_2\). Les entropies de ces deux états sont
\ et \
La variation d’entropie pour ce processus est
\ \
Maintenant, supposons que la température finale soit nulle ; c’est-à-dire que \(T_2=0\), de sorte que
\ Il s’ensuit que \
où l’inégalité à droite découle du fait que \(C\left(T,P,{\theta }_1\right)>0\). Alors, il s’ensuit que
\
ce qui contredit l’énoncé de Lewis et Randall de la troisième loi. L’hypothèse selon laquelle le système peut atteindre le zéro absolu conduit à une contradiction de l’énoncé de Lewis et Randall de la troisième loi. Par conséquent, si l’énoncé de Lewis et Randall est vrai, le zéro absolu est inatteignable.
L’inverse s’applique également ; c’est-à-dire qu’à partir de la proposition que le zéro absolu est inatteignable, on peut montrer que l’énoncé de Lewis et Randall est vrai. Pour ce faire, nous réarrangeons l’équation ci-dessus pour \(\Delta S\),
\ \
Si nous supposons maintenant que l’affirmation de Lewis et Randall est fausse, l’expression de droite peut être inférieure ou égale à zéro. L’intégrale de gauche peut alors être nulle, auquel cas le système peut atteindre le zéro absolu. Si l’affirmation de Lewis et Randall est fausse, il est vrai que le système peut atteindre le zéro absolu. Par conséquent : Si le système ne peut pas atteindre le zéro absolu, l’affirmation de Lewis et Randall est vraie.
Les figures 7 et 8 illustrent ces idées à l’aide de courbes de niveau dans l’espace température-entropie. Chaque figure montre deux courbes de niveau. L’une de ces courbes de niveau est un ensemble de valeurs de température et d’entropie le long duquel la pression est constante à \(P\) et \(\theta\) est constante à \({\theta }_1\). L’autre courbe de niveau est un ensemble de valeurs de température et d’entropie le long desquelles la pression est constante à \(P\) et \(\theta\) est constante à \({\theta }_2\). La pente d’une courbe de niveau est
\
Parce que la capacité thermique est toujours positive, cette pente est toujours positive.
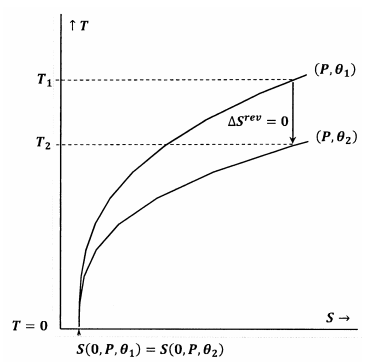
Dans la figure 7, l’énoncé de Lewis et Randall est satisfait. Lorsque la température devient nulle, les lignes de contour se rejoignent à la même valeur de l’entropie ; ces contours satisfont la relation
\
Un chemin adiabatique (vertical) du contour pour \(P\) et \({\theta }_1\) rencontre le contour pour \(P\) et \({\theta }_2\) à une température positive, \(T_2>0\). Puisque ceci est évidemment vrai pour toute \(P\) et toute \({\theta }_2\), l’état final pour tout processus adiabatique aura \(T_2>0\). Comme l’énoncé de Lewis et Randall est satisfait, le système ne peut pas atteindre le zéro absolu, et vice versa.
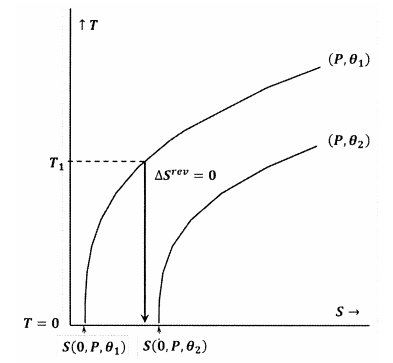
Dans la figure 8, l’énoncé de Lewis et Randall est violé, car nous avons \(S\left(0,P,{\theta }_1\right)\). Dans ce cas, un processus adiabatique initié à partir d’une température initiale suffisamment basse, \(T_1\), atteindra le zéro absolu sans croiser le contour pour les constantes \(P\) et \({\theta }_2\). Comme l’énoncé de Lewis et Randal est violé, le système peut atteindre le zéro absolu, et vice versa.