Utilisez notre service RMN pour les expériences de RMN 2D et autres.
Types de RMN 2D
La spectroscopie RMN à deux dimensions (2D) comprend :-
Homonucléaire
- La liaison traversante : COSY, TOCSY, 2D-INADEQUATE, 2D-ADEQUATE
- Espace traversant : NOESY, ROESY
Corrélation hétéronucléaire
- Corrélation à une liaison HSQC, HMQC
- Corrélation à longue portée HMBC
Exemples d’affectation spectrale 2D
Affectation du 12,14-ditbutylbenzochrysène

Attribution de l’acétate de cholestéryle

La base de la RMN 2D
Dans une expérience de RMN 1D, l’étape d’acquisition des données a lieu juste après la séquence d’impulsions. Cet ordre est maintenu également avec les expériences complexes bien qu’une phase de préparation soit ajoutée avant l’acquisition. Cependant, dans une expérience de RMN 2D, l’étape d’acquisition est séparée de l’étape d’excitation par des étapes intermédiaires appelées évolution et mélange. Le processus d’évolution se poursuit pendant une période de temps appelée t1. L’acquisition des données comprend un grand nombre de spectres qui sont acquis de la manière suivante : la première fois, la valeur de t1 est fixée près de zéro et le premier spectre est acquis. La deuxième fois, t1 est augmenté de Δt et un autre spectre est acquis. Ce processus (d’incrémentation de t1 et d’acquisition de spectres) est répété jusqu’à ce qu’il y ait suffisamment de données pour une analyse utilisant une transformée de Fourier 2D. Le spectre est généralement représenté comme une carte topographique où l’un des axes est f1 c’est-à-dire le spectre dans la dimension t1 et le second axe est celui qui est acquis après les étapes d’évolution et de mélange (similaire à l’acquisition 1D). L’intensité du signal est représentée par une couleur d’autant plus forte qu’il est intense.
Dans la carte topographique résultante, les signaux sont fonction de deux fréquences, f1 et f2. Il est possible qu’un signal apparaisse à une fréquence (par exemple, 20 Hz) en f1 et à une autre fréquence (par exemple, 80 Hz) f2 ; cela signifie que la fréquence du signal a changé pendant le temps d’évolution. Dans une expérience de RMN 2D, on mesure le transfert de magnétisation. Parfois, cela se produit par des liaisons au même type de noyau comme dans COSY, TOCSY et INADEQUATE ou à un autre type de noyau comme dans HSQC et HMBC ou à travers l’espace comme dans NOESY et ROESY.
Les différentes techniques de RMN 2D sont utiles lorsque la RMN 1D est insuffisante comme lorsque les signaux se chevauchent parce que leurs fréquences de résonance sont très similaires. Les techniques de RMN 2D peuvent faire gagner du temps, en particulier lorsqu’on s’intéresse à la connectivité entre différents types de noyaux (par exemple, le proton et le carbone).
L’expérience de RMN 2D de base(fig. 1) consiste en une séquence d’impulsions qui excite les noyaux avec deux impulsions ou groupes d’impulsions puis reçoit la désintégration par induction libre (fid). Les groupes d’impulsions peuvent être purement radiofréquence (rf) ou peuvent inclure des impulsions de gradient magnétique. L’acquisition est effectuée plusieurs fois, en incrémentant le délai (temps d’évolution – t1) entre les deux groupes d’impulsions. Le temps d’évolution est noté t1 et le temps d’acquisition, t2.
Fig. 1. Séquence d’impulsions de base pour une acquisition 2D
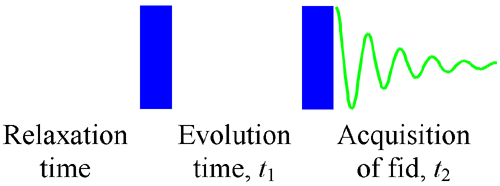
Transformation de Fourier 2D
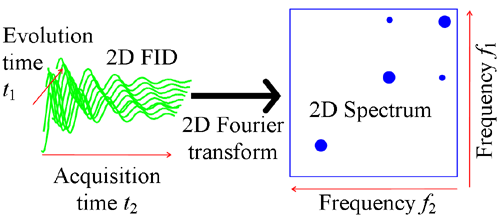
Le FID est ensuite transformé par Fourier dans les deux directions (fig. 2) pour donner le spectre. Le spectre est conventionnellement représenté sous la forme d’un diagramme de contour. La fréquence d’évolution est étiquetée f1 et la fréquence d’acquisition est étiquetée f2 et tracée de droite à gauche.
Fig. 2. Transformée de Fourier 2D
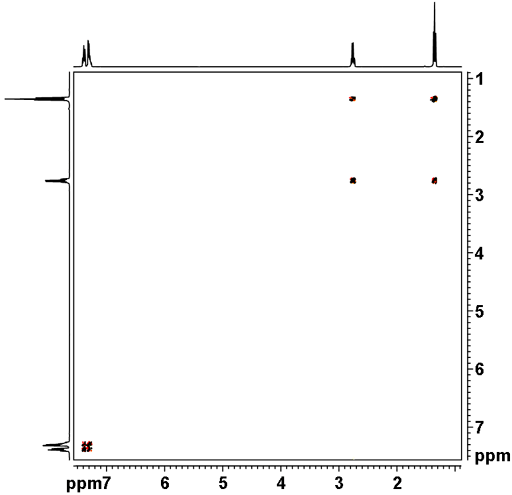
Le spectre 2D est généralement tracé avec ses projections 1D pour plus de clarté. Il peut s’agir de véritables projections ou des spectres 1D équivalents. Dans un spectre homonucléaire, il y a généralement une diagonale (à l’exception de 2D-INADEQUATE) qui représente la corrélation des pics à eux-mêmes et n’est pas en soi très informative. Les signaux éloignés de la diagonale représentent les corrélations entre deux signaux et sont utilisés pour l’attribution. Par exemple, dans le spectre COSY homonucléaire de la figure 3, le signal 1H à 1,4 ppm est corrélé avec le signal 1H à 2,8 ppm car il y a des pics croisés mais ils ne sont pas corrélés avec les signaux à 7.3 ppm.
Fig. 3. Spectre COSY 2D de l’éthylbenzène
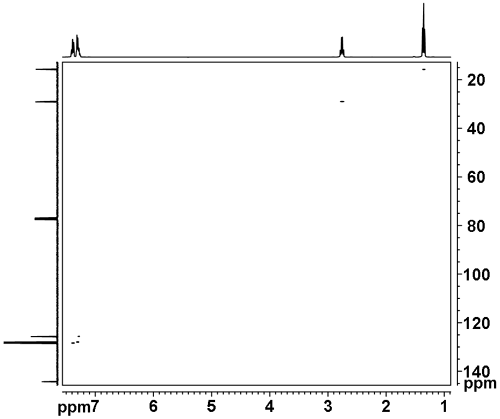
Dans un spectre hétéro-nucléaire, il n’y a pas de signaux diagonaux et tous les signaux représentent des corrélations. Par exemple, dans le spectre de corrélation à courte portée HSQC hétéro-nucléaire de la fig. 4, le signal 1H à 1,4 ppm est corrélé avec le signal 13C à 15,7 ppm, le signal 1H à 2.8 ppm est corrélé avec le signal 13C à 29,0 ppm, etc.
Fig. 4. Spectre HSQC 2D de l’éthylbenzène
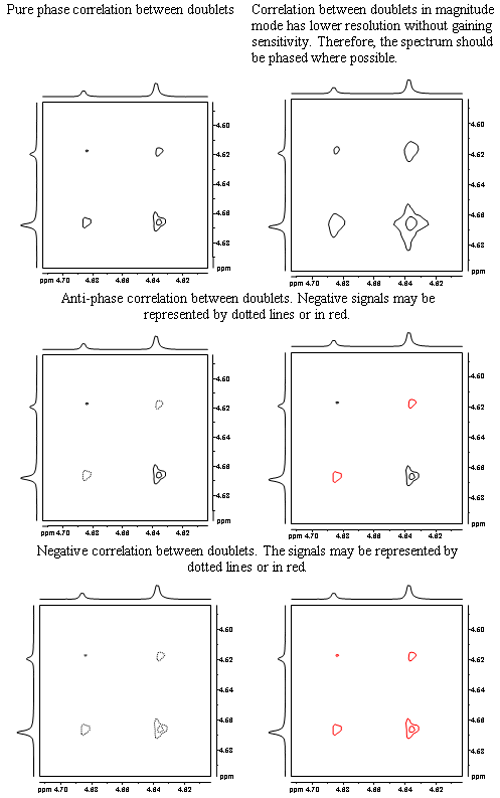
Les signaux dans un spectre 2D ne sont pas toujours en phase pure. Parfois, la phase ne peut pas être exprimée simplement comme dans HMBC et 2D-INADEQUATE, dans ce cas un spectre de magnitude est tracé. Cependant, les spectres de magnitude sacrifient la résolution par rapport aux spectres de phase pure (et contrairement aux fonctions de fenêtre qui élargissent les lignes, ils ne permettent pas de gagner en sensibilité). C’est pourquoi, dans la mesure du possible, le spectre 2D doit être mis en phase. Les signaux résultants peuvent être en phase pure, en opposition de phase ou en phase négative comme dans la figure 5. Les signaux négatifs sont conventionnellement représentés par des contours en pointillés ou en rouge.
Fig. 5. Phases possibles pour une corrélation entre deux doublets
 .
.