Définir la constante d’acidité
Vous savez sans doute que certains acides sont plus forts que d’autres. L’acidité relative de différents composés ou groupes fonctionnels – en d’autres termes, leur capacité relative à donner un proton à une base commune dans des conditions identiques – est quantifiée par un nombre appelé la constante d’acidité, abrégée \(K_a\). La base commune choisie pour la comparaison est l’eau.
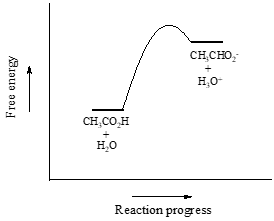
Nous allons considérer l’acide acétique comme notre premier exemple. Si nous faisons une solution diluée d’acide acétique dans l’eau, une réaction acide-base se produit entre l’acide (donneur de protons) et l’eau (accepteur de protons).

L’acide acétique est un acide faible, donc l’équilibre favorise les réactifs par rapport aux produits – il est thermodynamiquement « ascendant ». Ceci est indiqué dans la figure ci-dessus par la longueur relative des flèches de réaction avant et arrière.
La constante d’équilibre \(K_{eq}\) est définie comme:
\}{} = \frac{}{}\]
Rappellez-vous qu’il s’agit d’une solution aqueuse diluée : nous avons ajouté une petite quantité d’acide acétique à une grande quantité d’eau. Par conséquent, au cours de la réaction, la concentration de l’eau (environ 55,6 mol/L) change très peu, et peut être traitée comme une constante.
Si nous déplaçons le terme constant pour la concentration de l’eau vers le côté gauche de l’expression de la constante d’équilibre, nous obtenons l’expression de \(K_a\), la constante d’acide pour l’acide acétique :
\ = \frac{}{}\]
En termes plus généraux, la constante de dissociation pour un acide donné HA ou HB+ s’exprime comme suit :
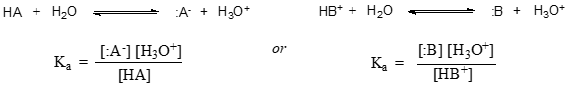
La valeur de \(K_a\) pour l’acide acétique est \(1.75 \times 10^{-5}\) – beaucoup moins que \(1\), ce qui indique qu’il y a beaucoup plus d’acide acétique en solution à l’équilibre que d’acétate et d’ions hydronium.
A l’inverse, l’acide sulfurique, avec un \(K_a\) d’environ \(10^9\), ou l’acide chlorhydrique, avec un \(K_a\) d’environ \(10^7\), subissent tous deux une dissociation essentiellement complète dans l’eau : ce sont des acides très forts.
Un nombre comme \(1,75 \times 10^{- 5}\) n’est pas très facile à dire, à retenir ou à visualiser, c’est pourquoi les chimistes utilisent généralement un terme plus pratique pour exprimer l’acidité relative. La valeur du \(pK_a\) d’un acide est simplement le logarithme (base 10) de sa valeur \(K_a\).
\
En faisant le calcul, nous trouvons que le \(pK_a\) de l’acide acétique est \(4,8\). La valeur du \(pK_a\) de l’acide sulfurique est de -10, et celle de l’acide chlorhydrique de -7. L’utilisation des valeurs du \(pK_a\) nous permet d’exprimer l’acidité relative de composés et de groupes fonctionnels courants sur une échelle numérique allant d’environ -10 (pour un acide très fort) à 50 (pour un composé qui n’est pas du tout acide). Plus la valeur \(pK_a\) est faible, plus l’acide est fort.
Les groupes fonctionnels ionisables (donneurs ou accepteurs de protons) pertinents pour la chimie organique biologique ont généralement des valeurs \(pK_a\) comprises entre environ 5 et environ 20. Les plus importants d’entre eux sont résumés ci-dessous, avec des valeurs de \(pK_a\) très approximatives pour les formes acides conjuguées. Des groupes plus acides avec des valeurs \(pK_a\) proches de zéro sont également inclus pour référence.
Valeurs typiques du \(pK_a\)
| Groupe | Valeur approximative du \(pK_a\) |
|---|---|
| Ion hydronium | 0 |
| alcool protoné | 0 |
| carbonyle protoné | 0 |
| acides carboxyliques | 5 |
| imines protonées | 7 |
| amines protonées. | 10 |
| phénols | 10 |
| thiols | 10 |
| alcools, l’eau | 15 |
| acides carboxyliques * | 20 |
* acides carboxyliques seront expliqués dans la section 7.6A
Il est fortement recommandé de mémoriser ces valeurs approximatives dès maintenant – ensuite, si vous avez besoin d’une valeur plus précise, vous pourrez toujours la rechercher dans un tableau plus complet des \(pK_a\). L’annexe de ce livre contient un tableau plus détaillé des valeurs typiques de \(pK_a\), et des tableaux beaucoup plus complets sont disponibles dans des ressources telles que le Handbook of Chemistry and Physics.
\(pK_a\) vs. \(pH\)
Il est important de réaliser que \(pK_a\) n’est pas la même chose que \(pH\) : le premier est une propriété inhérente à un composé ou à un groupe fonctionnel, tandis que le second est une mesure de la concentration en ions hydronium dans une solution aqueuse donnée :
\\]
Connaître les valeurs de \(pK_a\) nous permet non seulement de comparer la force des acides, mais aussi celle des bases. L’idée clé à retenir est la suivante : plus l’acide conjugué est fort, plus la base conjuguée est faible. Nous pouvons déterminer que l’ion hydroxyde est une base plus forte que l’ammoniac (\(NH_3\)), car l’ion ammonium (\(NH4^+\), \(pK_a = 9.2\)) est un acide plus fort que l’eau (\(pK_a = 15.7\)).
Exercice \(\PageIndex{1}\)
Quelle est la base la plus forte, \(CH_3O^-\) ou \(CH_3S^-\) ? L’ion acétate ou l’ammoniac ? L’ion hydroxyde ou l’ion acétate ?
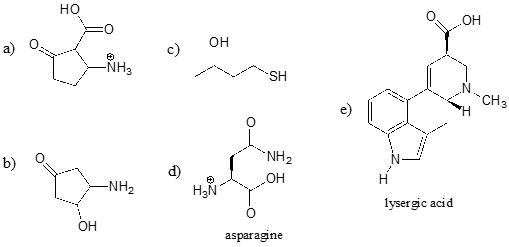
Mettons à profit notre compréhension du concept de \(pK_a\) dans le contexte d’une molécule plus complexe. Par exemple, quelle est l’\(pK_a\) du composé ci-dessous ?

Nous devons évaluer l’acidité potentielle de quatre différents types de protons sur la molécule, et trouver le plus acide. Les protons aromatiques ne sont pas tous acides – leur \(pK_a\) est d’environ 45. Le groupe amine n’est pas non plus acide, son \(pK_a\) est d’environ 35. (Rappelez-vous que les amines non chargées sont basiques : ce sont les amines protonées chargées positivement, avec des valeurs de \(pK_a\) autour de 10, qui sont faiblement acides). Le proton de l’alcool a un \(pK_a\) d’environ 15, et le proton du phénol a un \(pK_a\) d’environ 10 : ainsi, le groupe le plus acide de la molécule ci-dessus est le phénol (assurez-vous de pouvoir reconnaître la différence entre un phénol et un alcool – souvenez-vous que dans un phénol, le groupe \(OH\) est lié directement au cycle aromatique). Si cette molécule devait réagir avec un équivalent molaire d’une base forte comme l’hydroxyde de sodium, c’est le proton du phénol qui serait donné pour former un anion phénolate.
Exercice \(\PageIndex{2}\)
Identifiez le groupe fonctionnel le plus acide sur chacune des molécules ci-dessous, et donnez son \(pK_a\) approximatif.