Calcul de la perte annuelle moyenne
Supposons que vous souhaitiez calculer l’AAL pour un portefeuille de propriétés géographiquement dispersées en utilisant un catalogue d’ouragans sur 10 ans (notez qu’il s’agit d’un exemple inventé à des fins d’illustration uniquement ; les catalogues réels contiennent généralement 10 000, 50 000, voire 100 000 années d’activité simulée). Pour chaque année simulée, il peut y avoir zéro, un ou plusieurs ouragans qui ont un impact sur le portefeuille. L’exécution du modèle par rapport à ce portefeuille dans le logiciel AIR donne les pertes indiquées dans le tableau 1.
| Huragan | |
|---|---|
| Année de simulation | Perte (millions USD) |
| 1 | 25 |
| 2 | 0 |
| 3 | 17 |
| 4 | 34 |
| 5 | 99 |
| 6 | 67 |
| 7 | 0 |
| 8 | 31 |
| 9 | 55 |
| 10 | 29 |
Ces pertes sont ensuite classées pour produire une courbe de probabilité de dépassement et également moyennées pour calculer l’AAL agrégée, comme le montre la figure 1. Dans cet exemple, l’AAD est de 36 millions USD. On remarque que sept années entraînent des pertes inférieures à l’AAD et que trois années entraînent des pertes supérieures. Pendant deux années, aucun ouragan n’a affecté le portefeuille et les pertes ont été nulles.
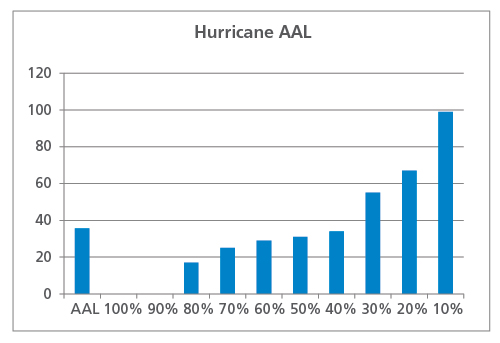
Ce que l’AAD ne révèle pas
Supposons que ce même portefeuille hypothétique de propriétés soit situé près d’une faille sismique dont on s’attend à ce qu’elle se rompe une fois tous les cinq ans. L’exécution d’un catalogue de séismes sur 10 ans contre le portefeuille pourrait donner les pertes indiquées dans le tableau 2.
| Séisme | |
|---|---|
| Année de simulation | Pertes (millions USD) |
| 1 | 0 |
| 2 | 0 |
| 3 | 250 |
| 4 | 0 |
| 5 | 0 |
| 6 | 0 |
| 7 | 0 |
| 8 | 0 |
| 9 | 150 |
| 10 | 0 |
La courbe EP et l’AAL peuvent être calculés comme précédemment, comme le montre la figure 2. L’AAL du tremblement de terre est très similaire à celui de l’ouragan, à 40 millions de dollars, mais il est immédiatement évident que le profil de risque de ces deux périls est très différent.
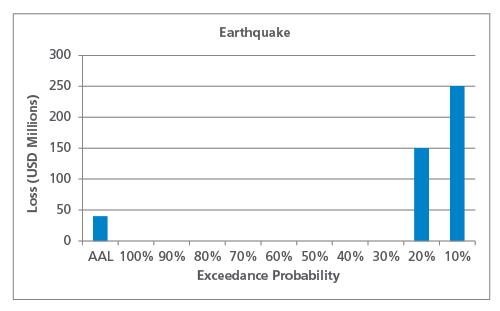
Comme le montre cet exemple simplifié, pour les périls qui se caractérisent par des événements dommageables peu fréquents (comme les tremblements de terre), la queue de la distribution à faible fréquence et à fort impact contribuera davantage à l’AAL que les périls qui présentent une fréquence plus élevée d’événements moins dommageables. Il est important de garder cela à l’esprit lorsque l’on compare l’AAD historique (calculé sur un nombre limité d’années) à l’AAD modélisé. Pour les périls dont l’AAD est piloté par la queue de la distribution, l’AAD historique sera probablement beaucoup plus faible que l’AAD modélisé si un événement de grande ampleur ne s’est pas produit dans la période de temps des données enregistrées.
AAD agrégée et par occurrence
Comme mentionné précédemment, l’AAD peut être déterminée sur une base agrégée ou par occurrence. Tout comme dans la nature, chaque année peut avoir zéro, un ou plusieurs événements dommageables, et l’AAD agrégée prend en considération tous les événements causant des pertes dans chaque année simulée. Les pertes dues à tous les événements sont additionnées, puis divisées par le nombre d’années du catalogue, comme le montrent les exemples de la section précédente.
L’AAL par occurrence, en revanche, se base uniquement sur la plus grande perte de chaque année simulée, de sorte que si deux pertes identiques se produisent au cours de la même année, une seule contribue à l’AAL par occurrence. L’exemple suivant explique le calcul de manière conceptuelle. Notez cependant que l’AAL d’occurrence ne fournit pas une vue très significative du risque ; il est recommandé d’utiliser l’AAL agrégé.
Le tableau 3 montre le même catalogue d’ouragans sur 10 ans, mais cette fois-ci ventilé par événement. La perte la plus importante de chaque année est mise en évidence.
Tableau 3. Catalogue hypothétique d’ouragans sur 10 ans, ventilé par événement
| Huragan | ||
|---|---|---|
| Année de simulation | Numéro de l’événement | Perte (millions USD) |
| 1 | 1 | 25 |
| 2 | 0 | |
| 3 | 2 | 13 |
| 3 | 4 | |
| 4 | 4 | 27 |
| 5 | 7 | |
| 5 | 6 | 16 |
| 7 | 2 | |
| 8 | 49 | |
| 9 | 32 | |
| 6 | 10 | 43 |
| 11 | 11 | |
| 12 | 13 | |
| 7 | 0 | |
| 8 | 13 | 31 |
| 9 | 14 | 55 |
| 10 | 15 | 7 |
| 16 | 22 | |
Only considering the largest loss from each year, la courbe d’occurrence EP et l’occurrence AAL sont présentées dans la figure 3.
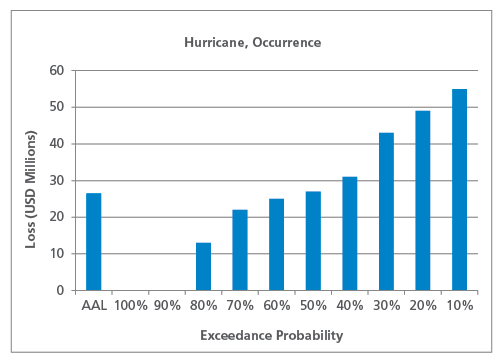
Comme prévu, l’AAL d’occurrence (à 26,5 millions de dollars) est inférieur à l’AAL global. Une fois de plus, la nature du péril affecte la forme de la courbe EP de l’occurrence et la relation entre l’AAL de l’occurrence et l’AAL agrégé. Pour les périls à faible fréquence comme le tremblement de terre, par exemple, il est moins probable que de multiples événements dommageables se produisent la même année, de sorte que l’AAL d’occurrence sera plus proche de l’AAL agrégé que pour les périls à fréquence plus élevée comme l’orage violent.
Pensées finales
Bien que les exemples de cet article aient été beaucoup simplifiés à des fins d’illustration, le point fondamental est que, bien que l’AAL ne soit qu’un seul chiffre et qu’il soit toujours calculé de la même manière, la distribution qui le sous-tend peut avoir une apparence très différente selon le péril, la région et d’autres attributs de danger et de vulnérabilité. Nous explorerons plus en détail le concept de formes de courbes EP et son impact sur l’AAD dans un prochain article, et nous aborderons également certaines questions fréquemment posées et idées fausses sur l’AAD.