Groupe abélien | CDhistory

Un groupe abélien est un groupe pour lequel les éléments commuent (c’est-à-dire pour tous les éléments et ). Les groupes abéliens correspondent donc aux groupes dont les tables de multiplication sont symétriques.

Tous les groupes cycliques sont abéliens, mais un groupe abélien n’est pas nécessairement cyclique. Tous les sous-groupes d’un groupe abélien sont normaux. Dans un groupe abélien, chaque élément est dans une classe de conjugaison par lui-même, et la table de caractères implique des puissances d’un seul élément connu comme générateur de groupe.

Dans le langage Wolfram, la fonction AbelianGroup représente le produit direct des groupes cycliques de degrés , , ….

On ne connaît pas de formule générale pour donner le nombre de groupes finis non isomorphes d’un ordre de groupe donné. Cependant, le nombre de groupes finis abéliens non isomorphes d’un ordre de groupe donné est donné en écrivant comme

(1)

où les sont des facteurs premiers distincts, alors

(2)

où est la fonction de partition, qui est implémentée dans le langage Wolfram comme FiniteAbelianGroupCount. Les valeurs de pour , 2, … sont 1, 1, 1, 2, 1, 1, 1, 3, 2, …. (OEIS A000688).

Les plus petits ordres pour lesquels , 2, 3, … groupes abéliens non isomorphes existent sont 1, 4, 8, 36, 16, 72, 32, 900, 216, 144, 64, 1800, 0, 288, 128, …. (OEIS A046056), où 0 dénote un nombre impossible (c’est-à-dire qui n’est pas un produit de nombres de partition) de groupes abéliens non isomorphes. Les valeurs « manquantes » sont 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41, 43, 46, … (OEIS A046064). Les nombres incrémentaux les plus grands des groupes abéliens en fonction de l’ordre sont 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, … (OEIS A046064). (OEIS A046054), qui apparaissent pour les ordres 1, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, … (OEIS A046055).

Le théorème de décomposition de Kronecker stipule que tout groupe abélien fini peut être écrit comme un produit direct de groupes cycliques d’ordre de groupe de puissance première. Si l’ordre du groupe d’un groupe fini est un nombre premier , alors il existe un seul groupe abélien d’ordre (noté ) et aucun groupe non abélien. Si l’ordre du groupe est un carré premier , alors il existe deux groupes abéliens (notés et . Si l’ordre du groupe est un nombre premier cubique , alors il y a trois groupes abéliens (notés , , et ), et cinq groupes au total. Si l’ordre est un produit de deux nombres premiers et , alors il existe exactement un groupe abélien d’ordre (noté ).

Un autre résultat intéressant est que si désigne le nombre de groupes abéliens non isomorphes d’ordre , alors

(3)

où est la fonction zêta de Riemann.

Les nombres de groupes abéliens d’ordres sont donnés par 1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15, 17, 18, 19, 20, 25, …. (OEIS A063966) pour , 2, …. Srinivasan (1973) a également montré que

(4)

où

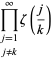			(5)
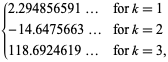			(6)

(OEIS A021002, A084892, et A084893) et est encore la fonction zêta de Riemann. Notez que Richert (1952) a donné incorrectement . Les sommes peuvent aussi être écrites sous les formes explicites