Intervalles de tolérance
Cette section contient des détails statistiques pour les intervalles de tolérance unilatéraux et bilatéraux.
Intervalles basés sur la distribution normale
Intervalle unilatéral
L’intervalle unilatéral est calculé comme suit :
La limite inférieure = 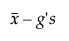
La limite supérieure = 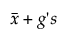
où
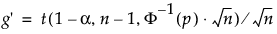
s est l’écart type
t est le quantile de la distribution t noncentral t-distribution
Φ-1 est le quantile normal standard
Intervalle bilatéral
L’intervalle bilatéral est calculé comme suit :
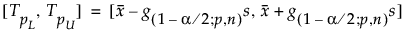
où s est l’écart-type et g(1-α/2 ; p,n) est une constante.
Pour déterminer g, on considère la fraction de la population capturée par l’intervalle de tolérance. Tamhane et Dunlop (2000) donnent cette fraction comme suit :
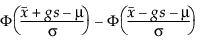
où Φ désigne la cdf (fonction de distribution cumulative) normale standard.
Donc, g résout l’équation suivante :
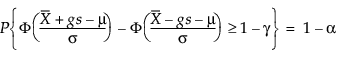
où 1 – γ est la fraction de toutes les observations futures contenues dans l’intervalle de tolérance.
Pour plus d’informations sur les intervalles de tolérance basés sur la distribution normale, voir les tableaux J.1.a, J.1b, J.6a, et J.6b de Meeker et al. (2017).
Intervalles non paramétriques
Limite inférieure unilatérale
La limite de tolérance unilatérale inférieure de 100(1 – α)% pour contenir au moins une proportion β de la distribution échantillonnée à partir d’un échantillon de taille n est la statistique d’ordre x(l). L’indice l est calculé comme suit :
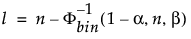
où Φ-1bin(1-α, n, β) est le (1 – α)ème quantile de la distribution binomiale avec n essais et une probabilité de succès β.
Le niveau de confiance réel est calculé comme Φbin(n-l, n, β), où Φbin(x, n, β) est la probabilité qu’une variable aléatoire distribuée de façon binomiale avec n essais et une probabilité de succès β soit inférieure ou égale à x.
Notez que pour calculer un intervalle de tolérance inférieur unilatéral sans distribution, la taille de l’échantillon n doit être au moins aussi grande que 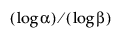 .
.
Limite supérieure unilatérale
La limite supérieure de tolérance unilatérale de 100(1 – α)% pour contenir au moins une proportion β de la distribution échantillonnée à partir d’un échantillon de taille n est la statistique d’ordre x(u). L’indice u est calculé comme suit :
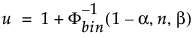
où Φ-1bin(1-α, n, β) est le (1 – α)ème quantile de la distribution binomiale avec n essais et une probabilité de succès β.
Le niveau de confiance réel est calculé comme Φbin(u-1, n, β), où Φbin(x, n, β) est la probabilité qu’une variable aléatoire distribuée de façon binomiale avec n essais et une probabilité de succès β soit inférieure ou égale à x.
Notez que pour calculer un intervalle de tolérance supérieur unilatéral sans distribution, la taille de l’échantillon n doit être au moins aussi grande que 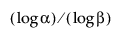 .
.
Intervalle bilatéral
L’intervalle de tolérance bilatéral de 100(1 – α)% pour contenir au moins une proportion β de la distribution échantillonnée à partir d’un échantillon de taille n est calculé comme suit :
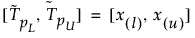
où x(i) est la statistique du ième ordre et l et u sont calculés comme suit :
Let ν = n – Φ-1bin(1-α, n, β), où Φ-1bin(1-α, n, β) est le (1 – α)ième quantile de la distribution binomiale avec n essais et une probabilité de succès β. Si ν est inférieur à 2, un intervalle de tolérance sans distribution bilatérale ne peut pas être calculé. Si ν est supérieur ou égal à 2, l = plancher(ν/2) et u = plancher(n + 1 – ν/2).
Le niveau de confiance réel est calculé comme Φbin(u-l-1, n, β), où Φbin(x, n, β) est la probabilité qu’une variable aléatoire distribuée de façon binomiale avec n essais et une probabilité de succès β soit inférieure ou égale à x.
Notez que pour calculer un intervalle de tolérance bilatéral sans distribution, la taille de l’échantillon n doit être au moins aussi grande que le n de l’équation suivante :

Pour plus d’informations sur les intervalles de tolérance sans distribution, voir Meeker et al. (2017, sec. 5.3).