Nous avons commencé par les convolutions 2D dans le premier post parce que les convolutions ont gagné une popularité significative après les succès dans le domaine de la vision par ordinateur. Comme les tâches dans ce domaine utilisent des images comme entrées, et que les images naturelles ont généralement des motifs le long de deux dimensions spatiales (de hauteur et de largeur), il est plus courant de voir des exemples de convolutions 2D que de convolutions 1D et 3D.
Plus récemment cependant, il y a eu un nombre énorme de succès dans l’application des convolutions aux tâches de traitement du langage naturel aussi. Puisque les tâches dans ce domaine utilisent du texte comme entrées, et que le texte a des motifs le long d’une seule dimension spatiale (c’est-à-dire le temps), les convolutions 1D conviennent parfaitement ! Nous pouvons les utiliser comme des alternatives plus efficaces aux réseaux neuronaux récurrents (RNN) traditionnels tels que les LSTM et les GRU. Contrairement aux RNN, ils peuvent être exécutés en parallèle pour des calculs vraiment rapides.
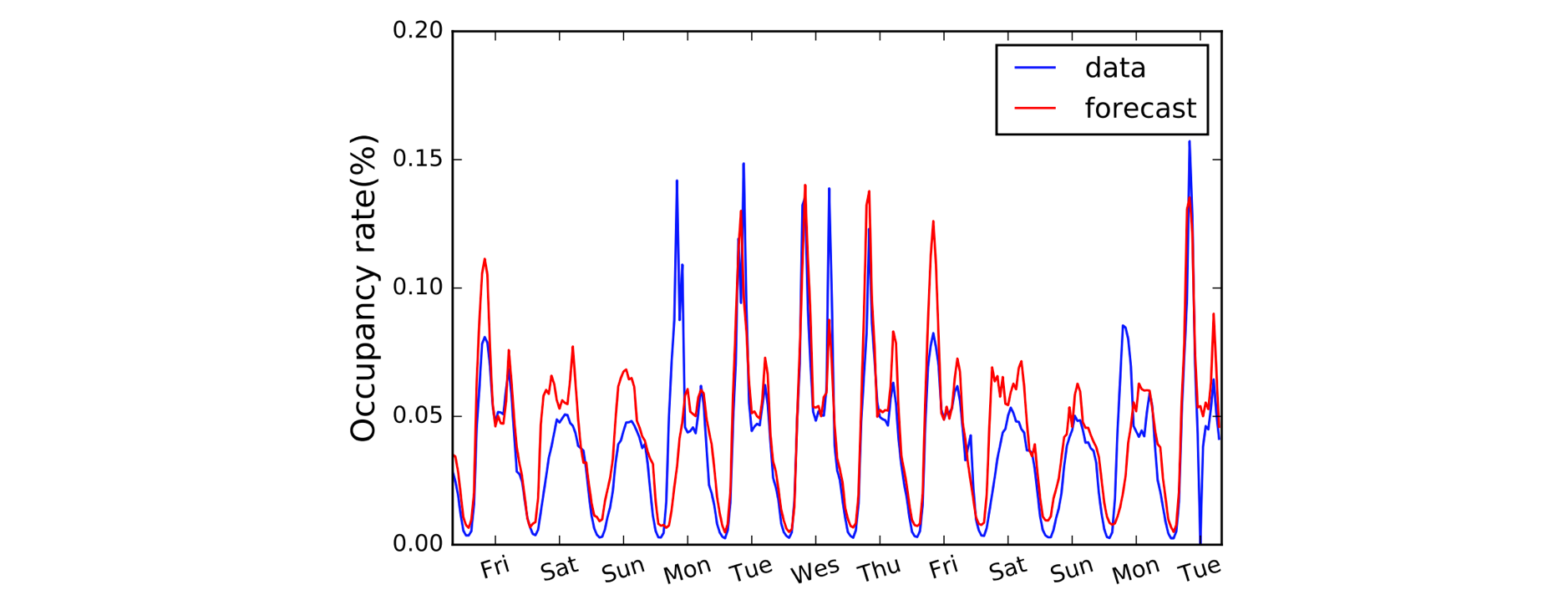
Un autre domaine qui bénéficie des convolutions 1D est la modélisation des séries temporelles. Comme précédemment, nous avons une seule dimension spatiale sur nos données d’entrée (c’est-à-dire le temps), et nous voulons capter des modèles sur des périodes de temps. Nous appelons souvent ce type de données « séquentielles » car elles peuvent être considérées comme une séquence de valeurs. Et la dimension spatiale est souvent appelée dimension « temporelle ». L’utilisation de convolutions 1D avant les RNN est également assez courante : le modèle LSTNet en est un exemple et ses prédictions pour la prévision du trafic sont présentées ci-dessous.
A, B, C. C’est facile comme (1,3,3) point (2,0,1) = 5.
Avec les conventions de dénomination clarifiées, regardons maintenant de plus près l’arithmétique. Nous avons de la chance car les convolutions 1D ne sont en fait qu’une version simplifiée de la convolution 2D !

En travaillant sur le calcul d’une seule valeur de sortie, nous pouvons appliquer notre noyau de taille 3 à la région de taille équivalente sur le côté gauche de notre matrice d’entrée. Nous calculons le « produit scalaire » de la région d’entrée et du noyau, qui, pour récapituler, est juste le produit élément par élément (c’est-à-dire multiplier les paires de couleurs) suivi d’une somme globale pour obtenir une valeur unique. Donc dans ce cas :
(1*2) + (3*0) + (3*1) = 5
Nous appliquons la même opération (avec le même noyau) aux autres régions du tableau d’entrée pour obtenir le tableau de sortie complet de (5,6,7,2) ; c’est-à-dire que nous faisons glisser le noyau sur l’ensemble du tableau d’entrée. Contrairement aux convolutions 2D, où nous faisons glisser le noyau dans deux directions, pour les convolutions 1D, nous ne faisons glisser le noyau que dans une seule direction ; gauche/droite dans ce diagramme.
Avancé : une convolution 1D n’est pas la même qu’une convolution 2D 1×1.
Codage des choses en haut
Sans surprise, nous aurons besoin d’un Conv1Dbloc dans Gluon pour notre convolution 1D. Nous définissons la forme du noyau comme 3, et puisque nous ne travaillons qu’avec un seul noyau dans cet exemple, nous allons spécifier channels=1.
import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)
Nous pouvons maintenant passer notre entrée dans le bloc conv en utilisant un noyau prédéfini.
input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>
Qu’est-ce qui change avec le padding, le stride et la dilatation ?
Nous avons vu l’effet du padding, du stride et de la dilatation dans le dernier post sur les Convolutions 2D, et c’est très similaire pour les Convolutions 1D. Avec le padding, nous ne paddons que le long d’une seule dimension (la dimension temporelle) cette fois. Notre diagramme représente le temps sur l’axe horizontal, nous remplissons donc à gauche et à droite des données d’entrée (et non au-dessus et en dessous comme dans l’exemple de la convolution 2D). Pour ce qui est de l’enjambement et de la dilatation, nous les appliquons également uniquement le long de la dimension temporelle. Ainsi, un exemple avec padding et stride ressemblerait à ceci:

Nous ajoutons deux arguments supplémentaires dans le code : padding=1 et strides=2.
conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>
Avancé : les dimensions des données d’entrée doivent se conformer à un ordre particulier appelé la disposition. Par défaut, la convolution 1D s’attend à être appliquée à des données d’entrée du format ‘NCW’, c’est-à-dire taille du lot (N) * canaux (C) * largeur/temps (W). Et pour les convolutions 2D, le défaut est NCHW, c’est-à-dire taille du lot (N) * canaux (C) * hauteur (H) * largeur (W). Consultez l’argument
layoutdeConv1DetConv2D.
.