Reconstruction 3D

Dans cette pratique, l’intention est de programmer la logique nécessaire pour permettre au robot kobuki de générer une reconstruction 3D de la scène qu’il reçoit à travers ses caméras gauche et droite.

Installation

Installer l’infrastructure générale de l’Académie de robotique JdeRobot.

Comment faire fonctionner votre solution ?

Naviguer dans le répertoire 3d_reconstruction

cd exercises/3d_reconstruction

Lancer Gazebo avec le monde kobuki_3d_reconstruction par la commande

roslaunch ./launch/3d_reconstruction_ros.launch

Puis il faut exécuter l’application académique, qui va intégrer votre code :

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

Comment réaliser l’exercice ?

Pour réaliser l’exercice, vous devez éditer le fichier MyAlgorithm.py et y insérer votre code, qui reconstruit des points 3d à partir des deux vues stéréo.

Où insérer le code ?

Dans le fichier MyAlgorithm.py,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Interface de programmation applicative

• self.getImage('left') – pour obtenir l’image gauche
• self.getImage('right') – pour obtenir l’image droite
• self.point.PlotPoint(position, color) – pour tracer le point dans l’outil 3d

Navigation dans l’interface graphique

Fondée sur la souris : Maintenir et glisser pour se déplacer dans l’environnement. Faites défiler pour faire un zoom avant ou arrière

Sur le clavier : Touches fléchées pour se déplacer dans l’environnement. Touches W et S pour faire un zoom avant ou arrière

Théorie

En vision par ordinateur et en infographie, la reconstruction 3D est le processus de détermination du profil 3D d’un objet, ainsi que la connaissance de la coordonnée 3D de tout point sur le profil. La reconstruction peut être réalisée comme suit :

• Basée sur le matériel : L’approche basée sur le matériel nous oblige à utiliser le matériel spécifique à la tâche de reconstruction. L’utilisation de la lumière structurée, du télémètre laser, de la jauge de profondeur et des méthodes radiométriques sont quelques exemples.

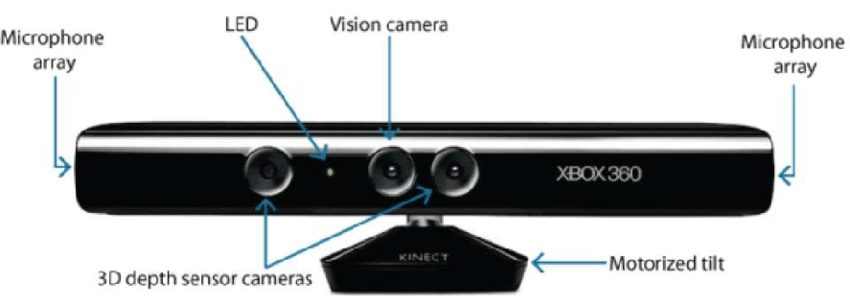
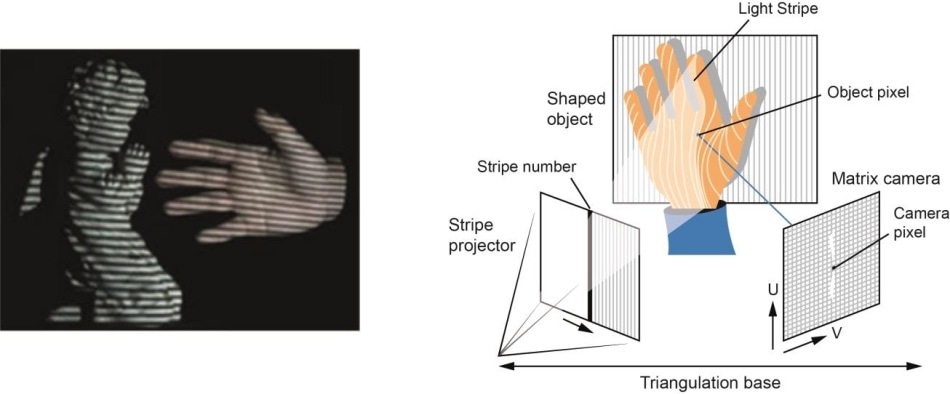
• Software Based : L’approche basée sur le logiciel s’appuie sur les capacités de calcul de l’ordinateur pour déterminer les propriétés 3D de l’objet. La forme à partir de l’ombrage, de la texture, de la vision stéréo et de l’homographie sont quelques bonnes méthodes.

Dans cet exercice, notre objectif principal est de réaliser une reconstruction 3d à l’aide d’une approche basée sur le logiciel, en particulier la reconstruction 3d par vision stéréo.

Géométrie épipolaire

Lorsque deux caméras visualisent une scène 3D depuis deux positions différentes, il existe un certain nombre de relations géométriques entre les points 3D et leurs projections sur les images 2D qui conduisent à des contraintes entre les points de l’image. L’étude de ces propriétés et contraintes est appelée géométries épipolaires. L’image et l’explication ci-dessous peuvent généraliser l’idée:

Supposons qu’un point X dans l’espace 3d soit imagé dans deux vues, à x dans la première et x' dans la seconde. En rétroprojetant les rayons vers leur centre de caméra à travers les plans d’image, on obtient une surface plane, notée π.

Supposant maintenant que nous ne connaissons que x, nous pouvons nous demander comment le point correspondant x' est contraint. Le plan π est déterminé par la ligne de base(ligne reliant les centres des caméras) et le rayon défini par x. D’après ce qui précède, nous savons que le rayon correspondant au point inconnu x' se trouve dans π, donc le point x' se trouve sur la ligne d’intersection l' de π avec le deuxième plan image. Cette ligne est appelée la ligne épipolaire correspondant à x. Cette relation nous aide à réduire l’espace de recherche du point dans l’image de droite, d’un plan à une ligne. Voici quelques définitions importantes à noter :

• L’épipole est le point d’intersection de la ligne joignant les centres des caméras (la ligne de base) avec le plan image.

• Un plan épipolaire est un plan contenant la ligne de base.

• Une ligne épipolaire est l’intersection du plan épipolaire avec le plan image.

Reconstruction stéréo

La reconstruction stéréo est un cas particulier de la reconstruction 3d ci-dessus où les deux plans image sont parallèles entre eux et à égale distance du point 3d que l’on veut tracer.

Dans ce cas, la ligne épipolaire pour les deux plans images sont les mêmes, et sont parallèles à la largeur des plans, simplifiant mieux notre contrainte.

Algorithme de reconstruction 3D

L’algorithme de reconstruction se compose de 3 étapes :

1. Détecter les points caractéristiques dans un plan de l’image
2. Détecter le point caractéristique correspondant à celui trouvé ci-dessus
3. Trianguler le point dans l’espace 3d

Regardons-les un par un

Détection de points caractéristiques

La détection de points caractéristiques est un vaste domaine d’étude où plusieurs algorithmes sont déjà étudiés. Les algorithmes Harris Corner Detection et Shi-Tomasi utilisent les valeurs propres pour obtenir un bon point caractéristique. Mais, le problème est que nous avons besoin de beaucoup de points pour la Reconstruction 3D, et ces algorithmes ne pourront pas nous fournir un si grand nombre de points caractéristiques.

Par conséquent, nous utilisons les points de bord comme points caractéristiques. Il peut y avoir une ambiguïté dans leur détection dans l’étape suivante de l’algorithme. Mais, notre problème est résolu en prenant les bords comme points caractéristiques. L’algorithme de détection des bords de Canny est un détecteur de bords très efficace. Cet algorithme est assez simple et fiable en termes de génération des bords.

Extraction des points de caractéristiques

L’utilisation de la contrainte épipolaire simplifie vraiment la complexité temporelle de notre algorithme. Pour les problèmes généraux de reconstruction 3d, nous devons générer une ligne épipolaire pour chaque point d’une image, puis rechercher dans cet espace échantillon le point correspondant dans l’autre image. La génération de la ligne épipolaire est également très facile dans notre cas, c’est juste l’iterpolation de la ligne parallèle de l’image gauche au plan de l’image droite.

La vérification de la correspondance entre les images implique de nombreux algorithmes, comme la somme des différences au carré ou la minimisation de l’énergie. Sans aller beaucoup plus en profondeur, l’utilisation d’un simple filtre de corrélation suffit également à notre cas d’utilisation.

Triangulation

La triangulation en termes simples est juste le calcul de l’endroit où le point 3d va se trouver en utilisant les deux points déterminés dans les plans d’image.

En réalité, la position des points d’image ne peut pas être mesurée exactement. Pour les caméras générales, il peut y avoir des distorsions géométriques ou physiques. Par conséquent, beaucoup de mathématiques vont derrière la minimisation de cette erreur et le calcul de la projection de points 3d la plus précise. Référez-vous à ce lien pour un modèle simple.

Hints

Des conseils simples fournis pour vous aider à résoudre l’exercice 3d_reconstruction. La bibliothèque OpenCV est largement utilisée pour cet exercice.

Setup

En utilisant l’API de l’exercice, nous pouvons facilement récupérer les images. De plus, après avoir obtenu les images, c’est une bonne idée d’effectuer un filtrage bilatéral sur les images, car il y a quelques détails supplémentaires qui ne doivent pas être inclus pendant la reconstruction 3d. Consultez les illustrations pour les effets de l’exécution du filtrage bilatéral.

Calcul des correspondances

OpenCV a déjà des filtres de corrélation intégrés qui peuvent être appelés par matchTemplate(). Faites attention aux cas extrêmes comme les bords et les coins.

Une bonne observation est que les points à gauche auront une correspondance dans la partie gauche et les points à droite auront une correspondance dans la partie droite. En utilisant cette observation, nous pouvons facilement accélérer le calcul de la correspondance.

Tracer les points

La fonction manuelle ou basée sur OpenCV triangulatePoints fonctionne bien pour la triangulation. Il suffit de prendre soin de toutes les formes et tailles de matrice tout en effectuant les implémentations algébriques.

Gardez à l’esprit la différence entre les coordonnées 3D simples et les coordonnées 4D homogènes. Consultez cette vidéo pour plus de détails. En divisant simplement le vecteur 4d complet par sa 4e coordonnée, on obtient les coordonnées 3d.

En raison des implémentations variées des utilisateurs, l’utilisateur peut avoir à ajuster l’échelle et le décalage des points triangulés afin de les rendre visibles et représentables dans l’interface graphique. La réduction de l’échelle du vecteur de coordonnées 3D par une valeur comprise entre 500 et 1000 fonctionne bien. De même, un décalage de 0 à 8 fonctionne bien.

Illustrations

.