Regardez les articles récents

Abstract

La lumière se déplace dans le vide à la vitesse c indépendamment du mouvement de la source de lumière ou de celui du cadre de référence d’un observateur. Par conséquent, un certain temps est nécessaire pour que la lumière se déplace d’une source de lumière à un observateur dans l’espace, de sorte que l’émission de lumière et l’observation de la lumière émise ne sont pas simultanées. Sur la base de ces considérations, une méthode de mesure de la vitesse absolue d’un observateur est proposée, qui pourrait être utilisée pour déterminer l’état de mouvement d’un vaisseau spatial depuis l’intérieur d’une cabine fermée. Dans cette étude, une nouvelle explication de la transformation de Lorentz est également introduite.

Mots clés

système de coordonnées, système de référence, mouvement, vitesse absolue, relativité, transformation de lorentz, temps, espace, observateur, source lumineuse
L’analyse suivante présente une approche pratique pour mesurer la vitesse absolue d’un observateur, qui pourrait être utilisée pour déterminer l’état de mouvement d’un vaisseau spatial depuis l’intérieur d’une cabine fermée. Le concept de vitesse absolue fait généralement référence à une vitesse uniforme standard des différents objets d’un système physique par rapport à un espace immobile postulé qui existe indépendamment des objets physiques qu’il contient (c’est-à-dire un espace absolu). Nous présentons ici une approche basée sur la cinématique rigide pour démontrer que la vitesse absolue d’un observateur peut être déterminée à partir du fait que la lumière voyage dans le vide à la vitesse c, indépendamment du mouvement de la source lumineuse ou de celui du cadre de référence de l’observateur. Par conséquent, un certain temps est nécessaire pour que la lumière voyage d’une source de lumière à un observateur dans l’espace, de sorte que l’émission de lumière et l’observation de la lumière émise ne sont pas simultanées.
Dans l’analyse proposée, nous fournissons d’abord les conventions suivantes pour les systèmes de coordonnées considérés. Nous supposons un système de coordonnées cartésiennes composé de trois axes perpendiculaires par paire ayant pour origine le point (0,0,0), où tout point P dans l’espace peut être défini par ses coordonnées le long des axes x, y et z, représentées par une paire ordonnée de nombres réels (x,y,z). On suppose qu’un système de référence inertiel S est représenté par un système de coordonnées spatiales rectangulaires (x, y, z) dont l’origine est O. Une série d’horloges standard (appelées horloges S) sont situées en des points fixes de S. Les horloges S sont mutuellement étalonnées (c’est-à-dire qu’elles fournissent des lectures équivalentes au même instant) sur la base de la transmission et de la réception d’un signal lumineux. Plus précisément, au moment tA, un faisceau lumineux est projeté de l’horloge A vers l’horloge B, qui est ensuite réfléchi au moment tB par l’horloge B vers l’horloge A, et arrive à l’horloge A au moment tA’. Si , les deux horloges sont étalonnées. Pour tout événement situé aux coordonnées x,y,z, sa coordonnée temporelle t est donnée par la lecture de l’horloge S liée à l’événement. De même, un autre système de référence inertiel S’ est établi sur la base d’un second système de coordonnées rectangulaires spatiales (x’,y’,z’) dont l’origine est O’, et une autre série d’horloges standard mutuellement étalonnées (horloges S’) sont situées en des points fixes du système de référence S’. Pour tout événement situé aux coordonnées x’, y’, z’, sa coordonnée temporelle t’ est donnée par la lecture de l’horloge S’ liée à l’événement.
Parce que les origines respectives des coordonnées spatiales et temporelles, ainsi que les directions des axes de coordonnées peuvent être choisies arbitrairement dans une large mesure, les relations entre S et S’ employées ici sont basées sur les conventions suivantes, qui ont été appliquées par souci de simplicité.
(1) A un instant donné, les origines et les axes de coordonnées des deux systèmes sont superposés, et les horloges situées respectivement à O et O’ sont mises à zéro, c’est-à-dire , .
(2) Les axes x et x’ coïncident dans la direction du mouvement relatif de S et S’ ; ainsi, x et x’ coïncident à tout moment, tandis que y et y’, ainsi que z et z’ sont parallèles.
(3) S’ se déplace dans la direction +x de S.
L’analyse proposée repose sur le principe fondamental selon lequel la lumière dans le vide se déplace à une vitesse constante c indépendamment du mouvement de l’observateur ou de la source lumineuse. Ainsi, nous définissons ici la vitesse absolue U de l’observateur, qui est supposée être linéaire et uniforme, comme , où f(φ) représente une fonction de la relation géométrique entre la direction d’un signal lumineux et la direction de U, désignée ici par φ.
Deux nouvelles explications de la relativité du temps et de la longueur sont fournies dans l’analyse proposée, qui diffèrent des explications d’Einstein (veuillez vous référer à « Sur l’électrodynamique des corps en mouvement »). Ces explications sont introduites dans les sections suivantes.

La relativité du temps

En raison de la vitesse finie de la lumière, un certain temps est nécessaire pour que la lumière voyage d’une source de lumière à un observateur dans l’espace. On peut donc en déduire que l’émission de la lumière et l’observation de la lumière ne peuvent être simultanées. Sur la base de la constance de la vitesse de la lumière et des conditions illustrées dans la figure 1, nous définissons les facteurs suivants. Les positions d’une source de lumière et d’un observateur à , moment où la source de lumière émet de la lumière (noté événement R), sont données respectivement comme A et H0. Pendant la période de propagation de la lumière de à , l’observateur parcourt une distance U∙T de la position H0 à H, après quoi il reçoit la lumière émise. En conséquence, nous définissons comme la distance l entre la position de l’observateur lors de la réception du signal lumineux en et la position de la source lumineuse lors de l’émission de la lumière en . En raison de la constance de la vitesse de la lumière, . La distance est équivalente à U∙T. Enfin, nous définissons comme la distance l0 entre la position de l’observateur à et la position de la source lumineuse à . Nous introduisons ici une considération de la position de l’observateur en , dont on pensait auparavant qu’elle n’avait aucune signification physique. Si les états de mouvement de l’observateur et de la source lumineuse sont équivalents, l0 est donné, de sorte que U peut être calculé via les relations triangulaires illustrées dans la figure 1.
Dans le présent travail, le temps d’un événement est mesuré en utilisant la méthode suivante. L’observateur et une horloge sont placés à l’origine. Lorsque le signal lumineux représentant l’occurrence d’un événement atteint l’observateur, l’heure d’arrivée de la lumière correspondra à l’heure indiquée par l’horloge. L’avantage de cette correspondance est qu’elle est toujours liée à la position de l’observateur qui emploie l’horloge. Comme on peut le voir sur la figure 1, le point spatial O3 peut être défini en fonction de la position de la source lumineuse lorsqu’elle émet de la lumière à , et le point spatial O2 peut être défini en fonction de la position de l’observateur lorsqu’il reçoit de la lumière à . Cependant, le moyen de définir le point spatial O1 auquel se trouve l’observateur lorsque la source lumineuse émet de la lumière à n’est pas évident. Pour résoudre ce problème, on introduit les concepts de repos absolu (c’est-à-dire ) et de mouvement absolu (c’est-à-dire ). On remplace respectivement l’observateur unique en mouvement à H0 et H par deux observateurs H1 et H2 au repos aux points spatiaux O1 et O2, respectivement, tandis que la source lumineuse A est au repos au point spatial O3. Chacun des observateurs et la source lumineuse utilisent des horloges étalonnées, et A émet un signal lumineux à , appelé événement R0. Lorsque l’observateur H1 reçoit le signal lumineux se déplaçant à c, la lecture de l’horloge est T0, et lorsque H2 le reçoit, la lecture est T. Ainsi, les distances et peuvent être définies sur la base des temps de parcours respectifs du signal lumineux comme suit :
, (1)
et
. (2)
Selon les relations triangulaires présentées sur la figure 1, la transformation de l’événement R0 entre les observateurs H1 et H2 est donnée comme suit :
(3)
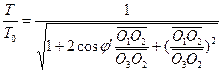(4)
Ici, est l’angle entre la ligne O3O1 et l’axe x, et est l’angle entre la ligne O3O2 et l’axe x.
Retournons maintenant à la condition d’un seul observateur en mouvement, nous supposons que, dans le système S, l’observateur H et la source lumineuse A emploient tous deux une horloge standard étalonnée. A l’instant de l’événement R, la source lumineuse A est au point spatial O3, et l’observateur H est à O1. L’instant où le signal lumineux atteint le point spatial O1 correspond à une lecture de l’horloge S de T0. Lorsque l’observateur H reçoit le signal lumineux, la lecture est T, et H est à O2.
Bien sûr, H ne peut pas observer l’événement R au point O1. Pour résoudre ce problème, un autre observateur H- est placé dans le système S au point O1 correspondant à , où la position de H- est employée pour définir le point spatial O1. Ensuite, la transformation de l’événement R entre les observateurs H- et H peut être obtenue par l’équation (3) comme suit.
(5)
Hence, les équations (3) et (4) peuvent être réécrites comme suit.
(6)
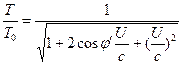(7)
On observe également que, pour , les équations (6) et (7) se simplifient comme suit .
(8)
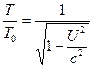(9)
Donc, sur la base de l’analyse ci-dessus, une méthode simple pour déterminer U peut être obtenue à partir de l’équation (6), étant donné que (φ) est connu.
Pour des raisons de simplicité, on choisit comme cadre de référence une source lumineuse dont l’état de mouvement est équivalent à celui des observateurs. Un observateur est placé au centre d’une barre rigide droite en mouvement linéaire uniforme, et les signaux lumineux provenant de différentes positions sur la barre arrivent à l’observateur à des moments différents. L’observateur détecte la déviation de la barre à la position de l’observateur avec un angle de déviation qui peut être obtenu à partir de l’équation (8).
A travers cette méthode, l’état de mouvement d’un vaisseau spatial pourrait être déterminé à partir d’une cabine fermée.

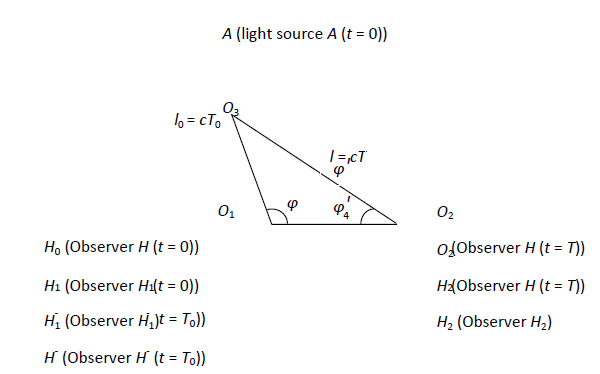
Figure 1 : états de mouvement de l’observateur et de la source lumineuse

La relativité de la longueur

Dans l’analyse ci-dessus, deux longueurs ont été introduites, à savoir et . Dans ce cas, on considère la longueur d’une barre que l’on suppose être une barre rigide stationnaire de longueur L dans son système de coordonnées, pour laquelle L est mesurée avec une jauge d’état-major stationnaire, et où l’axe de la barre coïncide avec l’axe x d’un système de coordonnées qui se déplace avec un mouvement linéaire uniforme le long de la direction +x à une vitesse absolue U. On suppose que L est déterminée par les deux opérations définies ci-dessous.
(a) L’observateur réside dans le même système de coordonnées mobiles que la barre et la jauge de la mire, et L est mesurée par superposition de la barre et de la jauge de la mire.
(b) A l’aide de plusieurs horloges positionnées en coordonnées fixes, qui se déplacent de manière synchronisée, l’observateur mesure les positions des deux extrémités de la barre en coordonnées fixes à un instant précis t, et la distance entre les deux positions est mesurée avec la jauge de la mire fixe. est la longueur calculée à partir de l’opération (a), qui est désignée ici comme la longueur de la barre dans les coordonnées mobiles. est la longueur calculée à partir de l’opération (b), qui est désignée ici comme la longueur d’une barre mobile dans la coordonnée stationnaire. Il est évident que et sont différents.
Nous supposons que, dans le système S, l’observateur H- est dans le même état de mouvement que H. Alors, comme le montre la figure 1, H- est au point O1 lorsqu’il reçoit le signal lumineux à , et, simultanément, l’observateur H est au point O4. Par conséquent, t=0,04
est la distance entre H- et H à , et
. (10)
est la distance parcourue par l’observateur H dans l’intervalle de T0 à T, telle que
. (11)
est la distance entre H- à et H à , telle que
. (12)
Comme tel, on peut déduire l’expression suivante.
(13)
Puis, nous allons considérer les transformations de coordonnées et de temps entre deux systèmes de coordonnées mobiles, qui se déplacent tous deux avec une vitesse linéaire uniforme, ce qui représente une nouvelle explication de la transformation de Lorentz.
Supposons que l’observateur H (dans le système S), l’observateur H’ (dans le système S’), et la source lumineuse A » (dans le système S ») emploient tous individuellement des horloges étalons calibrées, et, à , la source lumineuse A » émet un signal lumineux, noté événement R ». A l’instant de l’événement R », A » est au point O3, et les observateurs H et H’ coïncident. Lorsque l’observateur H reçoit le signal lumineux, la lecture de l’horloge S est T, et H est au point O1. Lorsque l’observateur H’ reçoit le signal lumineux, la lecture de l’horloge S’ est T’, et H’ est au point O2. Alors, la transformation de l’événement R » entre les observateurs H’ et H peut être calculée à partir de l’équation (3), où
. (14)
Ici, u est la vitesse relative entre les observateurs H’ et H, ce qui donne les transformations suivantes.
(15)
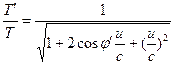(16)
De , on peut déduire les relations suivantes :
. (17)
Lorsque et , l’équation (16) se simplifie en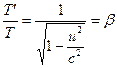
. (18)
On peut donc en déduire les relations de transformation suivantes :
, (19)
, (20)
, (21)
. (22)
En outre, lorsque ,
, (23)
et
, (24)
, (25)
, (26)
. (27)