La procédure de soustraction pour l’élimination de la PL a été élaborée pour la première fois il y a environ deux décennies . Cette procédure n’affecte pas les composantes de l’ECG voisines de la fréquence PL. Cette étude théorique est réalisée pour la fréquence PL de base, mais les conclusions sont également valables pour ses harmoniques et, par conséquent, pour une forme d’onde d’interférence arbitraire. L’efficacité de la procédure ne dépend pas de l’amplitude de l’interférence, tant que l’amplificateur n’est pas saturé. En outre, la procédure s’adapte avec succès aux changements d’amplitude et de fréquence de l’interférence. La procédure a été continuellement améliorée au fil des ans, et mise en œuvre dans des milliers d’instruments ECG et de systèmes assistés par ordinateur. Des approches similaires ont également été publiées par d’autres chercheurs .
- Principes
- Critère linéaire
- Compensation des variations d’amplitude du PL
- Filtrage linéaire
- Compensation de la variation de la fréquence PL
- Évaluation de l’efficacité de la procédure
- Influence du bruit EMG
- Suppression des interférences dans l’ECG haute résolution
- Cas des dispositifs alimentés par batterie et des systèmes ECG assistés par ordinateur
- Adaptation automatique à la fréquence nominale PL
- Développement de la procédure théorique
Principes
La procédure de soustraction est appliquée à l’origine avec la fréquence d’échantillonnage f S , un multiple de, et le matériel synchronisé avec la fréquence PL f PL . La procédure comprend les étapes suivantes :
-
Les segments ECG dont la bande de fréquence est proche de zéro sont détectés en continu à l’aide d’un critère approprié. Ils sont appelés segments linéaires et se trouvent principalement dans les intervalles PQ et TP, mais aussi dans les parties droites suffisamment longues des ondes R et T.
-
Les échantillons de ces segments sont moyennés en mouvement, c’est-à-dire soumis à un filtre peigne de phase linéaire dont le premier zéro est fixé à f PL . Ainsi, les échantillons filtrés ne contiennent pas d’interférence.
-
Les amplitudes d’interférence, appelées corrections, sont calculées pour chacun des échantillons verrouillés en phase, n, dans la période PL, T PL , en soustrayant les échantillons filtrés des échantillons correspondants du signal ECG contaminé (original).
-
L’ensemble des corrections obtenues est continuellement mis à jour dans les segments linéaires et utilisé dans les segments non linéaires (généralement autour des complexes QRS et des ondes T de forte amplitude) pour soustraire les interférences du signal ECG original.
L’un des premiers résultats obtenus par la méthode de soustraction est illustré à la figure 1 . Des interférences ont été ajoutées à un signal ECG simulé propre afin d’évaluer les erreurs et l’efficacité de la méthode.
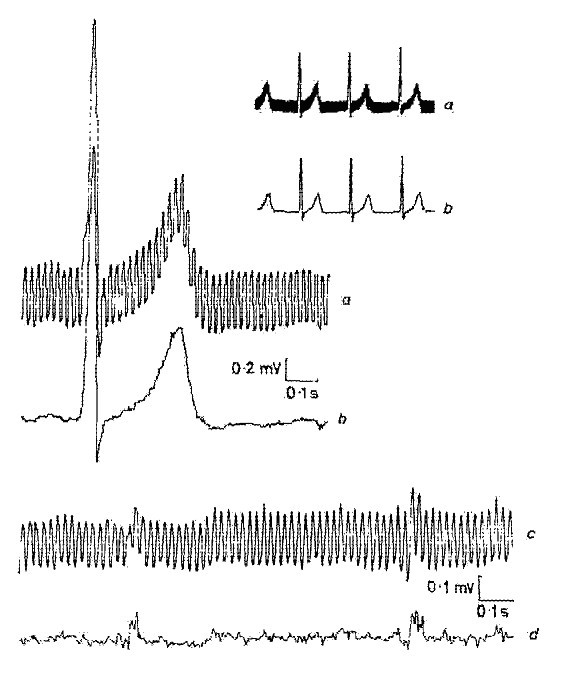
Un des premiers résultats obtenus par la procédure de soustraction.
Critère linéaire
Un critère linéaire, Cr, correspond généralement à la deuxième différence du signal (évaluation mathématique de la linéarité). Le premier Cr est défini de la manière suivante. Six premières différences consécutives, FD i , sont calculées en utilisant des échantillons de signal, X i , espacés d’un T PL :
FD i = X i+n – X i , pour i = 1 … 6 (1)
L’interférence PL dans les premières différences est supprimée si n = f S /f PL . Dans ce cas, n = 5, car la procédure a été développée initialement pour des valeurs nominales f PL = 50 Hz et f S = 250 Hz. En outre, les valeurs maximales FD max et minimales FD min sont prises pour déterminer Cr:
Cr = | FD max – FD min | <M, (2)
où M est la valeur seuil.
Des segments linéaires et non linéaires typiques sont représentés sur la figure 2. Le signal ECG réel (trace a) est superposé par des interférences (trace b). Les segments linéaires comprennent le signal basse fréquence et les composantes de fréquence de la ligne électrique. Un spectre de fréquence approximatif de ces segments linéaires est représenté sur la figure 3.

Sections linéaires et non linéaires typiques dans un signal ECG réel.
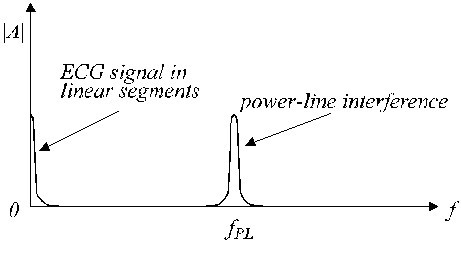
Spectre de fréquence approximatif d’un segment linéaire.
Ce critère fonctionne avec précision, mais peut difficilement être appliqué en temps réel en raison de sa mise en œuvre relativement lente. Cet inconvénient est surmonté par Christov et Dotsinsky qui utilisent un critère modifié de seulement deux différences ultérieures.
Cr = | FDi+1- FD i | <M. (3)
Le premier échantillon, qui ne remplit pas l’équation (3), est associé au début d’un segment non-linéaire. Dans la transition non-linéaire à linéaire, l’équation (3) doit être satisfaite consécutivement n fois afin d’éviter une détection prématurée du segment linéaire. Le critère est mis en œuvre en temps réel pour f S = 400 Hz et n = 8.
Plus tard, Dotsinsky et Daskalov ont défini le critère comme deux différences non consécutives :
Cr = |FDi+k- FD i | <M, pour k >1 (4)
Cette approche rend la transition du segment linéaire au segment non linéaire plus précise.
Compensation des variations d’amplitude du PL
Plus les corrections sont mises à jour fréquemment, meilleure est la compensation des variations d’amplitude du PL. Par conséquent, le seuil du critère linéaire, M, doit être raisonnablement moins restrictif pour que les erreurs, commises en faisant la moyenne de certains segments qui s’écartent du signal linéaire idéal, soient plus petites que les erreurs, qui apparaîtront si M déclenche une mise à jour sporadique de la correction. Initialement, M a été fixé à 160 μV . Plus tard, des valeurs heuristiques se sont avérées être M = 150 μV et M = 100 μV .
Filtrage linéaire
Pour un nombre impair d’échantillons n = 2m + 1 dans une période de l’interférence PL, la valeur filtrée :
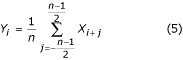
est en coïncidence de phase avec celle non filtrée.
En cas de nombre pair n = 2m, les deux valeurs sont déphasées d’une moitié de la période d’échantillonnage :
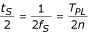
mais deviennent en coïncidence de phase en utilisant la formule
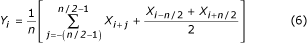
Il est possible de prendre pour la moyenne chaque deuxième, troisième ou qième échantillon si n/q est entier. Selon que n/q est impair ou pair, on utilise respectivement l’équation (7) ou (8).

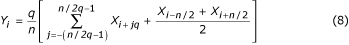
Un cas particulier de réduction maximale de l’échantillon se présente avec q = n/2 . La formule correspondante:
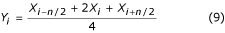
est appelée filtre « trois points ». En plus de l’équation (8), la formule suivante
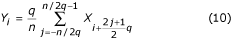
peut également être appliquée si q est pair. Dans le cas où q = n/2, le filtre devient ‘deux points’ et est représenté par :

La réduction du nombre d’échantillons dans une période de l’interférence entraînera une amélioration de la pente raide des lobes du filtre en peigne et raccourcira le temps de calcul. Cependant, ces « avantages » doivent être évalués avec soin afin de ne pas violer la règle de Nyquist avec une grande quantité de la troisième harmonique présente. Les autres harmoniques ne sont pas pris en considération puisque les harmoniques impairs les plus élevés sont généralement supprimés par des filtres passe-bas avec une coupure dans la gamme de 100-150 Hz, tandis que les pairs sont pratiquement absents en raison de la fabrication précise des pôles des générateurs des centrales électriques.
Compensation de la variation de la fréquence PL
La déviation autorisée de la fréquence PL nominale est limitée dans certains pays jusqu’à 1% par les normes. Dans la pratique, la déviation est souvent plus élevée. Kumaravel et al. ont signalé une variation de 3%. McManus et al. ont trouvé des changements considérables dans la fréquence d’interférence, qui est superposée aux enregistrements provenant de la base de données des normes communes pour l’électrocardiographie (CSE).
Les variations de fréquence conduisent à un cas particulier d’échantillonnage non multiple avec n réel, au lieu d’un entier. Cette complication peut être contournée si les écarts sont détectés par une mesure matérielle continue de f PL et corrigés par de petits ajustements de l’intervalle d’échantillonnage t S autour de sa valeur nominale (R), t RS = T RPL /n (ici, T RPL = 20 ms est le T PL nominal pour f RPL = 50 Hz). Pour f PL , écart compris entre 49,5 et 50,1 Hz, les variations de t S sont de l’ordre de 1%, et par conséquent elles n’introduisent pas d’erreurs au-delà de la précision de mesure admise des paramètres habituellement utilisés pour la classification automatique de l’ECG.
Une première approche associe le déclenchement de chaque premier échantillon, S 1 , des séquences S k (k = 1, 2…n) dans les périodes T PL avec une amplitude arbitraire choisie mais constante de la tension PL. Les échantillons suivants, S k (k = 2…n), sont espacés de t S , qui est obtenu par t S = T RTL /n. Pour 50 Hz, et n = 5, t S = 4 ms. Deux types d’erreurs commises par cette approche sont étudiés par Dotsinsky et Daskalov . La première, due aux irrégularités inter-échantillons, peut atteindre 1% à f S = 400 Hz et 1,2% à f S = 250 Hz, en cas de déviation de 1% autour de la f RPL . Le deuxième type d’erreur ne dépasse pas 3% et est une conséquence de l’emplacement décalé supplémentaire de l’échantillon filtré.
Dotsinsky et Daskalov ont rapporté une approche améliorée. La période continue T PL est mesurée et divisée par n. Le t S obtenu est utilisé dans le T PL suivant .
Évaluation de l’efficacité de la procédure
Des exemples de procédure de soustraction sont présentés à la figure 4 et à la figure 5. Les signaux ECG sont extraits de la base de données de l’American Heart Association. Les signaux sont filtrés par un filtre coupe-bande pour supprimer les interférences de 60 Hz (fréquence PL aux États-Unis). Ensuite, les signaux sont mélangés avec des interférences de 50 Hz, modulées en amplitude de 0 à 3,2 mVp-p par un taux de balayage de 200 μVs-1. Les traces sont identifiées comme suit : i) signal d’entrée ; ii) interférence synthétisée ; iii) signal mélangé ; iv) signal traité ; v) différence entre les signaux originaux et traités et vi) différence zoomée. En fait, les composantes supprimées comprennent également des bruits électromyographiques (EMG) et autres. Une partie non supprimée du signal, ainsi que de petites interférences résiduelles et des distorsions dues au compromis avec la valeur M sont également présentes dans les différences.
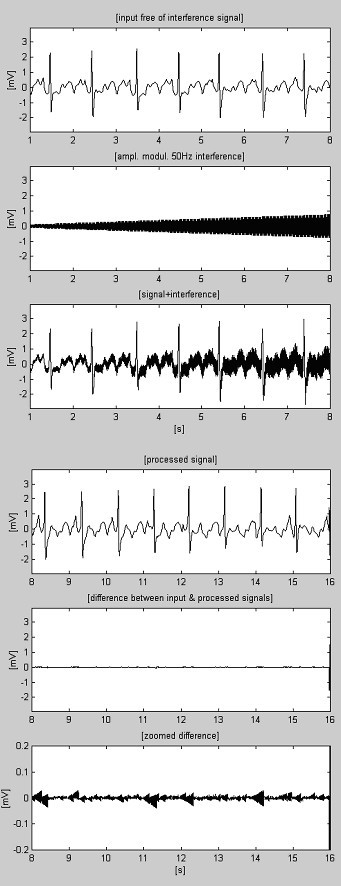
Enregistrement AHA 3004d1 traité.
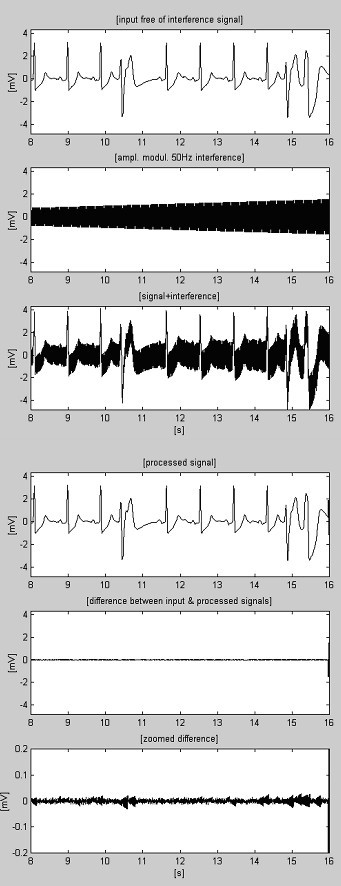
Traitement de l’enregistrement AHA 6007d1.
Deux signaux sont utilisés pour évaluer l’efficacité de la procédure de soustraction par rapport aux interférences uniquement. Le premier, issu de notre propre base de données, est dit conditionnellement » propre » (figure 6). Le résultat montre de petites différences entre les signaux d’entrée et les signaux traités, visuellement dues au bruit présent dans l’entrée. Ce résultat est vérifié avec le second signal synthétisé, qui ne contient aucune perturbation (Fig. 7). Comme on peut le constater, aucune distorsion n’est introduite. Le même signal synthétisé est superposé par des interférences et traité (Fig. 8). Aucune interférence résiduelle ne peut être trouvée.
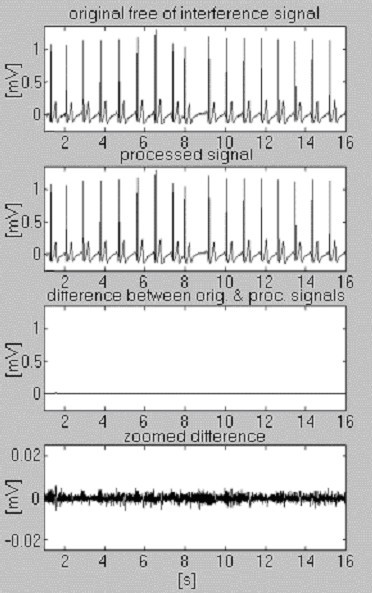
Traitement du signal conditionnellement « propre ».
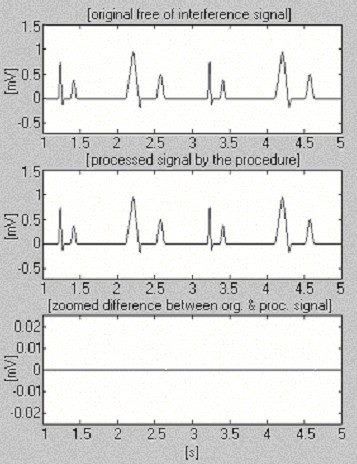
Traitement du signal synthétisé.
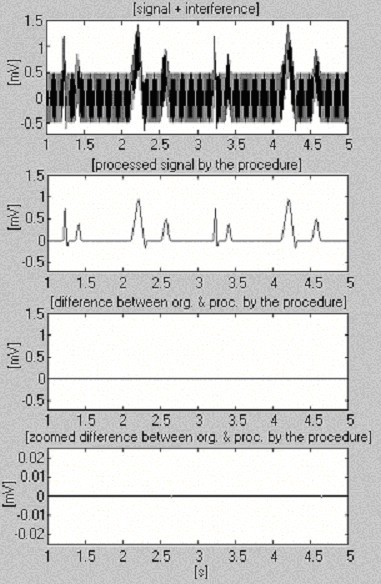
Traitement du signal synthétisé+interférence.
Influence du bruit EMG
Parfois, le bruit EMG est si élevé que la recherche du segment linéaire est entravée. En conséquence, des corrections imprécises, qui ne correspondent pas au dernier changement de l’amplitude de l’interférence, provoqueront des erreurs (voir le bruit résiduel entre la 11e et la 14e s dans la figure 9).
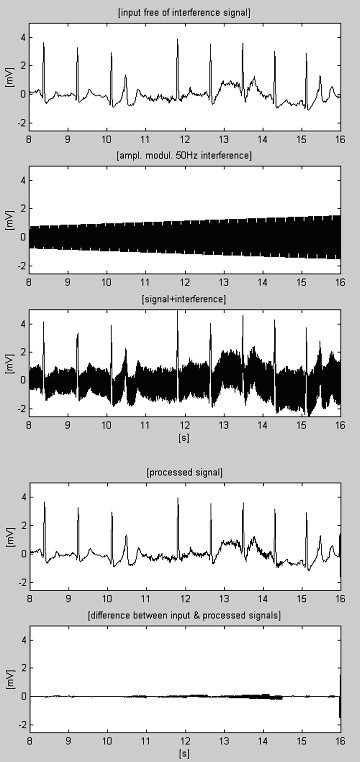
Signal ECG traité+bruit EMG+interférence.
Une approche très simple pour la suppression de l’influence du bruit EMG sur la procédure introduit un tampon parallèle supplémentaire où les parties en cours du signal sont moyennées sans condition . Ce tampon est utilisé pour une détection précise de la linéarité. La figure 10 et la figure 11 montrent la comparaison des résultats sans et avec le tampon parallèle. Les traces ‘a’ représentent un signal ECG mélangé à des interférences et au bruit EMG. Les traces ‘b’ de la Fig. 10 et ‘c’ de la Fig. 11 indiquent les transitions entre les segments linéaires et non linéaires (fonctions on-off). Comme on peut le voir, la partie du signal moyenné de la Fig. 10 est très limitée. Par conséquent, l’efficacité de la procédure est réduite (Fig. 10c et 10d. En revanche, le tampon parallèle permet la détection de longs segments linéaires (Fig. 11c et le bruit résiduel dans le signal traité (Fig. 11d est faible. Cependant, le bruit n’est pas totalement supprimé car une partie de celui-ci participe au calcul de correction.
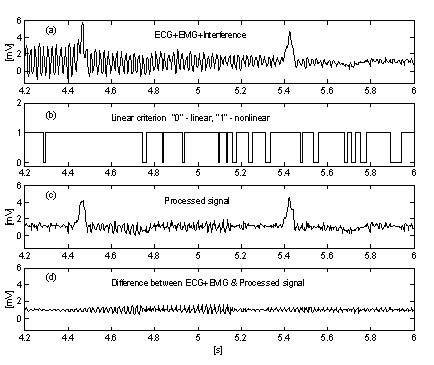
Soustraction du bruit interférence+EMG sans tampon parallèle.
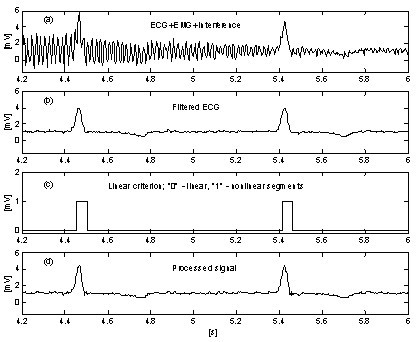
Soustraction du bruit interférence+EMG avec tampon parallèle.
Une amélioration supplémentaire de la suppression du bruit EMG est obtenue par Christov en utilisant une valeur de seuil adaptative M, qui est calculée par rapport au rapport bruit/signal Rt, défini comme Rt = S NL /S F , où le niveau de bruit S NL est égal à la largeur sommaire des segments non linéaires dans une époque S F , correspondant approximativement à l’intervalle RR considéré. La recherche de linéarité avec un critère de M = 150 μV pour un ECG » propre » (figure 12a) et pour le même signal, mais contaminé par le bruit EMG (figure 12b) montre différents S NL , (figures 12c et 12d). La méthode est développée dans l’environnement MATLAB. Le seuil initial M est choisi égal à 30 μV. Ensuite, il est progressivement augmenté jusqu’à ce que Rt atteigne 10%, après quoi la procédure de soustraction est lancée. Le niveau Rt ≤ 0,1 valeur est suggéré par le rapport ‘largeur du QRS par rapport à son intervalle RR’, qui est généralement autour de 10%. L’élimination à la fois des interférences et du bruit EMG peut être observée sur les figures 13b et 13d, où M = 420 μV est utilisé. Pour comparaison, le signal ECG ‘propre’ est traité avec M = 35 μV (Fig. 13a et 13c).

Niveaux de bruit SNL (traces c et d) dans le signal ECG ‘propre’ (trace a) et le signal contaminé par l’EMG (trace b), respectivement.
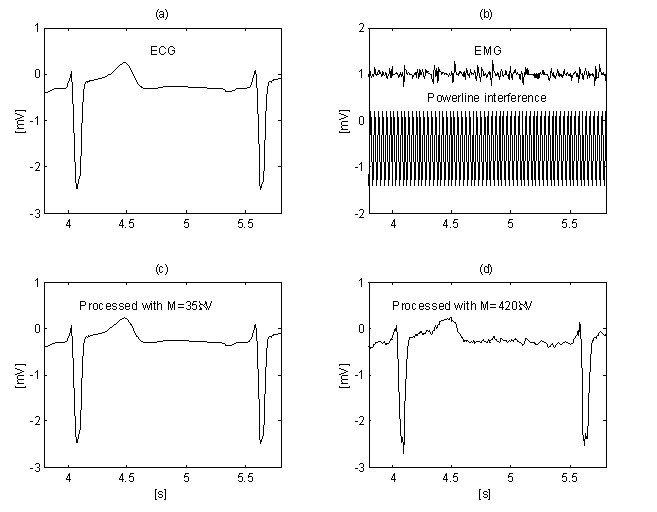
Suppression du bruit interférence+EMG en utilisant un seuil adaptatif M : ‘signal propre’ (a) traité avec M = 35 μV (c) et signal contaminé (b) soumis à la procédure avec M = 420 μV (d).
Les segments linéaires ne peuvent pas être trouvés régulièrement chez les patients atteints de fibrillation auriculaire et ventriculaire. Cependant, la préservation totale de la forme de l’onde n’est pas nécessaire pour la détection de la fibrillation et, par conséquent, toutes sortes de filtres traditionnels peuvent être appliqués.
Suppression des interférences dans l’ECG haute résolution
La procédure de soustraction n’est pas directement applicable à l’ECG de His de surface du corps, car l’onde de His de faible amplitude et de fréquence relativement basse ne peut pas être distinguée dans les segments linéaires. Ainsi, l’onde de His sera, en pratique, supprimée ou même éliminée du signal. Le bruit de l’EMG est généralement d’une plus grande amplitude et d’une fréquence beaucoup plus élevée que l’onde de His de surface. Par conséquent, la simple modification de la valeur seuil, M, ne permet pas d’obtenir une délimitation acceptable des segments linéaires et non linéaires.
Bazhina et al. ont mis en œuvre la modification suivante. Le début du segment non linéaire détecté avant un complexe QRS est décalé de 100 ms vers la gauche, définissant ainsi la région de l’onde de His comme un segment non linéaire par défaut (figure 14).
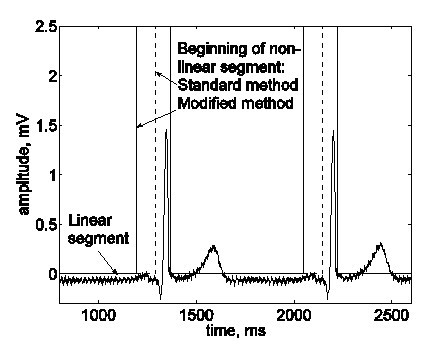
Le début d’un segment non linéaire incluant le complexe QRS a été décalé par défaut de 100 ms vers la gauche, pour inclure la zone où l’onde de His est censée apparaître.
La procédure de soustraction et trois autres méthodes : filtres coupe-bande, interpolation spectrale , et soustraction par régression sont testées par rapport à une distorsion minimale du signal original . Les procédures de soustraction et de régression-soustraction se sont avérées les meilleures, car Baratta et al utilisent un concept similaire pour l’estimation du bruit dans les segments linéaires. La régression-soustraction traite mal les changements d’amplitude de l’interférence dans le segment actuel.
Cas des dispositifs alimentés par batterie et des systèmes ECG assistés par ordinateur
La mesure matérielle de f PL , nécessaire pour la compensation de la modulation de fréquence de l’interférence, n’est pas réalisable dans les dispositifs alimentés par batterie et dans certains systèmes ECG assistés par ordinateur. Dotsinsky et Stoyanov ont étudié la gamme des changements de fréquence de l’interférence avec une amplitude constante, pour laquelle la partie résiduelle est limitée à des niveaux acceptables sans utilisation de l’échantillonnage synchronisé. Ils ont constaté que des interférences résiduelles inférieures à 20 μVp-p pouvaient être obtenues avec la procédure par : i) amplitude d’interférence ≤ 0,4 mVp-p et ii) changement de fréquence avec un taux ≤ 0,0125 Hzs-1. Comme de telles exigences pour l’alimentation peuvent souvent être dépassées, un logiciel de mesure des interférences a été développé.
Le signal ECG est traité initialement par un filtre passe-bande de 49-51 Hz. Les amplitudes de deux échantillons adjacents, Br L et Br R , prélevés sur une pente positive de l’interférence, située en dessous et au-dessus de la ligne zéro, sont mesurées (figure 15). La distance, t CP , entre le point de croisement CP et l’échantillon de droite, Br R , est calculée continuellement par :
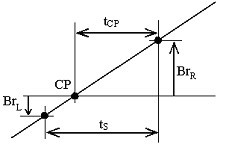
Traversée du zéro de l’interférence.

En cas de changement de T PL, t S est redéfini en utilisant

Cette approche a été mise en œuvre dans l’environnement MATLAB. Pour une fréquence d’échantillonnage f S = 500 Hz et f RPL = 50 Hz, n est égal à 10. Le produit kn détermine le temps qu’il est recommandé d’écouler avant de calculer et de substituer le nouveau tCP,i + kn au précédent tCP,i. La figure 16 montre un signal ECG de 1 mV traité après avoir été mélangé par interférence avec une amplitude constante de 2 mVp-p et une fréquence extrêmement rapide variant de 1 Hz par 8 s (première trace). Afin d’évaluer l’efficacité obtenue, la différence zoomée sans échantillonnage synchronisé (dernière trace) est également présentée.
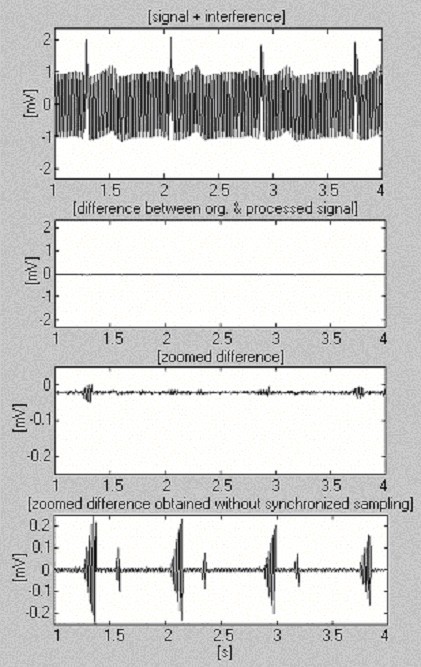
Procédure de soustraction utilisant la mesure de fréquence par courant porteur du logiciel.
La prochaine étape logique à suivre consiste à : i) conserver le t S nominal de l’instrument ECG, ii) ré-échantillonner le signal en fonction de la f PL mesurée en cours afin d’éliminer l’interférence et iii) revenir au t S nominal. Les premiers résultats d’une telle approche sont très prometteurs. Ainsi, la compensation logicielle de la variable f PL , ainsi qu’une mise en œuvre totale de la procédure de soustraction dans un instrument, y compris le réglage automatique pour des f RPL de 50 ou 60 Hz, seront réalisées indépendamment des circuits matériels et des logiciels correspondants.
Adaptation automatique à la fréquence nominale PL
Un programme commun de soustraction des interférences alternatives en environnement 50 et 60 Hz conduit à un échantillonnage non multiple, c’est-à-dire à un n réel. Les valeurs de t S largement utilisées pour f RPL = 50 Hz, telles que 250, 500 et 1000 Hz, correspondent à des n irrationnels de 4,1(6), 8,3(3) et 4,1(6) si l’on doit éliminer les interférences de 60 Hz. Dans le cas inverse, f S = 360 Hz nécessite n = 7,2. Les valeurs arrondies n* sont inacceptables à utiliser, car elles introduiraient une erreur considérable.
Une solution très simple ne nécessitant pas de changement de f S a été trouvée par Dotsinsky et Stoyanov . La procédure originale applique un filtre en peigne sur une période, T PL , de l’interférence. Ainsi, le programme s’exécute plus rapidement. En général, n peut être pris parmi k > 1 périodes entières. La procédure est exploitée si :
n = kT PL /t S est un entier.
Pour t S = 2 ms (f S = 500 Hz) et f RPL = 50 Hz, la plus petite valeur de k satisfaisant l’équation (14) est en réalité k = 1. Cependant, dans le cas de 60 Hz, k est égal à 3. Des zéros associés aux sous-harmoniques 20 et 40 Hz apparaîtront également mais ils n’ont aucune influence sur la procédure. Il suffit donc de commuter n entre 10 (k = 1) et 25 (k = 3) pour fonctionner avec les deux interférences. A cet effet, deux filtres passe-bande numériques contrôlent le signal entrant. La figure 17 montre que le filtre dont la bande de fréquence chevauche l’interférence génère un signal de sortie d’un ordre de grandeur plus élevé que l’autre filtre.
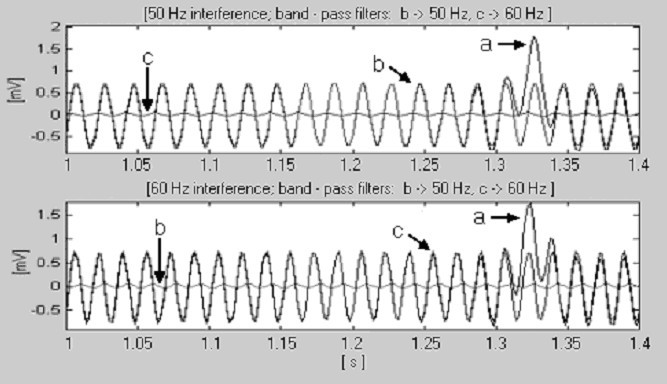
Détection de la fréquence nominale de la ligne électrique, a) partie du complexe QRS, b) interférence 50 Hz et c) interférence 60 Hz.
Développement de la procédure théorique
La théorie de la procédure de soustraction a été développée plus avant par Mihov , Levkov et Mihov , et Mihov et al . Ils ont proposé quatre types de filtres, mis en œuvre dans une structure généralisée qui peut surmonter les problèmes avec presque tous les cas d’échantillonnage non multiple, y compris les variations de fréquence d’interférence, sans utiliser la conversion AD synchronisée.
Le filtre dit D en échantillonnage multiple est défini comme est Cr dans l’équation (2), où la deuxième différence, D i , est obtenue avec des FD s qui sont espacés d’un T PL :
D i = (X i+n – X i ) – (X i – X i-n ) = X i-n – 2X i + X i+n (15)
La fonction de transfert du filtre D présente des zéros à f = 0 et f = f PL Hz, qui est représentée égale à 50 Hz sur la Fig. 18.

Fonction de transfert du filtre D pour fPL = 50 Hz.
Le filtre K décrit la moyenne mobile présentée par les équations (5) et (6). Sa fonction de transfert est donnée à la figure 19 pour n = 5 dans le cas d’une multiplicité impaire.
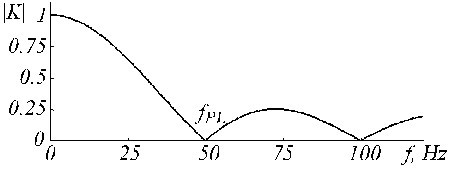
Fonction de transfert du filtre K pour fPL = 50 Hz et n = 5.
L’équation utilisée pour le calcul continu des composantes de l’interférence:
B i = X i – Y i (16)
définit en fait un filtre numérique appelé filtre (1-K).
De plus, les filtres sont redéfinis pour un échantillonnage non multiple, et f S = 250 Hz en conjonction avec f RPL = 60 Hz est pris en considération pour illustrer l’amélioration du logiciel.
Pour préserver les zéros de la fonction de transfert, le filtre D doit être soustrait avec un filtre de correction avec un zéro à f = 0 et un gain de D RPL à f = f RPL , égal au gain du filtre D pour la même fréquence, f RPL . La synthèse du filtre de correction est basée sur un filtre auxiliaire à trois points donné par l’équation :

où (n/2)* est la valeur arrondie de n/2.
Puisque A RPL est le gain du filtre auxiliaire pour f = f RPL , le filtre de correction est multiplié par le rapport D RPL /A RPL . En utilisant les fonctions de transfert correspondantes, D RPL et A RPL sont calculés à l’avance par :
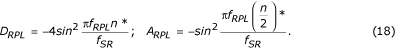
Finalement, le filtre D* corrigé est présenté comme

et est représenté sur la figure 20 par la trace ‘c’, où les traces ‘a’ et ‘b’ sont le filtre D et le filtre de correction, respectivement.
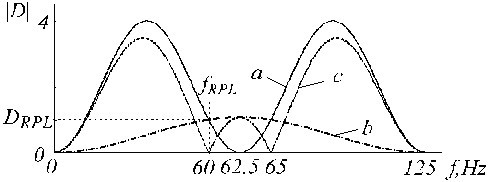
Fonctions de transfert de a) filtre D, b) filtre de correction auxiliaire et c) filtre D corrigé.
La fonction de transfert du filtre K doit préserver le zéro pour f = f RPL , le gain unitaire pour f = 0 et une réponse en phase linéaire. La procédure de correction du filtre K est similaire à la précédente. Un filtre auxiliaire est donné par la formule utilisée pour le calcul des corrections :
A i = X i – Y i , (20)
Le gain du filtre est égal à 1 – K RPL pour f = f RPL , où K RPL est le gain du filtre K pour la même fréquence f RPL . Le filtre auxiliaire est multiplié par K RPL /(1 – K RPL ) et soustrait du filtre K. L’équation du filtre K* corrigé est :
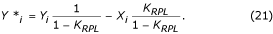
La constante K RPL peut être estimée par :

pour la multiplicité impaire ou paire, respectivement.
Un exemple de correction du filtre K est illustré à la figure 21, où les traces ‘a’, ‘b’ et ‘c’ représentent le filtre K primaire, le filtre auxiliaire et le filtre K* corrigé.
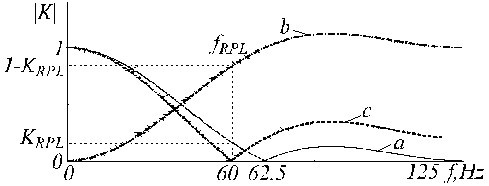
Fonction de transfert de a) filtre K, b) filtre auxiliaire de correction et c) filtre K corrigé.
Dans le cas d’un échantillonnage non multiple, une différence de phase apparaît entre les échantillons ECG en cours et les composantes d’interférence B i (équation 16) généralement situées dans un tampon temporaire premier entré-premier sorti (FIFO). Par conséquent, B i doit être modifié en étant soustrait des échantillons ECG pendant les segments non linéaires. La procédure de compensation est relativement compliquée. La figure 22 montre le contenu du tampon temporaire. L’échantillon d’interférence actuel, B i-n *, ne coïncide pas avec l’échantillon restauré, B i . Son amplitude doit être recalculée afin de compenser la différence de phase entre eux. Pour ce faire, on utilise un nouveau filtre à réponse de phase linéaire et à gain unitaire pour f = f RPL , appelé filtre B. Il est synthétisé à partir de l’échantillon connu, le filtre B, qui est un filtre à réponse de phase linéaire. Il est synthétisé à partir du filtre K connu, avec une fenêtre égale à la période de brouillage. Dans le cas d’un n* impair, il peut être décrit comme:
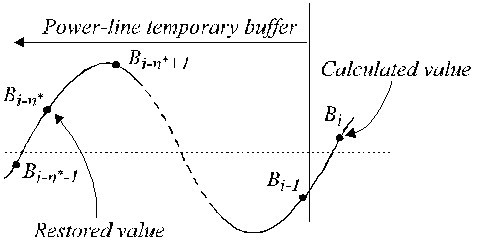
Valeurs restaurées dans le tampon temporaire.
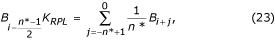
où K RPL est le gain pour l’interférence du filtre de moyennage donné par l’équation (22).
La valeur de tampon restaurée B i peut être calculée par :
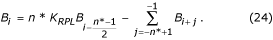
En cas de n* pair :
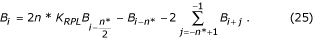
La fonction de transfert du filtre B est représentée sur la figure. 23.
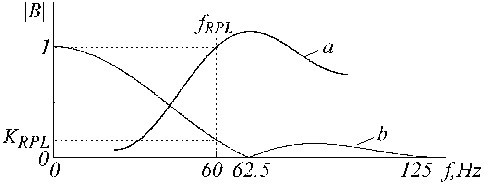
Fonctions de transfert du a) filtre B et b) du filtre K connu.
La structure généralisée est présentée dans la Fig. 24, où les modules de la procédure de soustraction sont les suivants:
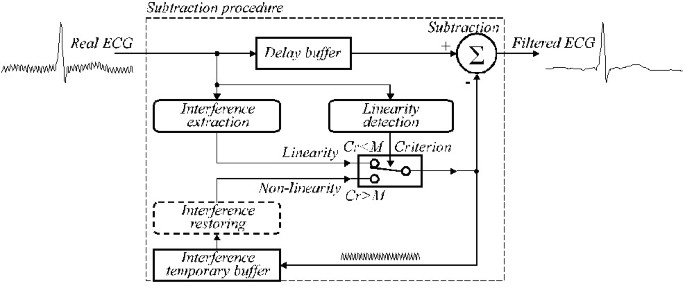
Structure généralisée de la procédure de soustraction.
-
Détection de la linéarité. Le filtre D est appliqué pour évaluer la linéarité de chaque voisinage d’échantillons de signaux.
-
Extraction des interférences. Le filtre (1-K) est utilisé pour calculer la composante d’interférence.
-
Critère. La condition Cr <M envoie l’interférence PL extraite ou restaurée à la soustraction.
-
Tampon temporaire d’interférence. La composante d’interférence extraite ou restaurée utilisée comme correction dans le segment non linéaire est sauvegardée à la position verrouillée avec la phase en cours de l’interférence de la ligne électrique.
-
Restauration de l’interférence. Le filtre B est appelé en cas d’échantillonnage non multiple afin de restaurer les vraies valeurs de correction, qui doivent être soustraites des échantillons du signal d’entrée dans les segments non linéaires.
-
Tampon de retard. Compense le retard, qui apparaît avec le filtre D et le filtre (1-K) et est impératif si la procédure est exécutée en temps quasi-réel. Dans le cas contraire, le tampon pourrait ne pas être pris en compte.
-
Soustraction. La valeur d’interférence extraite ou restaurée est soustraite du signal d’entrée retardé pour sortir un signal ECG « propre ». En cas de non-linéarité, l’extraction et la soustraction des interférences mettent en œuvre le filtre K.
Un algorithme amélioré selon la structure généralisée a été testé hors ligne. Les résultats pour f S = 250 Hz et f RPL = 60 Hz sont présentés sur la figure 25.
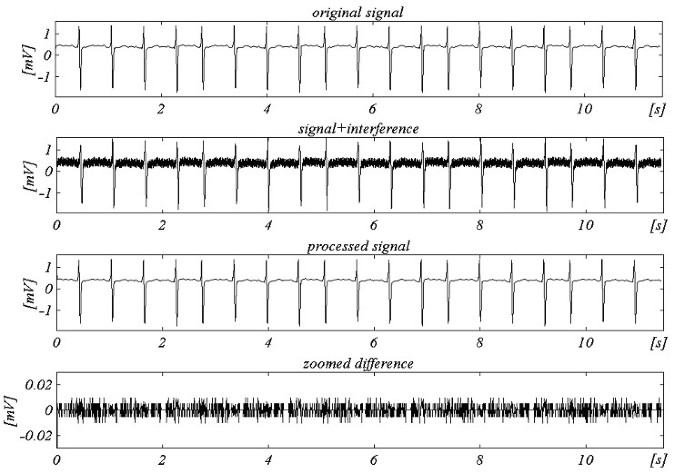
Exemple pour un échantillonnage non multiple avec fRPL = 60 Hz et fS = 250 Hz.
.