A harmadik törvény azt állítja, hogy egy anyag entrópiája mindig véges, és hogy a hőmérséklet nullához közeledve állandóhoz közelít. Ennek az állandóságnak az értéke független az anyagot jellemző egyéb állapotfüggvények értékeitől. Bármely adott anyag esetében tetszőlegesen választott értéket rendelhetünk a nulla hőmérsékletű határértékhez. Nem rendelhetünk azonban minden anyaghoz tetszőleges nulla hőmérsékletű entrópiát. A hozzárendeléseknek összhangban kell lenniük a különböző anyagok közötti reakciók entrópiaváltozásának kísérletileg megfigyelt zérushőmérsékleti határértékeivel. Tökéletesen kristályos anyagok esetében ezek a reakcióentrópiák mind nulla. Ezt a feltételt úgy tudjuk teljesíteni, hogy az egyes elemek nulla hőmérsékletű moláris entrópiájához tetszőleges értéket rendelünk, és kikötjük, hogy bármely vegyület nulla hőmérsékletű entrópiája az alkotóelemek nulla hőmérsékletű entrópiáinak összege. Ez a számítás jelentősen leegyszerűsödik, ha minden elem zérushőmérsékleti entrópiája nulla. Ez a harmadik törvény lényeges tartalma.
A Lewis és Randall-féle kijelentés magába foglalja az entrópiák nulla entrópiás referenciaállapotának ezt a kiválasztását, minden elem nulla fokos “kristályos állapotaként” határozva meg. Ennek eredményeként bármely anyag entrópiája nulla fokon nagyobb vagy egyenlő nullával. Vagyis a Lewis és Randall-féle kijelentés olyan egyezményt tartalmaz, amely rögzíti bármely anyag entrópiájának nulla hőmérsékletű határértékét. Ebben a tekintetben a Lewis és Randall-féle kijelentés lényegében önkényes döntést hoz, amely nem a természet belső tulajdonsága. Látjuk azonban, hogy ez egy túlnyomóan kényelmes választás.
Az első és a második törvény alternatív kijelentéseit tárgyaltuk. A harmadik törvény számos alternatív állítása is lehetséges. Megfontoljuk a következőket:
Az abszolút nulla hőmérsékletet lehetetlen elérni.
Ez az állítás általánosabb, mint a Lewis és Randall-féle állítás. Ha megvizsgáljuk ennek az állításnak az egyetlen anyagot érintő folyamatokban elérhető hőmérsékletekre való alkalmazását, akkor megmutathatjuk, hogy ez a Lewis és Randall-féle állítást feltételezi, illetve feltételezi.
A hőkapacitás \(C_P\) tulajdonságai központi szerepet játszanak ezekben az érvekben. Láttuk, hogy \(C_P\) a hőmérséklet függvénye. Bár nem célszerű ezt megtenni, az \(C_P\) meghatározó összefüggését alkalmazhatjuk egy fázisátalakuláson átmenő anyagra, és \(C_P=\infty\). Ha olyan anyagra gondolunk, amelynek hőkapacitása kisebb, mint nulla, akkor a hővel és a hőmérséklettel kapcsolatos alapvető elképzeléseink ellentmondásával találkozunk: Ha \(q>0\) és \({q}/{\Delta T}<0\), akkor \(\Delta T<0\) kell, hogy legyen; vagyis ha az anyagot melegítjük, akkor a hőmérséklete csökken. Röviden, az általunk kidolgozott elmélet olyan premisszákat foglal magába, amelyek \(C_P>0\) értéket követelnek meg minden olyan rendszerre, amelyen méréseket tudunk végezni.
Jellemezzünk egy tiszta anyagú rendszert a nyomással és a hőmérséklettel, és tekintsünk megfordítható állandó nyomású folyamatokat, amelyekben csak nyomás-térfogat munka lehetséges. Ekkor \({\left({\partial S}/{\partial T}\right)}_P={C_P}/{T}\) és \(dS={C_PdT}/{T}\). Most meg akarjuk mutatni: a Lewis és Randall-féle kikötés, miszerint az entrópia mindig véges, megköveteli, hogy a hőkapacitás nullára menjen, amikor a hőmérséklet nullára megy. (Mivel meg fogjuk mutatni, hogy a harmadik törvény tiltja az abszolút nullánál történő méréseket, ez a következtetés összhangban van az előző bekezdésben leírt következtetésünkkel.) Az, hogy a hőkapacitás nullára megy, amikor a hőmérséklet nullára megy, nyilvánvaló a \(S={C_PdT}/{T}.\) Ha \(C_P\) nem megy nullára, amikor a hőmérséklet nullára megy, akkor \(dS\) tetszőlegesen nagy lesz, amikor a hőmérséklet nullára megy, ami ellentmond Lewis és Randall állításának.
Hogy ezt az eredményt kifejezettebben fejtsük ki, legyen a hőkapacitás \(T\) és nulla hőmérsékleten \(C_P\ balra(T\jobbra)\), illetve \(C_P\ balra(0\jobbra)\). Mivel \(C_P\left(T\right)>0\) bármely \(T\ >\ 0\) esetén, \(S\left(T\right)-S\left(T^*\right)>0\) bármely \(T>T^*>0\) esetén. Mivel az entrópia mindig véges, \(\infty >S\left(T\right)-S\left(T^*\right)>0\), így
\\ }>0\]
és
\
A nullához közeli hőmérsékletekre, a hőkapacitást tetszőleges pontossággal \(T\) Taylor-soros polinomként fejezhetjük ki:
\
Az egyenlőtlenségek a következők lesznek:
\
A bal oldali feltétel \(C_P\left(0\right)=0\).
A harmadik törvényt tekinthetjük úgy is, mint a tiszta anyagok hőkapacitására vonatkozó állítást. Nemcsak arra következtetünk, hogy \(C_P>0\) minden \(T>0\) esetén, hanem arra is, hogy
\
Még általánosabban, a nem tiszta anyagokból álló zárt, reverzibilis rendszerekre is következtethetünk megfelelő állításokat: \({\left({\partial H}/{\partial T}\right)}_P>0\) minden \(T>0\) esetén, és \({\mathop{\mathrm{lim}}_{T\to 0} T^{-1}{\left({\partial H}/{\partial T}\right)}_P=0\ }\). (Az ilyen rendszerek zérushőmérsékleti entrópiája azonban nem nulla.) Az alábbi tárgyalásban a rendszert tiszta anyagként írjuk le. Lényegében ugyanezeket az érveket bármelyik rendszerre alkalmazhatjuk; csak \(C_P\) helyett \({\left({\partiális H}/{\parciális T}\right)}_P\) kell használnunk. A Lewis és Randall-féle állítás azt állítja, hogy az entrópia az abszolút nullponton állandóvá válik, függetlenül bármely más termodinamikai függvény értékétől. Ebből következik, hogy az entrópia nulla fokon független a nyomás értékétől. Bármely két nyomás, \(P_1\) és \(P_2\) esetén \(S\left(P_2,0\right)-S\left(P_1,0\right)=0\). Hagyjuk, hogy \({P=P}_1\) és \(P_2=P+\Delta P\) és, akkor
\
bármely \(\Delta P\) esetén. Ebből következően
\
A 10. fejezetben \({\left({\partial S}/{\partial }P\right)}_T=-{\left({\partial V}/{\partial T}\right)}_P\), tehát mind az entrópia, mind a térfogat aszimptotikusan közelít a zérushőmérsékleti értékéhez.
Amikor azt mondjuk, hogy az abszolút nulla elérhetetlen, azt értjük ezalatt, hogy egyetlen rendszer sem mehet át olyan változáson, amelyben a végső hőmérséklete nulla lenne. Hogy lássuk, miért kell elérhetetlennek lennie az abszolút nullpontnak, tekintsük azokat a folyamatokat, amelyek csökkenthetik egy rendszer hőmérsékletét. Általában különböző hőmérsékletű hőtárolók állnak rendelkezésünkre. Kiválaszthatjuk azt a rendelkezésre álló tározót, amelynek a hőmérséklete a legalacsonyabb, és egyszerű termikus érintkezéssel erre a hőmérsékletre hozhatjuk a rendszert. Ennyi triviális; nyilvánvaló, hogy a kihívás a hőmérséklet további csökkentése. Ehhez valamilyen más változtatást kell végrehajtanunk. Bármi legyen is ez a változás, nem segítheti elő a környezettel való hőcsere. Miután a rendszert a környezet leghidegebb elérhető részének hőmérsékletére hoztuk, minden további hőcsere a környezettel csak kontraproduktív lehet. Ebből arra következtetünk, hogy minden, a célunknak megfelelő folyamatnak adiabatikusnak kell lennie. Mivel egy adiabatikus folyamat nem cserél hőt a környezettel, \(\Delta \hat{S}=0\).
A folyamatnak is lehetséges folyamatnak kell lennie, tehát \(\Delta S+\Delta \hat{S}\ge 0\), és mivel adiabatikus, \(\Delta S\ge 0\). Tekintsünk egy reverzibilis és egy irreverzibilis folyamatot, amelyben ugyanaz a rendszer\({}^{2}\) az \(P_1\) és \(T_1\) által meghatározott állapotból egy második állapotba kerül, amelyben a nyomás \(P_2\). E folyamatok véghőmérsékletei és entrópiaváltozásai különbözőek. A reverzibilis folyamat esetében \(\Delta S=0\); a végső hőmérsékletet \(T_2\)-ként jelöljük. Az irreverzibilis folyamat esetében \(\Delta S>0\); a végső hőmérsékletet \(T^*_2\). Mint kiderül, az irreverzibilis folyamat esetében a hőmérsékletváltozás kisebb, mint a reverzibilis folyamat esetében; vagyis \(T_2-T_1<t^*_2-t_1\)>. Ennek megfelelően a reverzibilis folyamat alacsonyabb hőmérsékletet ér el: \({T_2<t}^*_2\)>. A
\
ből kiszámíthatjuk az entrópiaváltozásokat ezekre a folyamatokra. A reverzibilis folyamatra kiszámítjuk \
Ezért először kiszámítjuk
\
az \(P_1\), \(T_1\) állapotból az \(P_2\) és \(T_1\) által meghatározott állapotba történő izotermikus reverzibilis átalakulást. Erre a lépésre \(dT\) nulla, és így
\
Ezután kiszámítjuk
\
az \(P_2\), \(T_1\) állapotból az \(P_2\), \(T_2\) állapotba történő izobár reverzibilis átalakulásra. Ennél az átalakulásnál \(dP\) nulla, és
\
Mert,
\
Mivel \(\Delta S^{rev}=0\), a reverzibilis folyamat egyedi, azaz adott \(P_1\), \(T_1\) és \(P_2\) esetén a rendszer végső hőmérséklete meghatározott. Az \(T_2\) értéket a
\
\(T_2\)-ből találjuk meg
Az irreverzibilis folyamat entrópiaváltozásának megértéséhez először is megjegyezzük, hogy végtelen számú ilyen folyamat létezik. A véghőmérsékletben nincs semmi egyedi. Adott \(P_1\), \(T_1\) és \(P_2\), a végső hőmérséklet \(T^*_2\) bármilyen értéket felvehet, amely megfelel az anyag tulajdonságainak. Egy adott irreverzibilis folyamat meghatározásához mind a négy \(P_1\), \(T_1\), \(P_2\) és \(T^*_2\) mennyiséget meg kell adnunk. Miután azonban ezt megtettük, kiszámíthatjuk az irreverzibilis folyamat entrópiaváltozását,
\
azáltal, hogy kiszámítjuk az entrópiaváltozásokat, ahogyan a rendszert reverzibilisen végigvisszük az izotermikus kétlépcsős úton \(P_1\)-től, \(T_1\) és \(P_2\), \(T_1\) között, majd az izobár úton \(P_2\), \(T_1\) és \(P_2\), \(T^*_2\) között. Az \(\Delta S^{irrev}\) kiszámítása erre a \(P_1\), \(T_1\) és \(P_2\), \(T^*_2\) közötti reverzibilis útra ugyanazt a logikát alkalmazza, mint az előző bekezdésben az \(\Delta S\) kiszámítása az \(P_1\), \(T_1\) és \(P_2\), \(T_2\) közötti reverzibilis útra. A különbség az, hogy \(T^*_2\) helyettesíti \(T_2\) mint felső határértéket a hőmérsékleti integrálban. A nyomásintegrál ugyanaz. Van
\
Az \(\Delta S^{irrev}>\Delta S^{rev}\)-ből van
\
Mivel az integrálok azonosak és pozitívak, következik, hogy \(T^*_2>T_2\), ahogy fentebb állítottuk.
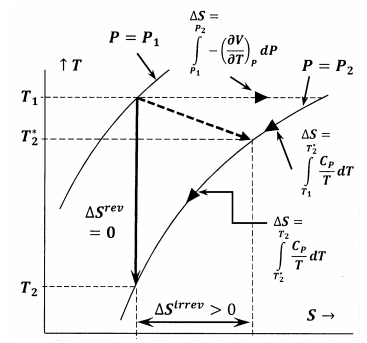
A 6. ábra az ebben az érvelésben tárgyalt különböző mennyiségek közötti összefüggéseket mutatja. A 6. ábra először a rendszer két izobárjának ábrázolását mutatja a hőmérséklet-entrópia térben. Azaz a \(P=P_1\) feliratú vonal a hőmérséklet-entrópia pontok azon halmazát ábrázolja, ahol az egyensúlyban lévő rendszerben \(P_1\) nyomás van; a \(P=P_2\) feliratú vonal pedig az \(P_2\) nyomáson lévő egyensúlyi helyzeteket ábrázolja. A vázlat többi vonala olyan pályákat jelöl, amelyek mentén a rendszer állandó entrópia vagy állandó hőmérséklet mellett reverzibilis változásokon mehet keresztül. A szaggatott vonal azt az irreverzibilis folyamatot ábrázolja, amelyben a rendszer a \(P_1\), \(T_1\) által meghatározott állapotból az \(P_2\), \(T^*_2\) által meghatározott állapotba kerül. Ez a vonal szaggatott, hogy jelezze azt a tényt, hogy a rendszer hőmérséklete nem biztos, hogy jól meghatározott az irreverzibilis folyamat során.
A hatékony hűtés nyomásváltozásokkal érhető el, ha a rendszer gáz. Folyadékok és szilárd anyagok esetében azonban \({\left({\partial V}/{\partial T}\right)}_P\) kicsi; következésképpen a hőmérsékletváltozás egy reverzibilis nyomásváltozás esetén szintén kicsi. Az abszolút nullához közeli hőmérsékleten szinte minden anyag szilárd; a hatékony hűtés eléréséhez olyan termodinamikai változót kell megváltoztatnunk, amelyre a szilárd anyag hőmérsékleti együtthatója a lehető legnagyobb. Ahhoz, hogy megvizsgáljuk egy rendszer hőmérsékletének a nyomáson kívül más változtatásával történő csökkentésének általános problémáját, olyan rendszert kell vizsgálnunk, amelyben a nyomáson kívüli térfogati munka valamilyen formája lehetséges. Egy ilyen rendszerre egy további erő hat, és energiája ennek az erőnek a változásával változik.
Adiabatikus demagnetizálás
Az adiabatikus demagnetizálásnak nevezzük azt a gyakorlati módszert, amellyel rendkívül alacsony hőmérsékleteket érhetünk el. Ez a módszer a paramágneses szilárd anyagok tulajdonságait használja ki. Az ilyen szilárd anyagokban az egyes atomokon lokalizált párosítatlan elektronok mágneses momentumot hoznak létre. A kvantummechanika fontos következtetéseket von le az ilyen mágneses momentumok és az alkalmazott mágneses tér közötti kölcsönhatásról: Alkalmazott mágneses térben az egyes atomok mágneses nyomatéka kvantálódik. A legegyszerűbb esetben csak két irányba igazodhat; vagy párhuzamosnak, vagy antiparalellnek kell lennie az alkalmazott mágneses mezővel. Ha egy atom mágneses momentuma párhuzamos a mágneses mezővel, a rendszer energiája kisebb, mint amikor az igazodás antiparalel. Az alkalmazott mágneses tér erőt gyakorol az egyes atomokhoz tartozó mágneses momentumokra. A rendszer energiája az alkalmazott mágneses tér nagyságától függ.
Ahelyett, hogy az adiabatikus demagnetizáció speciális esetére koncentrálnánk, vizsgáljuk meg az általánosított potenciál, \({\mathit{\Phi}}_{\theta }\), és annak általánosított elmozdulása, \(\theta\) változásához kapcsolódó energia- és entrópiaváltozásokat. (Adiabatikus demagnetizáció esetén \(\theta\) lenne az alkalmazott mágneses tér.) Ebben a rendszerben a reverzibilis változások leírásához három változóra van szükség. Az energiát és az entrópiát a hőmérséklet, a nyomás és az \(\theta\) függvényeként fejezhetjük ki:
\(E=E\left(T,P,\theta \right)\) és \(S=S\left(T,P,\theta \right)\). Az entrópia teljes differenciálegyenlete tartalmaz egy olyan kifejezést, amely az entrópia \(\theta\)-tól való függését határozza meg. Van
\
ahol \(C\left(T,P,\theta \right)\) írjuk, hogy hangsúlyozzuk, hogy jelen céljaink most azt igénylik, hogy állandó nyomáson és állandó \(\theta\) mellett mérjük a hőkapacitást.
Állandó nyomás, P, és állandó elmozdulás, \(\theta\) esetén az entrópia a hőmérséklettől a következőképpen függ
\
A posztulátum, hogy az entrópia bármely hőmérsékleten véges, azt jelenti, hogy a nyomás- és \(\(\theta\)-függő hőkapacitás abszolút nulla értéken nulla lesz. Vagyis abszolút nullponton a hőkapacitás eltűnik, függetlenül a P és \(\(\theta\) értékétől. Az érvelés pontosan ugyanaz, mint korábban. Korábban azt írtuk, hogy \(C_P\ balra(0\jobbra)=0\); a jelenlegi általánosított esetben \(C\ balra(0,P,\theta \jobbra)=0\).
Hasonlóképpen, abból a posztulátumból, hogy az entrópia a többi termodinamikai változó minden értéke esetén az abszolút nulla értéken állandóvá válik, az következik, hogy két tetszőleges \(P_1\) és \(P_2\) nyomás, valamint az általánosított elmozdulás két tetszőleges értéke esetén, \({\theta }_1\) és \({\theta }_2\),
\
és ebből következően
\ és \
Olyan folyamatot szeretnénk vizsgálni, amelyben egy rendszer a környezetében elérhető legalacsonyabb hőmérsékletről egy még alacsonyabb hőmérsékletre megy át. A végső hőmérséklet minimalizálása érdekében ezt a folyamatot adiabatikusan kell végrehajtani. Ez is egy lehetséges folyamat kell, hogy legyen, hogy \(dS\ge 0\). Az egyszerűség kedvéért tegyük fel, hogy ezt a folyamatot állandó nyomáson, \(P\) mellett végezzük, és a rendszer az \(P\), \(T_1\), \({\theta }_1\) által meghatározott állapotból az \(P\), \(T_2\), \({\theta }_2\) által meghatározott állapotba kerül, ahol \(T_1>T_2\). E két állapot entrópiája
\ és \
A folyamat entrópiaváltozása
\ \
Most tegyük fel, hogy a végső hőmérséklet nulla; azaz \(T_2=0\), tehát
\ Ebből következik, hogy \
ahol a jobb oldali egyenlőtlenség abból következik, hogy \(C\left(T,P,{\theta }_1\right)>0\). Ebből következik, hogy
\
ami ellentmond a harmadik törvény Lewis és Randall-féle állításának. Az a feltételezés, hogy a rendszer elérheti az abszolút nullpontot, a harmadik törvény Lewis és Randall-féle állításának ellentmondásához vezet. Ha tehát a Lewis és Randall-féle állítás igaz, akkor az abszolút nulla nem érhető el.
A fordítottja is érvényes, vagyis abból a tételből, hogy az abszolút nulla nem érhető el, megmutathatjuk, hogy a Lewis és Randall-féle állítás igaz. Ehhez átrendezzük a fenti \(\Delta S\) egyenletet,
\ \
Ha most feltételezzük, hogy a Lewis és Randall állítás hamis, akkor a jobb oldali kifejezés lehet kisebb vagy egyenlő nullával. A bal oldali integrál ekkor lehet nulla, ebben az esetben a rendszer elérheti az abszolút nullát. Ha a Lewis és Randall állítás hamis, akkor igaz, hogy a rendszer elérheti az abszolút nullát. Ezért: Ha a rendszer nem tudja elérni az abszolút nullát, akkor a Lewis és Randall állítás igaz.
A 7. és 8. ábra ezeket a gondolatokat a hőmérséklet-entrópia térben lévő kontúrdiagramokkal ábrázolja. Mindkét ábrán két kontúrvonal látható. Az egyik kontúrvonal a hőmérséklet- és entrópiaértékek olyan halmaza, amely mentén a nyomás \(P\) állandó, \(\theta\) pedig \({\theta }_1\) állandó. A másik kontúrvonal olyan hőmérséklet- és entrópiaértékek halmaza, amelyek mentén a nyomás állandó \(P\) és \(\theta\) állandó \({\theta }_2\). A kontúrvonal meredeksége
\
Mivel a hőkapacitás mindig pozitív, ez a meredekség mindig pozitív.
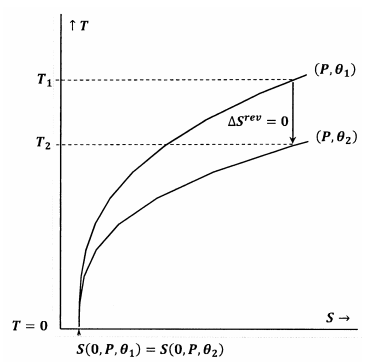
A 7. ábrán a Lewis és Randall-féle állítás teljesül. Amikor a hőmérséklet nullára megy, a kontúrvonalak az entrópia azonos értékénél találkoznak; ezek a kontúrok kielégítik az összefüggést
\
Az \(P\) és \({\theta }_1\) kontúrjából kiinduló adiabatikus (függőleges) út pozitív hőmérsékleten, \(T_2>0\) találkozik az \(P\) és \({\theta }_2\) kontúrjával. Mivel ez nyilvánvalóan igaz bármely \(P\) és bármely \({\theta }_2\) esetén, bármely adiabatikus folyamat végállapota \(T_2>0\) lesz. Mivel a Lewis és Randall-féle állítás teljesül, a rendszer nem érheti el az abszolút nullpontot, és fordítva.
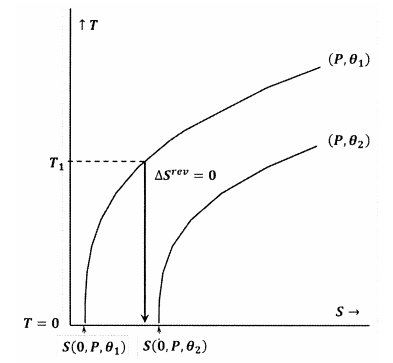
A 8. ábrán a Lewis és Randall-féle állítás sérül, mert \(S\left(0,P,{\theta }_1\right)\) \) van. Ebben az esetben egy elég alacsony kezdeti hőmérsékletről \(T_1\) indított adiabatikus folyamat anélkül éri el az abszolút nullpontot, hogy metszené az \(P\) és \({\theta }_2\) állandóra vonatkozó kontúrt. Mivel a Lewis és Randal-féle állítás sérül, a rendszer elérheti az abszolút nullpontot, és fordítva.