Az első bejegyzésben a 2D konvolúciókkal kezdtük, mert a számítógépes látás területén elért sikerek után a konvolúciók jelentős népszerűségre tettek szert. Mivel ezen a területen a feladatok képeket használnak bemenetként, és a természetes képek általában két térbeli dimenzióban (magasságban és szélességben) tartalmaznak mintázatokat, gyakrabban találkozunk példákkal 2D konvolúciókra, mint 1D és 3D konvolúciókra.
A közelmúltban azonban rengeteg siker született a konvolúciók természetes nyelvfeldolgozási feladatokban való alkalmazásában is. Mivel ezen a területen a feladatok szövegeket használnak bemenetként, és a szöveg egyetlen térbeli dimenzió (azaz az idő) mentén tartalmaz mintákat, az 1D konvolúciók nagyszerűen illeszkednek! A hagyományos rekurrens neurális hálózatok (RNN), például az LSTM-ek és a GRU-k hatékonyabb alternatívájaként használhatjuk őket. Az RNN-ekkel ellentétben ezek párhuzamosan is futtathatók az igazán gyors számításokhoz.
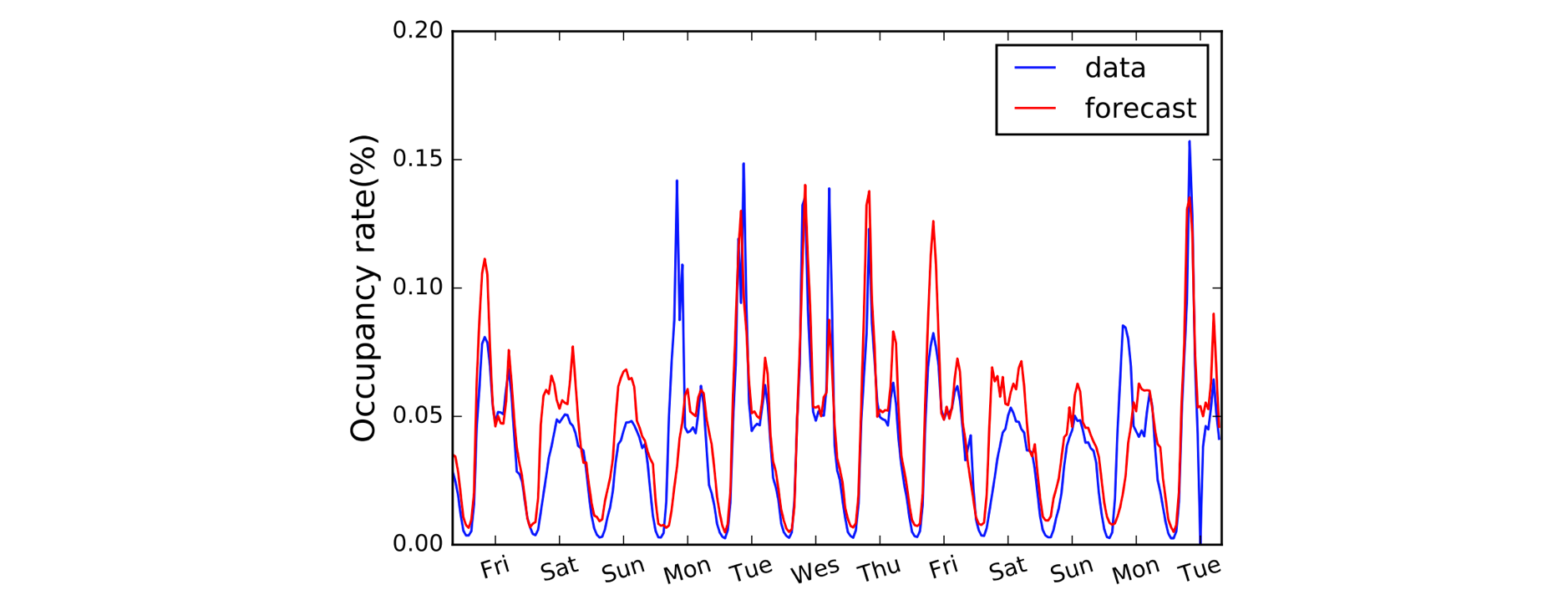
A másik terület, amely profitál az 1D konvolúciókból, az idősorok modellezése. Mint korábban, a bemeneti adatainknak egyetlen térbeli dimenziója van (azaz az idő), és időperiódusokon átívelő mintázatokat akarunk felvenni. Az ilyen típusú adatokat gyakran nevezzük “szekvenciálisnak”, mivel értékek sorozatának tekinthetők. A térbeli dimenziót pedig gyakran “időbeli” dimenziónak nevezzük. Az 1D konvolúciók használata az RNN-ek előtt szintén elég gyakori: az LSTNet modell egy példa erre, és a közlekedési előrejelzésre vonatkozó előrejelzései az alábbiakban láthatók.
A, B, C. Ez egyszerű, hiszen (1,3,3) pont (2,0,1) = 5.
Az elnevezési konvenciók tisztázása után nézzük most közelebbről az aritmetikát. Szerencsénk van, mert az 1D konvolúció valójában csak a 2D konvolúció egyszerűsített változata!

Az egyetlen kimeneti érték kiszámításán keresztül a 3-as méretű kernelünket alkalmazhatjuk a bemeneti mátrixunk bal oldalán lévő, ekvivalens méretű régióra. Kiszámítjuk a bemeneti régió és a kernel “pontproduktumát”, ami összefoglalóan nem más, mint az elemenkénti szorzat (azaz a színpárok szorzása), amelyet egy globális összeg követ, hogy egyetlen értéket kapjunk. Tehát ebben az esetben:
(1*2) + (3*0) + (3*1) = 5
A bemeneti tömb többi régiójára ugyanezt a műveletet (ugyanazzal a kernellel) alkalmazzuk, hogy megkapjuk a teljes (5,6,7,2) kimeneti tömböt; azaz a kernelt a teljes bemeneti tömbön átcsúsztatjuk. A 2D konvolúcióval ellentétben, ahol a kernelt két irányban csúsztatjuk, az 1D konvolúció esetében a kernelt csak egy irányban csúsztatjuk; ebben az ábrában balra/jobbra.
Felkészülés: Az 1D konvolúció nem ugyanaz, mint az 1×1 2D konvolúció.
A dolgok kódolása
Meglepő módon az 1D konvolúciónkhoz szükségünk lesz egy Conv1D blokkra a Gluonban. A kernel alakját 3-nak definiáljuk, és mivel ebben a példában csak egyetlen kernellel dolgozunk, megadjuk channels=1.
import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)
A bemenetünket most már átadhatjuk a conv blokkba egy előre definiált kernel segítségével.
input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>
Mi változik a padding, stride és dilation esetén?
A padding, stride és dilation hatását a 2D konvolúciókról szóló legutóbbi bejegyzésben láttuk, és ez nagyon hasonló az 1D konvolúciók esetében is. A paddinggal ezúttal csak egyetlen dimenzió (az időbeli dimenzió) mentén paddingolunk. A diagramunk az időt a vízszintes tengelyen keresztül ábrázolja, így a bemeneti adatoktól balra és jobbra (és nem felül és alul, mint a 2D konvolúciós példában) töltjük fel. A stride és a dilation esetében is csak az időbeli dimenzió mentén alkalmazzuk őket. Tehát egy példa kitöltéssel és stride-dal a következőképpen nézne ki:

A kódban két további argumentumot adunk hozzá: padding=1 és strides=2.
conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>
Előzetes: a bemeneti adatok méreteinek meg kell felelniük egy meghatározott sorrendnek, amelyet elrendezésnek nevezünk. Alapértelmezés szerint az 1D konvolúció az “NCW” formátumú bemeneti adatokra várja, azaz tételméret (N) * csatornák (C) * szélesség/idő (W). A 2D konvolúció esetében pedig az alapértelmezett formátum az NCHW, azaz kötegméret (N) * csatornák (C) * magasság (H) * szélesség (W). Nézze meg a
Conv1Dés aConv2D
layout argumentumát.