3D rekonstrukció

cd exercises/3d_reconstruction

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

Hogyan kell végrehajtani a gyakorlatot?

A gyakorlat elvégzéséhez meg kell szerkesztenie a MyAlgorithm.py fájlt, és be kell illesztenie bele a kódját, amely a két sztereónézetből rekonstruálja a 3d pontokat.

Hová kell beilleszteni a kódot?

A MyAlgorithm.py fájlba,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Az alkalmazás programozási felülete

• self.getImage('left') – a bal oldali kép
• self.getImage('right') – a jobb oldali kép
• self.point.PlotPoint(position, color) – a 3d eszközben a pont kirajzolása

Navigálás a GUI felületen

Eger alapú: Nyomva tartás és húzás a környezetben való mozgáshoz. Görgetés a nagyításhoz vagy kicsinyítéshez

Billentyűzet alapú: Nyílbillentyűk a környezetben való mozgáshoz. W és S billentyűk a nagyításhoz vagy kicsinyítéshez

elmélet

A számítógépes látásban és a számítógépes grafikában a 3D rekonstrukció egy objektum 3D profiljának meghatározása, valamint a profil bármely pontjának 3D koordinátájának ismerete. A rekonstrukció a következőképpen valósítható meg:

• Hardveralapú: A hardveralapú megközelítés megköveteli, hogy a rekonstrukciós feladatra specifikus hardvert használjuk. A strukturált fény, a lézeres távolságmérő, a mélységmérő és a radiometriai módszerek használata néhány példa.

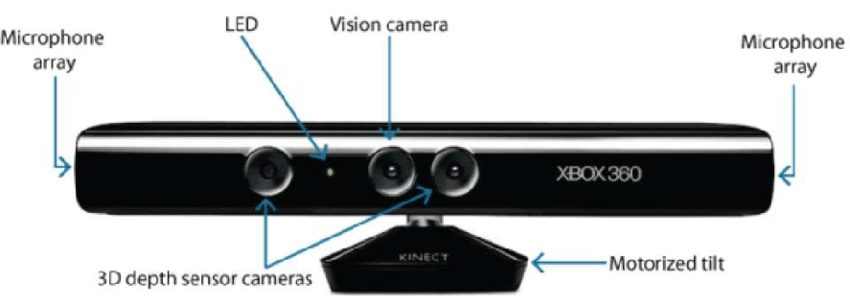
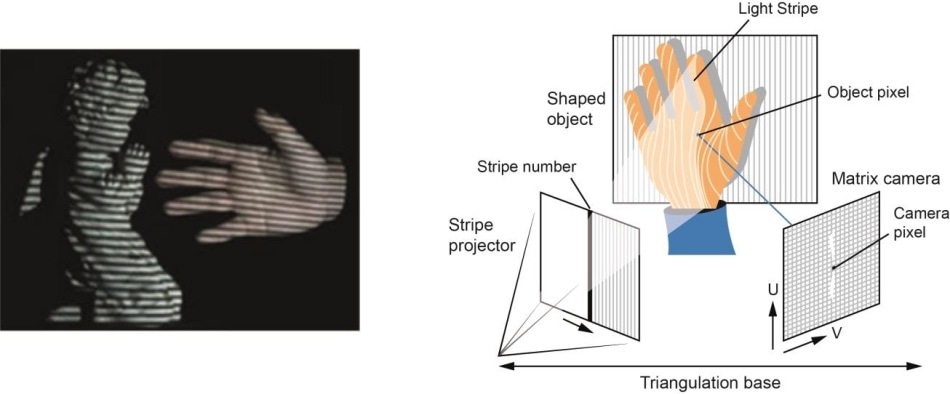
• Szoftver alapú: A szoftver alapú megközelítés a számítógép számítási képességeire támaszkodik a tárgy 3D tulajdonságainak meghatározásában. A Shape from shading, texture, stereo vision és homography néhány jó módszer.

Ebben a gyakorlatban a fő célunk a 3D rekonstrukció elvégzése szoftver alapú megközelítéssel, különösen a sztereo vision 3d rekonstrukcióval.

Epipoláris geometria

Ha két kamera két különböző pozícióból néz egy 3D jelenetet, számos geometriai kapcsolat van a 3D pontok és azok 2D képekre való vetítései között, amelyek a képpontok közötti korlátokhoz vezetnek. Ezeknek a tulajdonságoknak és korlátozásoknak a tanulmányozását epipoláris geometriának nevezzük. Az alábbi kép és magyarázat általánosíthatja a gondolatot:

Tegyük fel, hogy a 3d térben egy X pontot két nézetben, az elsőben x, a másodikban x' ponton képezünk le. Ha a sugarakat a képsíkokon keresztül visszavetítjük a kameraközpontjukra, akkor egy síkfelületet kapunk, amelyet π-vel jelölünk.

Tegyük fel most, hogy csak x ismerjük, akkor feltehetjük a kérdést, hogy a megfelelő x' pontot hogyan korlátozzuk. A π síkot az alapvonal(a kamera középpontjait összekötő vonal) és a x által meghatározott sugár határozza meg. A fentiekből tudjuk, hogy az ismeretlen x' pontnak megfelelő sugár a π-ben fekszik, tehát a x' pont a π és a második képsík l' metszésvonalán fekszik. Ezt az egyenest a x-nek megfelelő epipoláris egyenesnek nevezzük. Ez az összefüggés segít nekünk abban, hogy a jobb képen lévő pont keresési terét síkból egyenesre redukáljuk. Néhány fontos definíciót kell megjegyeznünk:

• Az epipólus a kamera középpontjait (az alapvonalat) a képsíkkal összekötő egyenes metszéspontja.

• Az epipólus sík az alapvonalat tartalmazó sík.

• Egy epipoláris vonal az epipoláris sík és a képsík metszéspontja.

Sztereo rekonstrukció

A sztereó rekonstrukció a fenti 3d rekonstrukció egy speciális esete, ahol a két képsík párhuzamos egymással és egyenlő távolságra van attól a 3d ponttól, amit ábrázolni szeretnénk.

Ebben az esetben a két képsík epipoláris vonala azonos, és párhuzamos a síkok szélességével, ami jobban leegyszerűsíti a megkötésünket.

3D rekonstrukciós algoritmus

A rekonstrukciós algoritmus 3 lépésből áll:

1. Egy képsíkban lévő jellemzőpontok felderítése
2. A fent találtnak megfelelő jellemzőpont felderítése
3. A pont háromszögelése a 3d térben

Nézzük meg őket egyenként

Ejlőpont felderítés

A jellemzőpont felderítés egy hatalmas terület, ahol már számos algoritmust tanulmányoztak. A Harris Corner Detection és a Shi-Tomasi algoritmusok sajátértékeket használnak a jó feature point megtalálásához. A probléma azonban az, hogy a 3D rekonstrukcióhoz sok pontra van szükségünk, és ezek az algoritmusok nem lesznek képesek ilyen nagyszámú jellemzőpontot biztosítani.

Ezért élpontokat használunk jellemzőpontként. Az algoritmus következő szakaszában kétértelműség lehet a felismerésükben. De a problémánkat megoldjuk azzal, hogy az éleket tekintjük jellemzőpontoknak. Az egyik igazán klassz élérzékelő a Canny Edge Detection Algorithm. Az algoritmus meglehetősen egyszerű és megbízható az élek generálása szempontjából.

Jellemzőpont-kivonatolás

Az epipoláris megkötés használata valóban leegyszerűsíti algoritmusunk időbonyolultságát. Általános 3d rekonstrukciós problémák esetén az egyik képkocka minden pontjához epipoláris vonalat kell generálnunk, majd ebben a mintatérben meg kell keresnünk a másik képkocka megfelelő pontját. Az epipoláris vonal generálása a mi esetünkben is nagyon egyszerű, ez csak a párhuzamos vonal iterpolációja a bal képből a jobb képsíkba.

A képek közötti megfelelés ellenőrzése számos algoritmust foglal magában, mint például a négyzetes különbségek összege vagy az energiaminimalizálás. Anélkül, hogy nagyon mélyre mennénk, egy egyszerű korrelációs szűrő használata is elegendő a mi felhasználási esetünkhöz.

Trianguláció

A trianguláció egyszerűbben fogalmazva nem más, mint a képsíkok két meghatározott pontja alapján kiszámítani, hogy a 3d pont hol fog elhelyezkedni.

A valóságban a képpontok helyzete nem mérhető pontosan. Az általános kamerák esetében geometriai vagy fizikai torzulások lehetnek. Ezért sok matematika áll e hiba minimalizálása és a legpontosabb 3d pontvetület kiszámítása mögött. Egy egyszerű modellhez lásd ezt a linket.

Súgók

Egyszerű tippeket adunk a 3d_rekonstrukciós feladat megoldásához. Az OpenCV könyvtárat széles körben használjuk ehhez a feladathoz.

Setup

A gyakorlat API-ját használva könnyen lekérdezhetjük a képeket. Továbbá a képek megszerzése után érdemes kétoldalú szűrést végezni a képeken, mert vannak olyan extra részletek, amelyeket nem kell figyelembe venni a 3d rekonstrukció során. Nézze meg az illusztrációkat a kétoldalú szűrés elvégzésének hatásairól.

Korrelációk kiszámítása

A OpenCV már rendelkezik beépített korrelációs szűrőkkel, amelyeket a matchTemplate() segítségével hívhatunk meg. Vigyázzunk az olyan szélsőséges esetekre, mint az élek és a sarkok.

Egy jó megfigyelés, hogy a bal oldali pontoknak a bal oldali részen, a jobb oldali pontoknak pedig a jobb oldali részen lesz megfelelés. Ezt a megfigyelést felhasználva könnyen felgyorsíthatjuk a megfelelés kiszámítását.

A pontok ábrázolása

A háromszögeléshez jól működik akár kézi, akár OpenCV alapú triangulatePoints függvény. Csak az algebrai megvalósítások végrehajtása során ügyeljünk az összes mátrix alakjára és méretére.

Ne feledkezzünk meg az egyszerű 3D koordináták és a homogén 4D koordináták közötti különbségről. Nézze meg ezt a videót a részletekért. Ha egyszerűen elosztjuk a teljes 4d vektort a 4. koordinátával, akkor megkapjuk a 3d koordinátákat.

A felhasználók változatos megvalósításai miatt előfordulhat, hogy a felhasználónak módosítania kell a háromszögelt pontok méretarányát és eltolását annak érdekében, hogy azok láthatóvá és ábrázolhatóvá váljanak a GUI felületen. A 3D koordináta vektor lekicsinyítése 500 és 1000 közötti értékkel jól működik. A 0 és 8 közötti eltolás is jól működik.

Illusztrációk