A PL eltávolítására szolgáló szubtrakciós eljárást először mintegy két évtizeddel ezelőtt dolgozták ki . Ez az eljárás nem érinti a PL frekvenciával szomszédos EKG-komponenseket. Ezt az elméleti tanulmányt a PL alapfrekvenciára végeztük, de a következtetések annak felharmonikusaira és következésképpen egy tetszőleges interferenciahullámformára is érvényesek. Az eljárás hatékonysága nem függ az interferencia amplitúdójától, amennyiben az erősítő nem telítődik. Ezenkívül az eljárás sikeresen megbirkózik az interferencia amplitúdójának és frekvenciájának változásaival. Az eljárást az évek során folyamatosan fejlesztették, és több ezer EKG-műszerben és számítógéppel támogatott rendszerben alkalmazták. Hasonló megközelítéseket más kutatók is publikáltak .
- Elvek
- Lineáris kritérium
- A PL amplitúdóváltozások kompenzálása
- Lineáris szűrés
- A PL frekvenciaingadozás kompenzálása
- Az eljárás hatékonyságának értékelése
- Az EMG zaj hatása
- Interferenciaelnyomás a nagy felbontású EKG-ban
- Elemmel táplált készülékek és számítógéppel segített EKG-rendszerek esete
- A névleges PL frekvenciához való automatikus igazítás
- Az eljárás elméleti fejlesztése
Elvek
A kivonási eljárást eredetileg f S mintavételi frekvenciával alkalmazzák, amelynek többszöröse, és hardveresen szinkronizált a PL f PL frekvenciával. Az eljárás a következő lépésekből áll :
-
A nullához közeli frekvenciasávú EKG szegmenseket egy megfelelő kritérium segítségével folyamatosan detektálják. Ezeket lineáris szegmenseknek nevezzük, és főként a PQ és TP intervallumokban, de az R és T hullámok kellően hosszú egyenes szakaszaiban is megtalálhatók.
-
Az ilyen szegmensek mintáit mozgó átlagolással, azaz egy lineáris fázisfésűs szűrőnek vetjük alá, amelynek első nulla értéke f PL . Így a szűrt minták nem tartalmaznak interferenciát.
-
Az interferencia amplitúdóit, az úgynevezett korrekciókat, a PL periódus, T PL , minden egyes fáziskapcsolt mintájára, n-re, úgy számítják ki, hogy a szűrt mintákat kivonják a szennyezett (eredeti) EKG-jel megfelelő mintáiból.
-
A kapott korrekciók halmazát a lineáris szakaszokban folyamatosan frissítik, a nem lineáris szakaszokban (általában a QRS-komplexumok és a nagy amplitúdójú T-hullámok körül) pedig arra használják, hogy az eredeti EKG-jelből kivonják az interferenciát.
A kivonási módszerrel kapott első eredmények egyike az 1. ábrán látható. Az interferenciát egy tiszta szimulált EKG-jelhez adtuk hozzá, hogy értékeljük a hibákat és a módszer hatékonyságát.
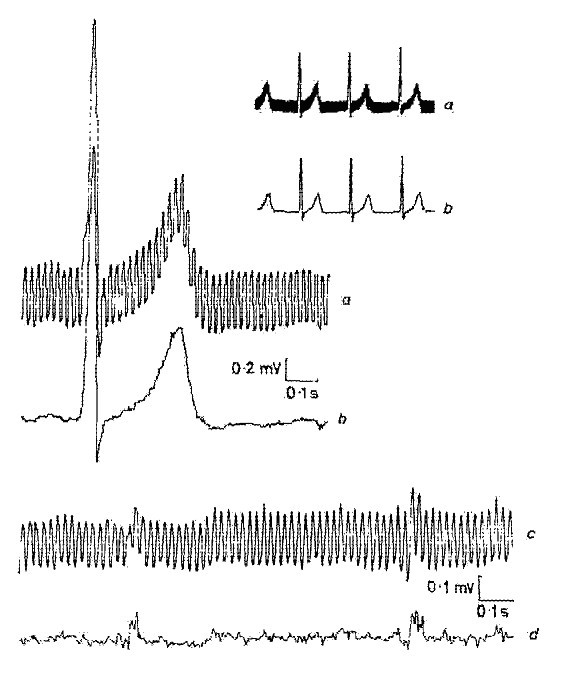
A kivonási eljárással kapott első eredmények egyike.
Lineáris kritérium
A lineáris kritérium, Cr, általában a jel második különbségének felel meg (a linearitás matematikai értékelése). Az első Cr-t a következő módon határozzuk meg. Hat egymást követő első különbséget, FD i , számolunk ki az egy T PL távolságra lévő X i jelmintákból :
FD i = X i+n – X i , mert i = 1 … 6 (1)
A PL interferencia az első különbségekben elnyomható, ha n = f S /f PL . Ebben az esetben n = 5, mivel az eljárást eredetileg f PL = 50 Hz és f S = 250 Hz névleges f PL-re fejlesztették ki. Továbbá a Cr meghatározásához a maximális FD max és a minimális FD min értékeket veszik alapul:
Cr = | FD max – FD min | <M, (2)
ahol M a küszöbérték.
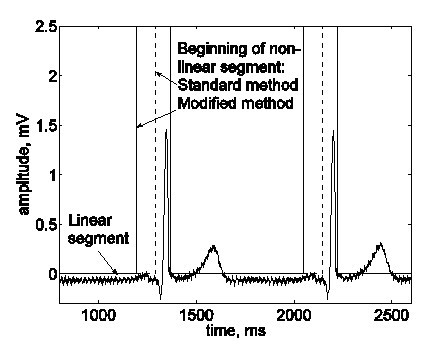
A 2. ábrán tipikus lineáris és nem lineáris szakaszok láthatók. A valós EKG-jelet (a nyomvonal) interferencia szuperponálja (b nyomvonal). A lineáris szegmensek alacsony frekvenciájú jelet és hálózati frekvenciájú komponenseket tartalmaznak. Az ilyen lineáris szegmensek közelítő frekvenciaspektruma a 3. ábrán látható.

Típusos lineáris és nemlineáris szegmensek a valós EKG-jelben.
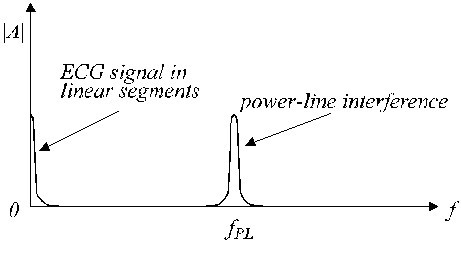
A lineáris szegmens közelítő frekvencia spektruma.
Ez a kritérium pontosan működik, de valós időben aligha alkalmazható, mert viszonylag lassú a megvalósítása. Ezt a hátrányt kiküszöböli Christov és Dotsinsky, akik egy módosított, mindössze két egymást követő különbségből álló kritériumot használnak.
Cr = | FDi+1- FD i | <M. (3)
Az első minta, amely nem teljesíti a (3) egyenletet, egy nem vonalas szegmens kezdetéhez kapcsolódik. A nemlineárisból lineárisba való átmenet során a (3) egyenletnek egymás után n-szer kell teljesülnie, hogy elkerüljük a lineáris szegmens idő előtti felismerését. A kritériumot valós időben f S = 400 Hz és n = 8 esetén valósították meg.
Később Dotsinsky és Daskalov a kritériumot két nem egymást követő különbségként definiálta:
Cr = |FDi+k- FD i | <M, for k >1 (4)
Ez a megközelítés pontosabbá teszi a lineárisból nemlineáris szegmensbe való átmenetet.
A PL amplitúdóváltozások kompenzálása
Minél gyakrabban frissítik a korrekciókat, annál jobban kompenzálják a PL amplitúdóváltozásait. Ezért a lineáris kritérium küszöbértékének, M-nek, ésszerűen kevésbé korlátozónak kell lennie, hogy az ideális lineáris jeltől eltérő néhány szegmens átlagolásával elkövetett hibák kisebbek legyenek, mint azok a hibák, amelyek akkor jelentkeznek, ha M a korrekció szórványos frissítését kezdeményezi. Kezdetben az M értéket 160 μV-ban határoztuk meg. Később heurisztikus értékeket találtak: M = 150 μV és M = 100 μV .
Lineáris szűrés
Páratlan n = 2m + 1 mintaszám esetén a PL-interferencia egy periódusában a szűrt érték:
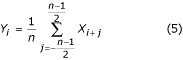
fázisban egybeesik a nem szűrt értékkel.
Páros n = 2m szám esetén a két érték a mintaperiódus felével fáziseltolódik:
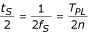
de a képlet
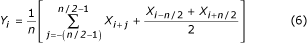
Az átlagoláshoz minden második, harmadik vagy q-edik minta vehető, ha n/q egész szám. Attól függően, hogy n/q páratlan vagy páros, a (7) vagy a (8) egyenletet használjuk.

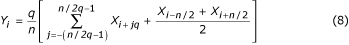
A maximális mintacsökkentés speciális esete merül fel q = n/2 esetén. A megfelelő képletet:
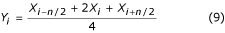
“hárompontos” szűrőnek nevezzük. A (8) egyenlet mellett a következő képlet
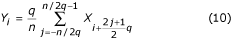
is alkalmazható, ha q páros. Abban az esetben, ha q = n/2, a szűrő “kétpontossá” válik, és a következőképpen ábrázolható:

A csökkentett mintaszám egy interferenciaperiódusban a fésűszűrő lebenyeinek fokozott meredekségét eredményezi, és lerövidíti a számítási időt. Ezeket az “előnyöket” azonban gondosan kell értékelni, hogy a nagy mennyiségű harmadik harmonikus jelenléte esetén ne sérüljön a Nyquist-szabály. A többi felharmonikus nem kerül figyelembe vételre, mivel a legmagasabb páratlan felharmonikusokat általában 100-150 Hz közötti határértékkel rendelkező aluláteresztő szűrőkkel elnyomják, míg a párosak gyakorlatilag hiányoznak a villamos erőművi generátorok pontos pólusgyártása miatt.
A PL frekvenciaingadozás kompenzálása
A névleges PL frekvenciától való megengedett eltérést egyes országokban a szabványok legfeljebb 1%-ra korlátozzák. A gyakorlatban az eltérés gyakran nagyobb. Kumaravel et al. 3%-os eltérésről számolt be. McManus et al. jelentős változásokat talált az interferenciafrekvenciában, amelyet a Common Standards for Electrocardiography (CSE) adatbázisból vett felvételekre szuperponáltak.
A frekvencia eltérések a nem többszörös mintavételezés speciális esetéhez vezetnek, ahol az egész szám helyett valós n van. Ez a bonyodalom megkerülhető, ha az eltéréseket az f PL folyamatos hardveres mérésével észleljük, és a t S mintavételi intervallumnak a névleges (R) érték körüli kis módosításával korrigáljuk, t RS = T RPL /n (itt T RPL = 20 ms a névleges T PL f RPL = 50 Hz esetén). Az f PL 49,5 és 50,1 Hz közötti eltérés esetén a t S eltérések 1%-os tartományban vannak, és következésképpen nem okoznak az automatikus EKG-osztályozáshoz általában használt paraméterek elfogadott mérési pontosságát meghaladó hibákat.
Az első megközelítés az S k (k = 1, 2…n) szekvenciák minden egyes első mintájának, S 1 -nek a T PL időszakokban történő triggerelését a PL feszültség tetszőlegesen választott, de állandó amplitúdójával társítja. A következő minták, S k (k = 2…n), t S időközönként következnek be, amelyet t S = T RTL /n értékkel kapunk. 50 Hz és n = 5 esetén t S = 4 ms. Az ezzel a megközelítéssel elkövetett hibák két típusát Dotsinsky és Daskalov tanulmányozta. Az első, a minták közötti szabálytalanságok miatt, f S = 400 Hz-nél elérheti az 1%-ot, f S = 250 Hz-nél pedig az 1,2%-ot, amennyiben az f RPL körül 1%-os eltérés van. A második típusú hiba nem haladja meg a 3%-ot, és a szűrt minta járulékosan eltolt helyének következménye.
Dotsinsky és Daskalov egy továbbfejlesztett megközelítésről számolt be. A folyamatban lévő T PL periódust mérik és elosztják n-nel. A kapott t S-t használják fel a következő T PL .
Az eljárás hatékonyságának értékelése
A szubtrakciós eljárás példáit a 4. és az 5. ábra mutatja. Az EKG-jelek az American Heart Association adatbázisából származnak. A jeleket a 60 Hz-es (PL-frekvencia az USA-ban) interferencia elnyomása érdekében notch-szűréssel szűrtük. Ezután a jeleket 50 Hz-es interferenciával keverjük, amplitúdójukat 0-tól 3,2 mVp-p-ig 200 μVs-1 sebességgel moduláljuk. A nyomvonalakat a következőképpen azonosítjuk: i) bemeneti jel; ii) szintetizált interferencia; iii) kevert jel; iv) feldolgozott jel; v) az eredeti és a feldolgozott jelek közötti különbség és vi) nagyított különbség. Valójában az elvetett komponensek közé tartoznak az elektromiográfiai (EMG) és egyéb zajok is. A jel egy nem elnyomott része, valamint az M-értékkel való kompromisszumból eredő kis maradék interferencia és torzítások is jelen vannak a különbségekben.
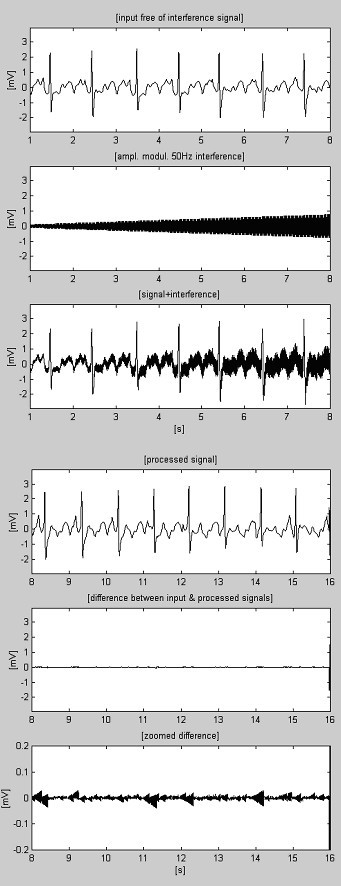
Feldolgozott AHA 3004d1 felvétel.
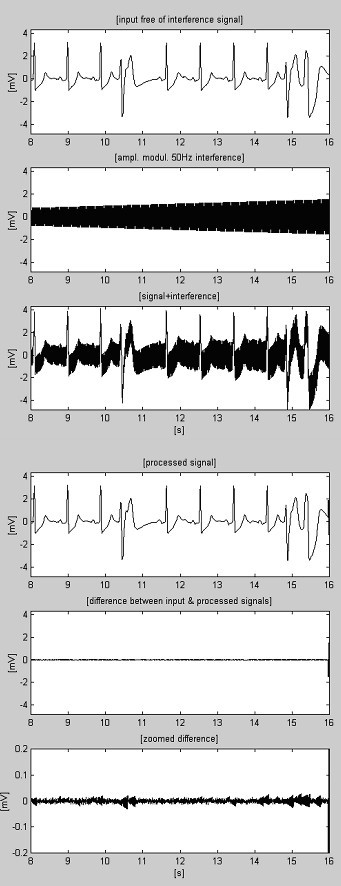
Feldolgozott AHA 6007d1 felvétel.
Két jelet használunk a kivonási eljárás hatékonyságának értékelésére csak az interferencia tekintetében. Az elsőt, amely a saját adatbázisunkból származik, feltételesen “tisztának” nevezzük (6. ábra). Az eredmény kis különbségeket mutat a bemeneti és a feldolgozott jelek között, ami szemmel láthatóan a bemeneti jelben megjelenő zajnak köszönhető. Ezt az eredményt a második szintetizált jellel ellenőrizzük, amely nem tartalmaz zavarokat (7. ábra). Amint látható, nincsenek torzítások. Ugyanezt a szintetizált jelet interferenciával szuperponáljuk és feldolgozzuk (8. ábra). Nem találunk maradék zavarást.
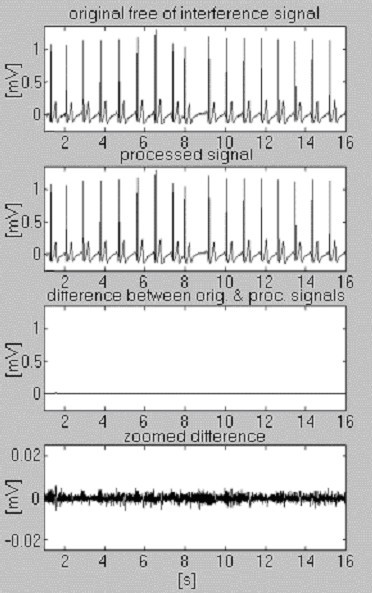
A feltételesen “tiszta” jel feldolgozása.
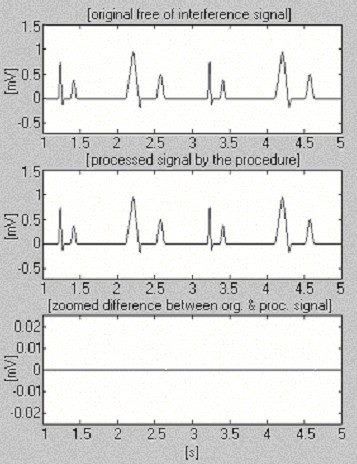
A szintetizált jel feldolgozása.
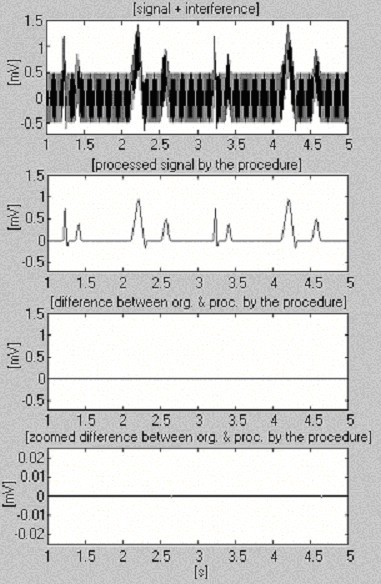
Feldolgozott szintetizált jel+interferencia.
Az EMG zaj hatása
Néha az EMG zaj olyan nagy, hogy a lineáris szegmens megtalálását akadályozza. Ennek következtében a pontatlan korrekciók, amelyek nem felelnek meg az interferencia amplitúdójának utolsó változásának, hibákat okoznak (lásd a 9. ábrán a 11. és 14. s közötti maradékzajt).
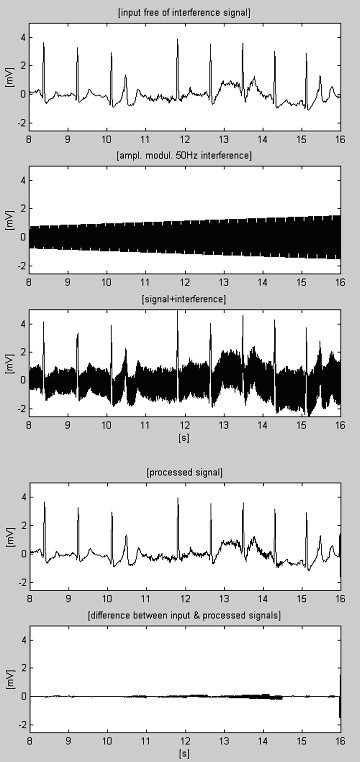
Feldolgozott EKG jel+EMG zaj+interferencia.
Egy nagyon egyszerű megközelítés az EMG zaj hatásának elnyomására az eljárás bevezet egy további párhuzamos puffert, ahol a jel folyamatban lévő részeit feltétel nélkül átlagolják . Ezt a puffert a linearitás pontos kimutatására használják. A 10. és a 11. ábra a párhuzamos puffer nélkül és a párhuzamos pufferrel kapott eredmények összehasonlítását mutatja. Az “a” nyomvonalak interferenciával és EMG-zajjal kevert EKG-jelet ábrázolnak. A 10. ábra “b” és a 11. ábra “c” nyomvonalai a lineáris és a nemlineáris szegmensek közötti átmeneteket (on-off függvények) jelzik. Amint látható, a 10. ábrán látható átlagolt jelrész nagyon korlátozott. Ennek következtében az eljárás hatékonysága csökken (10c. és 10d. ábra. Ezzel szemben a párhuzamos puffer lehetővé teszi a hosszú lineáris szegmensek detektálását (11c. ábra, és a feldolgozott jelben a maradék zaj (11d. ábra) alacsony. A zaj azonban nem nyomódik el teljesen, mert egy része részt vesz a korrekciós számításban.
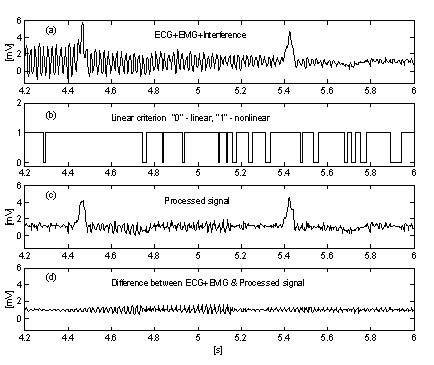
Párhuzamos puffer nélkül az interferencia+EMG zaj kivonása.
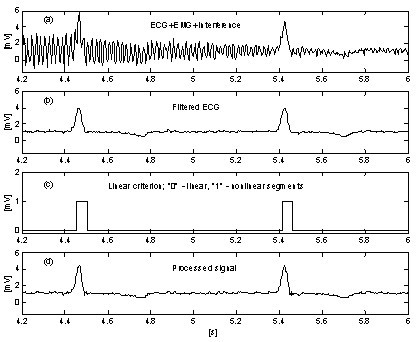
Az interferencia+EMG zaj kivonása párhuzamos pufferrel.
Az EMG-zaj elnyomásának további javulását Christov az M adaptív küszöbérték alkalmazásával érte el, amelyet az Rt zaj/jel arányhoz viszonyítva számítanak ki, amelyet a következőképpen határoznak meg: Rt = S NL /S F , ahol az S NL zajszint egyenlő a nemlineáris szegmensek összesített szélességével egy S F epochában, amely körülbelül megfelel a vizsgált RR intervallumnak. Az M = 150 μV kritériummal végzett linearitáskeresés a “tiszta” EKG (12a. ábra) és az azonos, de EMG-zajjal szennyezett jel (12b. ábra) esetében eltérő S NL értékeket mutat (12c. és 12d. ábra). A módszert MATLAB környezetben fejlesztettük ki. Az M kezdeti küszöbértéket 30 μV-nak választottuk. Ezután fokozatosan növeljük, amíg az Rt el nem éri a 10%-ot, majd elindítjuk a kivonási eljárást. Az Rt ≤ 0,1 értéket a “QRS-szélesség és RR-intervallumának aránya” sugallja, amely általában 10% körül van. Mind az interferencia, mind az EMG-zaj kiküszöbölése megfigyelhető a 13b. és 13d. ábrán, ahol M = 420 μV-ot használunk. Összehasonlításképpen a “tiszta” EKG-jelet M = 35 μV értékkel dolgoztuk fel (13a. és 13c. ábra).

Zajszintek SNL (c és d nyomvonal) a “tiszta” EKG-jel (a nyomvonal) és az EMG-vel szennyezett jel (b nyomvonal) esetében.
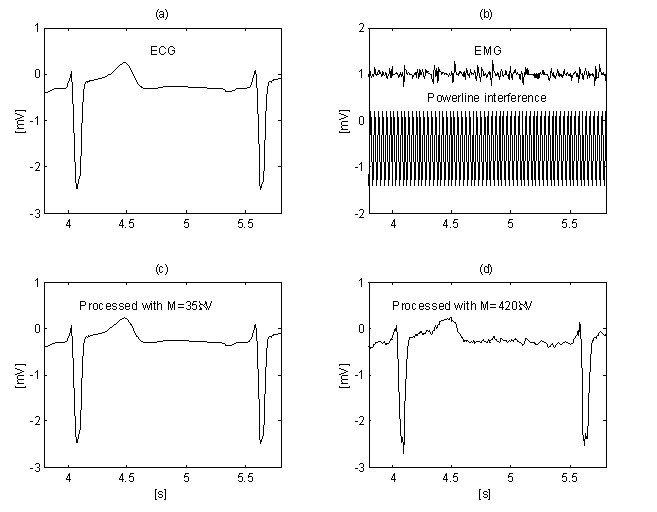
Interferencia+EMG zaj elnyomása adaptív M küszöbérték alkalmazásával: M = 35 μV értékkel feldolgozott “tiszta jel” (a) (c) és az eljárásnak alávetett szennyezett jel (b) M = 420 μV értékkel (d).
A pitvar- és kamrafibrillációban szenvedő betegeknél nem találhatók rendszeresen lineáris szegmensek. A hullámforma teljes megőrzése azonban nem szükséges a fibrilláció detektálásához, ezért mindenféle hagyományos szűrő alkalmazható.
Interferenciaelnyomás a nagy felbontású EKG-ban
A szubtrakciós eljárás nem alkalmazható közvetlenül a testfelszíni His-ECG-re, mivel az alacsony amplitúdójú és viszonylag alacsony frekvenciájú His-hullám nem különíthető el a lineáris szegmensekben. Így a His-hullámot a gyakorlatban elnyomják vagy akár el is távolítják a jelből. Az EMG-zaj általában nagyobb amplitúdójú és sokkal magasabb frekvenciatartalmú, mint a felszíni His-hullám. Ezért a küszöbérték, az M egyszerű megváltoztatása nem eredményezi a lineáris és nem lineáris szegmensek elfogadható elhatárolását.
Bazhina et al. a következő módosítást hajtotta végre. Az észlelt nemlineáris szegmens kezdetét a QRS-komplexus előtt 100 ms-t balra tolják, így a His-hullám régiót alapértelmezés szerint nemlineáris szegmensként definiálják (14. ábra).
A QRS-komplexust tartalmazó nemlineáris szegmens kezdetét alapértelmezés szerint 100 ms-t balra tolta el, hogy magában foglalja azt a zónát, ahol a His-köteg hullám várhatóan megjelenik.
A kivonási eljárást és három másik módszert: a notch-szűrőket, a spektrális interpolációt és a regressziós kivonást az eredeti jel minimális torzításával teszteltük. A szubtrakciós és a regressziós-szubtrakciós eljárás bizonyult a legjobbnak, mivel Baratta és társai hasonló koncepciót alkalmaznak a lineáris szegmensek zajbecslésére. A regresszió-szubtrakció rosszul kezeli az interferencia amplitúdóváltozásait az aktuális szegmensen belül.
Elemmel táplált készülékek és számítógéppel segített EKG-rendszerek esete
Az f PL hardveres mérése , amely az interferencia frekvenciamodulációjának kompenzálásához szükséges, nem valósítható meg az elemmel táplált készülékekben és néhány számítógéppel segített EKG-rendszerben. Dotsinsky és Stoyanov tanulmányozta az állandó amplitúdójú interferencia frekvenciaváltozásainak azt a tartományát, amelynél a reziduális rész szinkronizált mintavételezés alkalmazása nélkül is elfogadható szintre korlátozódik. Azt találták, hogy 20 μVp-p alatti maradék interferencia érhető el az eljárással: i) interferencia amplitúdó ≤ 0,4 mVp-p és ii) ≤ 0,0125 Hzs-1 frekvenciaváltozással. Mivel a tápegységgel szemben támasztott ilyen követelmények gyakran túlléphetők, kifejlesztettek egy szoftveres interferenciamérést.
Az EKG jelet kezdetben egy 49-51 Hz-es sávszűrővel dolgozzák fel. Az interferencia pozitív irányú meredekségéből vett két szomszédos minta, a Br L és a Br R , amplitúdóját a nulla vonal alatt és fölött helyezkedik el, megmérjük (15. ábra). A CP keresztezési pont és a jobb oldali minta, Br R , közötti távolságot, t CP , folyamatosan kiszámítjuk a következők szerint:
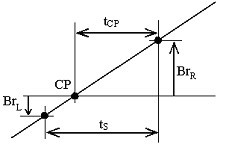
Interferencia zérusátmenet.

T PL változása esetén a t S újradefiniálása

Ezt a megközelítést MATLAB környezetben valósítottuk meg. Az f S = 500 Hz és f RPL = 50 Hz mintavételi frekvencia esetén az n értéke 10. A kn szorzat határozza meg az új tCP,i + kn az előző tCP,i kiszámítása és helyettesítése előtt ajánlott időt. A 16. ábra egy feldolgozott 1 mV-os EKG-jelet mutat, miután interferenciával keverték, 2 mVp-p állandó amplitúdóval és rendkívül gyorsan, 8 s frekvenciánként 1 Hz-cel változóval (első nyomvonal). A kapott hatékonyság értékeléséhez a szinkronizált mintavételezés nélküli, nagyított különbség (utolsó nyomvonal) is látható.
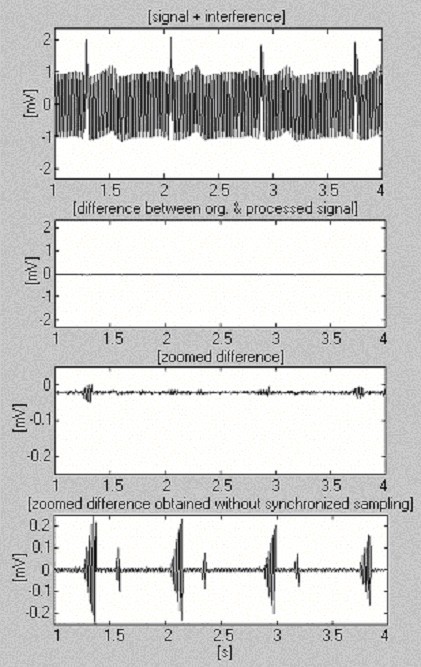
Szoftveres hálózati frekvenciaméréssel végzett kivonási eljárás.
A következő logikai lépés a következő: i) az EKG műszer névleges t S értékének megtartása, ii) a jel újramintázása a folyamatban lévő mért f PL szerint az interferencia megszüntetése érdekében és iii) visszatérés a névleges t S értékhez. Az ilyen megközelítés első eredményei nagyon ígéretesek. Így a változó f PL szoftveres kompenzálása, valamint a kivonási eljárás teljes megvalósítása egy műszerben, beleértve az 50 vagy 60 Hz-es f RPL automatikus beállítását, a hardveráramköröktől és a megfelelő szoftvertől függetlenül megvalósul.
A névleges PL frekvenciához való automatikus igazítás
Az 50 és 60 Hz-es környezetben végzett alternatív interferencia kivonás közös programja nem többszörös mintavételezéshez, azaz valós n-hez vezet. A t S széles körben használt értékei f RPL = 50 Hz esetén, például 250, 500 és 1000 Hz, a 4,1(6), 8,3(3) és 4,1(6) irracionális n-nek felelnek meg, ha 60 Hz-es interferenciát kell kiküszöbölni. Fordított esetben f S = 360 Hz esetén n = 7,2 szükséges. Az n* kerekített értékek használata nem elfogadható, mivel jelentős hibát eredményeznének.
Egy nagyon egyszerű, f S változást nem igénylő megoldást talált Dotsinsky és Sztojanov . Az eredeti eljárás az interferencia egy periódusára, T PL , fésűs szűrőt alkalmaz. Így a program gyorsabban fut. Általában n-t k > 1 teljes periódusból lehet venni. Az eljárás akkor működik, ha:
n = kT PL /t S egész szám.
t S = 2 ms (f S = 500 Hz) és f RPL = 50 Hz esetén a (14) egyenletet kielégítő k legkisebb értéke valóban k = 1. 60 Hz esetén azonban k egyenlő 3-mal. A 20 és 40 Hz-es szubharmonikusokhoz tartozó nullák is megjelennek, de ezek nem befolyásolják az eljárást. Ezért elég, ha az n értéket 10 (k = 1) és 25 (k = 3) között változtatjuk, hogy mindkét interferenciával dolgozhassunk. Ebből a célból két digitális sávszűrő ellenőrzi a bejövő jelet. A 17. ábrán látható, hogy az interferenciával átfedő frekvenciasávú szűrő egy nagyságrenddel nagyobb kimeneti jelet generál, mint a másik szűrő.
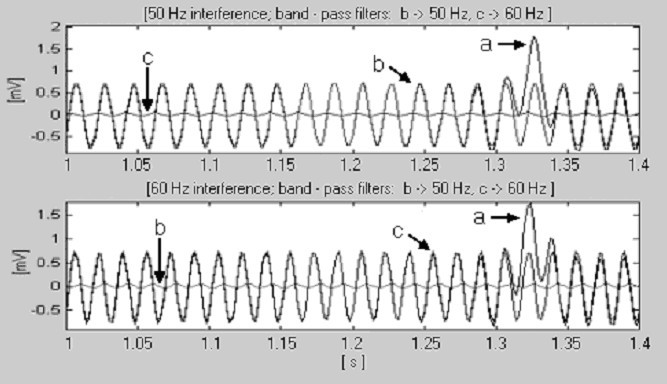
A névleges hálózati frekvencia kimutatása, a) a QRS komplex egy része, b) 50 Hz-es interferencia és c) 60 Hz-es interferencia.
Az eljárás elméleti fejlesztése
A szubtrakciós eljárás elméletét Mihov , Levkov és Mihov , valamint Mihov et al. fejlesztették tovább. Négyféle szűrőt javasoltak, olyan általánosított struktúrában megvalósítva, amely a nem többszörös mintavételezés szinte minden esetére, beleértve az interferenciafrekvencia-változásokat is, szinkronizált AD konverzió alkalmazása nélkül megoldhatja a problémákat.
A többszörös mintavételezésben az úgynevezett D-szűrőt úgy határozzák meg, mint a Cr a (2) egyenletben, ahol a második különbséget, D i , egy T PL távolságban lévő FD s-ekkel kapjuk:
D i = (X i+n – X i ) – (X i – X i-n ) = X i-n – 2X i + X i+n (15)
A D-szűrő átviteli függvényének nullpontjai f = 0 és f = f PL Hz-nél vannak, ami az ábrán 50 Hz-nek felel meg. 18.

A D-szűrő átviteli függvénye fPL = 50 Hz esetén.
A K-szűrő az (5) és (6) egyenletekkel bemutatott mozgó átlagot írja le. Átviteli függvénye páratlan sokaság esetén n = 5 esetén a 19. ábrán látható.
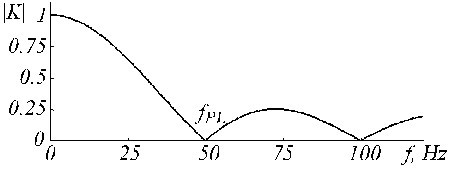
K-szűrő átviteli függvénye fPL = 50 Hz és n = 5 esetén.
Az interferenciakomponensek folyamatos számításához használt egyenlet:
B i = X i – Y i (16)
ténylegesen egy (1-K)-szűrőnek nevezett digitális szűrőt határoz meg.
Ezeken túlmenően a szűrőket nem többszörös mintavételezés esetén újra definiáljuk, és f S = 250 Hz-et f RPL = 60 Hz mellett vesszük figyelembe a szoftverfejlesztés szemléltetésére.
Az átviteli függvény nulláinak megőrzése érdekében a D-szűrőt egy korrekciós szűrővel kell kivonni, amelynek f = 0-nál nullája van, és a D RPL erősítése f = f RPL-nél megegyezik a D-szűrő erősítésével ugyanarra a frekvenciára, f RPL-re. A korrekciós szűrő szintézise egy hárompontos segédszűrőn alapul, amelyet a következő egyenlet ad meg:

ahol (n/2)* az n/2 kerekített értéke.
Mivel A RPL a segédszűrő erősítése f = f RPL esetén, a korrekciós szűrőt meg kell szorozni a D RPL /A RPL aránnyal. A megfelelő átviteli függvények felhasználásával a D RPL és az A RPL előre kiszámítható:
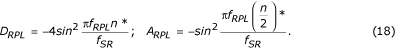
Végül a korrigált D*-szűrő a következő

és a 20. ábrán a “c” nyomvonal mutatja, ahol az “a” és a “b” nyomvonal a D-szűrő, illetve a korrekciós szűrő.
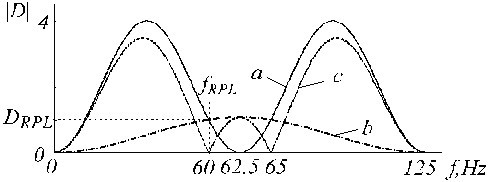
Az a) D-szűrő, a b) segédkorrekciós szűrő és a c) korrigált D-szűrő átviteli függvényei.
A K-szűrő átviteli függvényének f = f RPL esetén nullát, f = 0 esetén egységnyi erősítést és lineáris fázisválaszt kell megőriznie. A K-szűrő korrekciójának eljárása hasonló az előzőhöz. A segédszűrőt a korrekciók számításához használt képlet adja:
A i = X i – Y i , (20)
A szűrő erősítése egyenlő 1 – K RPL f = f RPL esetén, ahol K RPL a K-szűrő erősítése ugyanarra az f RPL frekvenciára. A segédszűrőt megszorozzuk K RPL /(1 – K RPL ) értékkel, és kivonjuk a K-szűrőből. A korrigált K*-szűrő egyenlete:
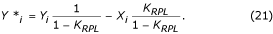
A K RPL konstans becsülhető:

a páratlan, illetve páros sokszorosság esetén.
Egy példa a K-szűrő korrekciójára a 21. ábrán látható, ahol az “a”, “b” és “c” nyomvonalak az elsődleges K-szűrőt, a segédszűrőt és a korrigált K*-szűrőt ábrázolják.
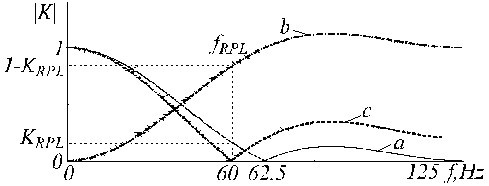
Az a) K-szűrő, a b) segédkorrekciós szűrő és a c) korrigált K-szűrő átviteli függvénye.
Nem többszörös mintavételezés esetén fáziskülönbség jelentkezik a folyamatban lévő EKG-minták és az általában egy ideiglenes FIFO-pufferben (first-in-first-out) elhelyezett B i zavaró komponensek (16. egyenlet) között. Ezért a B i-t módosítani kell, mivel a nem lineáris szegmensek során kivonják az EKG-mintákból. A kompenzációs eljárás viszonylag bonyolult. A 22. ábra az ideiglenes puffer tartalmát mutatja. Az aktuális interferencia minta, B i-n *, nem esik egybe a visszaállított mintával, B i . Amplitúdóját újra kell számítani a kettő közötti fáziskülönbség kompenzálása érdekében. Ezt egy új, lineáris fázisválaszú és f = f RPL esetén egységnyi erősítésű, B-szűrőnek nevezett szűrővel lehet elvégezni. Ezt az ismert K-szűrőből szintetizáljuk, az interferencia-periódusnak megfelelő ablakkal. Páratlan n* esetén a következőképpen írható le:
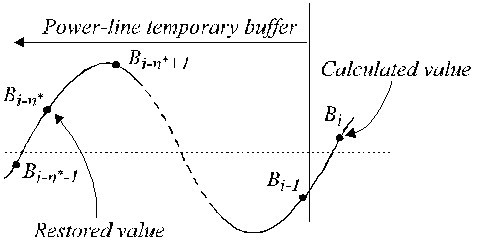
Az ideiglenes pufferben visszaállított értékek.
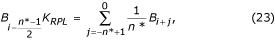
ahol K RPL az átlagoló szűrő interferenciájának a (22. egyenlet által megadott erősítése.)
A visszaállított B i pufferérték a következőképpen számítható:
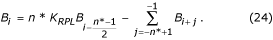
Páros n* esetén:
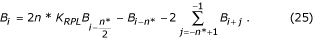
A B-szűrő átviteli függvénye az ábrán látható. 23.
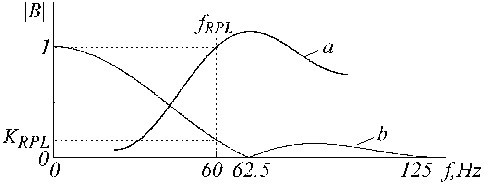
Az a) B-szűrő és b) az ismert K-szűrő átviteli függvényei.
Az általánosított szerkezetet az ábra mutatja. 24. ábra, ahol a kivonási eljárás moduljai a következők:
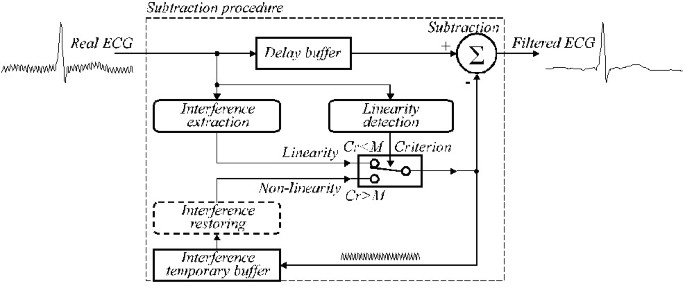
A kivonási eljárás általánosított szerkezete.
-
Linearitásérzékelés. D-szűrőt alkalmazunk az egyes jelminták szomszédságának linearitásának értékelésére.
-
Interferencia-kivonás. (1-K)-szűrőt alkalmazunk az interferencia komponens kiszámítására.
-
Kritérium. A Cr <M feltétel a kivont vagy helyreállított PL interferenciát küldi a Subtraction.
-
Interferencia ideiglenes pufferbe. A nemlineáris szegmensben korrekcióként használt extrahált vagy visszaállított interferencia komponens a hálózati interferencia folyamatban lévő fázisával zárolt pozícióban kerül elmentésre.
-
Interferencia visszaállítás. A B-szűrőt nem többszörös mintavételezés esetén hívja meg a nemlineáris szegmensekben a bemeneti jelmintákból kivonandó valódi korrekciós értékek visszaállítása érdekében.
-
Késleltetési puffer. Kompenzálja a késleltetést, amely a D-szűrő és az (1-K)-szűrő esetén jelentkezik, és elengedhetetlen, ha az eljárás kvázi valós időben fut. Ellenkező esetben a puffer figyelmen kívül hagyható.
-
Subtrakció. A kivont vagy helyreállított interferenciaértéket kivonjuk a késleltetett bemeneti jelből, hogy “tiszta” EKG-jelet adjunk ki. Nemlinearitás esetén mind az interferencia kivonása, mind a kivonás K-szűrőt alkalmaz.
Az általánosított struktúrának megfelelő továbbfejlesztett algoritmust off-line teszteltük. Az eredményeket f S = 250 Hz és f RPL = 60 Hz esetén a 25. ábra mutatja.
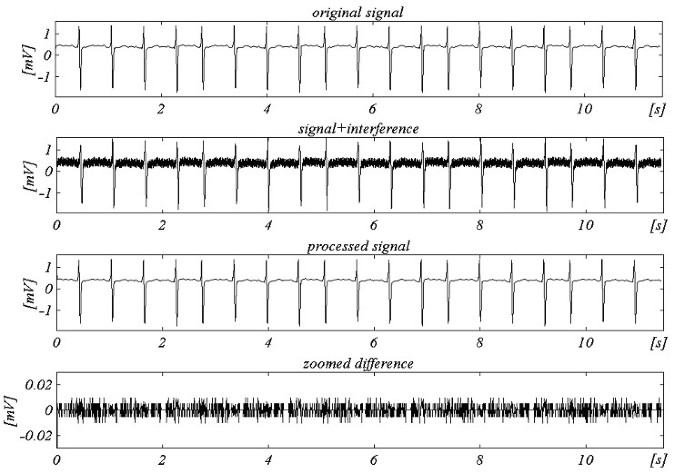
Példa nem többszörös mintavételezésre fRPL = 60 Hz és fS = 250 Hz esetén.