Az Abel-csoport olyan csoport, amelynek elemei ingadoznak (azaz 
minden elemre 
és 
). Az abéliumi csoportok tehát szimmetrikus szorzótáblájú csoportoknak felelnek meg.
Minden ciklikus csoport abéliumi, de egy abéliumi csoport nem feltétlenül ciklikus. Egy abéli csoport minden alcsoportja normális. Egy Abel-csoportban minden elem önmagában egy konjugációs osztályba tartozik, és a karaktertáblában egyetlen elem, az úgynevezett csoportgenerátor hatványai szerepelnek.
A Wolfram Nyelvben az AbelianGroup függvény a 
, 
, ….
fokozatú ciklikus csoportok egyenes szorzatát jelenti.
Nem ismert általános formula egy adott csoportrendű nem izomorf véges csoportok számának megadására. Azonban a 
adott 
csoportsorrendű nem izomorf abéliumi véges csoportok száma 
írásával
 |
(1)
|
ahol a 
különböző prímtényezők, akkor
 |
(2)
|
ahol 
a partíciós függvény, amely a Wolfram Language-ben FiniteAbelianGroupCount néven van implementálva. A 
értékei 
, 2, … esetén 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 3, 2, …. (OEIS A000688).
A legkisebb rendek, amelyekre 
, 2, 3, … nem izomorf Abel-csoportok léteznek: 1, 4, 8, 36, 16, 72, 32, 900, 216, 144, 64, 1800, 0, 288, 128, …. (OEIS A046056), ahol 0 a nem izomorfikus Abel-csoportok lehetetlen számát (azaz nem partíciószámok szorzatát) jelöli. A “hiányzó” értékek a következők: 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41, 43, 46, … (OEIS A046064). Az Abel-csoportok növekményes legnagyobb számai a rend függvényében: 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, … (OEIS A046054), amelyek az 1, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, … rendek esetében fordulnak elő. (OEIS A046055).
A Kronecker-féle dekompozíciós tétel kimondja, hogy minden véges Abel-csoport felírható prímteljesítményű csoportrendű ciklikus csoportok közvetlen csoportproduktumaként. Ha egy véges csoport csoportrendje 
prím, akkor létezik egyetlen 
rendű Abel-csoport (jelölve 
) és nincs nem Abel-csoport. Ha a csoport rendje egy prím négyzete 
, akkor két Abel-csoport létezik (jelölve 
és 
. Ha a csoportsorrend egy 
köbös prím, akkor három Abel-csoport van (jelölve 
, 
és 
), és összesen öt csoport. Ha a rend két prímszám 
és 
szorzata, akkor pontosan egy 
csoportrendű Abel-csoport létezik (jelölve 
).
Egy másik érdekes eredmény az, hogy ha 
a 
csoportrendű nem izomorf Abel-csoportok számát jelöli, akkor
 |
(3)
|
ahol 
a Riemann-zétafüggvény.
A 
rendű Abel-csoportok számai: 1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15, 17, 18, 19, 20, 25, … (OEIS A063966) a 
, 2, …. esetében. Srinivasan (1973) azt is kimutatta, hogy
 |
(4)
|
hol
 |
 |
 |
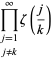(5)
|
 |
 |
 |
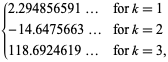(6)
|
(OEIS A021002, A084892 és A084893) és 
ismét a Riemann-zétafüggvény. Megjegyezzük, hogy Richert (1952) tévesen adta meg 
. Az összegek 
felírhatók az explicit formákban is
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
 |
 |
 |
(9)
|
DeKoninck és Ivic (1980) megmutatták, hogy
 |
(10)
|
hol
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A084911) a prímek feletti 
szorzat és 
ismét a partíciós függvény.
A nem izomorf nem Abel-csoportok számának határértékeit Neumann (1969) és Pyber (1993) adja meg.
Az Abel-csoportokkal kapcsolatban számos matematikai vicc létezik (Renteln és Dundes 2005):
K: Mi a lila és kommutál? V: Egy Abel-szőlő.
K: Mi a levendula és ingadozik? V: Egy abeli félszőlő.
K: Mi az, ami lila, ingázik, és korlátozott számú ember imádja? V: Egy véges számú Abel-szőlő.
K: Mi tápláló és ingázik? V: Egy abéli leves.