- Introduction
- Anyagok és módszerek
- Anyag
- A résztvevők
- Műveletek
- Nemlineáris regresszióelemzés
- Eredmények és megbeszélés
- Kísérleti eredmények leírása
- Az emberi hüvelykujj-indexujj maximális megragadó tömegét befolyásoló tényezők
- Az emberi hüvelykujj-indexujj maximális megragadási átmérőjét befolyásoló tényezők
- Diszkusszió
- Következtetés
- Adatok hozzáférhetőségi nyilatkozata
- A szerzők hozzájárulása
- Finanszírozás
- érdekellentét
Introduction
A többujjas ügyes kezekkel összehasonlítva a kétujjas bionikus kéz egyszerű mechanikai szerkezettel rendelkezik és könnyen tervezhető a mozgás, ezért mindig használják a gyümölcsszüretelő robotokban (Bac et al., 2017; Silwal et al., 2017). A gyümölcsszüretelő robotok munkakörnyezete azonban rendkívül összetett, például a növényben lévő gyümölcsök mérete, alakja, testtartása és helyzete eltérő (Li et al., 2019a, b), és a meglévő kétujjas bionikus kezek nehezen felelnek meg a gyümölcsszüretelés megragadási követelményeinek (Li et al., 2013), ezért a robotokat eddig még nem használták gyakorlati gyümölcsszüretelésre. Az agy és a szem koordinációjának segítségével az egyének mindig megbízható teljesítményűnek tekinthetők, ha képesek a célzott gyümölcs megragadásának, mozgatásának és elengedésének feladatait csak a hüvelyk- és mutatóujj segítségével elvégezni, és ennek a stabil manipulációs rendszernek az általános teljesítménye ésszerű. Az emberi kéz egy erős, többfunkciós eszköz, és képességeinek feltárása segíti a kutatókat abban, hogy meghatározzák egy bionikus robotkéz ésszerű fogási tömegét és méretét, azzal a szándékkal, hogy megismételjék a képességeit (Feix et al., 2014; Chen et al., 2019). Ergonómiai szempontból a gyümölcsszüretelő robotok tervezőinek meg kell érteniük az emberi hüvelykujj-indexujj kooperatív megragadási képességeit, valamint az ujjhossz és a megragadási képességek közötti mennyiségi korrelációt az újonnan tervezett kétujjas bionikus kezek esetében, hogy javítsák megragadási teljesítményüket (Yussof és Ohka, 2012; Wang és Ahn, 2017).
Az emberi hüvelykujj-indexujj megragadási viselkedését kiemelő tanulmányok az elmúlt évtizedben jelentek meg. Egyes kutatók kimutatták, hogy a manipuláció során a megragadás stabilitását elsősorban a tárgy súlya, az ujjhegyek és a tárgyfelület közötti relatív görbület és súrlódási erő, valamint a két érintkezési pont közötti távolság befolyásolja, amikor egy tárgyat a hüvelykujj-indexujj megszorított (Li et al., 2013; Luciw et al., 2014). Biegstraaten és munkatársai (2006) arra a következtetésre jutottak, hogy a nyúlási és emelési mozgások meglehetősen függetlenek voltak, amikor egy tárgyat precíziós fogással fogtak meg (Biegstraaten és munkatársai, 2006). Vigouroux és munkatársai (2011) azt javasolták, hogy amikor az emberi hüvelykujj-indexujj különböző szélességű tárgyakat fogott meg, akkor az ujjízületi testtartások, az izomerő és a fogóerő jelentősen változott a tárgy szélességének függvényében, és érdekes eredmény volt, hogy a nagy hajlítóizmok izomerő/fogóerő aránya különösen stabil maradt a szélesség függvényében, míg a többi izom aránya nagymértékben különbözött. Ezenkívül különböző kutatásokat végeztek az emberi ötujjas megragadási képességekkel kapcsolatban is (Vigouroux et al., 2011). Eksioglu (2004) kimutatta, hogy az egyén kézantropometriájához viszonyított optimális fogástávolság körülbelül 2 cm-rel rövidebb, mint a módosított hüvelykujj-körfogás hossza a maximális akaratlagos izometriás fogóerő, az izomaktivitás és a szubjektív értékelés megítélési kritériumai alapján. Seo és Armstrong (2008) bemutatta, hogy amikor hengeres fogantyúkat fogtak meg erőteljes fogástartásban, a fogantyú átmérőjének és a kézhossznak az aránya a fogóerő, a normál erő és az érintkezési felület eltéréseinek 62%-át, 57%-át és 71%-át magyarázza, Seo és Armstrong (2008). Li és munkatársai (2010) azt várták, hogy több antropometriai paraméter közül, mint például a magasság, a testsúly, a csukló és az alkar, a kéz és a tenyér hossza, a kézkerületnek van a legerősebb korrelációja a maximális fogóerővel. Bansode és munkatársai (2014) kimutatták, hogy a domináns kéz fogóereje férfiaknál és nőknél szignifikáns pozitív korrelációt mutatott az életkorral, a magassággal, a testtömeggel és a testtömegindexszel, valamint a domináns kéz kiterjedésével, míg a derékkörfogat és a derék-csípő arányával nem mutatott egyértelmű összefüggést. Feix és munkatársai (2014) megállapították, hogy az emberi kéz optimális megragadási képessége a tömeget tekintve kevesebb, mint 500 g, a tárgy szélessége pedig a megragadás helyén kevesebb, mint 7 cm.
Összefoglalva, jelentős előrelépés történt ezen a területen. Mindazonáltal kevesebb figyelmet fordítottak az emberi hüvelyk- és mutatóujj kooperatív megragadási képességére és az azt befolyásoló tényezőkre. Ez azt jelenti, hogy az emberi kéz képességét leutánozni szándékozó robotkezek ergonómiai tervezésénél technikai hiányosság van. Ezért a meglévő szakirodalmi adatok alapján vizsgálatokat végeztünk annak érdekében, hogy megvizsgáljuk az emberi test jellemzőinek hatását (pl, életkor, nem, termet, használt kéz, hüvelyk- és mutatóujj hosszának összege és a mutatóujj és hüvelykujj hosszának aránya) a hüvelyk- és mutatóujj fogási képességére, nevezetesen a maximális fogási tömegre és a hüvelyk- és mutatóujj átmérőjére, többszörös nemlineáris regresszióelemzés módszerével.
Anyagok és módszerek
Anyag
Az emberi hüvelykujj-indexujj kooperatív megragadási képességeinek vizsgálatára 2017 augusztusában 20 különböző tömegű tömör henger és 15 különböző külső átmérőjű gyűrű készült megragadandó tárgyként. A 40 mm dc átmérőjű tömör hengerek C45 szénacélból készültek, amelyek a következő jellemzőkkel rendelkeztek: 7,85 g/cm3 sűrűség és Ra = 0,1 μm felületi érdesség (1A. ábra). A 40 mm hr magasságú gyűrűk akrilból készültek, sűrűségük 1,2 g/cm3 , felületi érdességük Ra = 0,05 μm (1B. ábra). A tömör hengerek és gyűrűk működési paramétereit, például magasságukat, átmérőjüket és tömegüket az 1. táblázat tartalmazza. A tömör hengereket az emberi test jellemzőinek a hüvelyk- és mutatóujjal megragadható tárgyak maximális tömegére gyakorolt hatásának vizsgálatára használtuk, míg a gyűrűket az emberi test jellemzőinek a hüvelyk- és mutatóujjal megragadható tárgyak maximális átmérőjére gyakorolt hatásának vizsgálatára használtuk. A többtényezős fogás-kioldási teszteket 72 órán belül, szobahőmérsékleten (24 ± 1°C, 50-55% RH) végeztük.
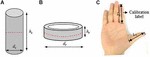
1. ábra. Megfogott tárgyméretek és kézméretek: (A) tömör henger, ahol dc és hc az átmérőt és a magasságot jelöli, (B) gyűrű, ahol dr és hra külső átmérőt és magasságot jelöli, (C) kézméretek, Li – mutatóujj hossza, Lt – hüvelykujj hossza.
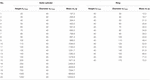
Táblázat 1

. A megragadott tárgyak geometriai jellemzői.
A résztvevők
A vizsgálatban összesen 108 önkéntest (54 férfit és 54 nőt) toboroztak a Henan Polytechnic University, a HPU óvodából és a Hexiang általános iskolából, hogy részt vegyenek a megragadás-kioldás tesztekben. Jellemzőik a következők voltak {átlag }: életkor, 11,9 (6,8) év; magasság, 141,5 (23,8) cm; hüvelykujj hossza, 41,9 (7,7) mm és mutatóujj hossza, 56,6 (10,0) mm. Minden résztvevő részletes leírást kapott a kísérlet céljairól és követelményeiről, majd a 16 év feletti résztvevőktől és a 16 év alatti résztvevők szüleitől írásbeli beleegyező nyilatkozatot kértek. Valamennyi önkéntes jobbkezes volt, normál hallással és normál látással rendelkezett, és nem volt a kórtörténetében kézsérülés, mentális betegség vagy fizikai fogyatékosság. A vizsgálatot a Bázeli Nyilatkozat elveivel és a kínai intézményi etikai bizottságok létrehozásának ajánlásaival összhangban végezték.
Műveletek
A résztvevők a vizsgálatok előtt kb. 5 perccel szappannal és vízzel megmosták a kezüket, majd törölközővel megszárították. Minden résztvevő termetét 1 mm pontossággal megmérték egy hajtogató vonalzóval. Minden résztvevőnek megkönnyítették, hogy a kezére egy kalibrációs címkét ragasztottak, és a hüvelyk- és mutatóujját kinyitották, hogy digitális fényképezőgéppel (Canon IXUS 95IS) fényképet készítsenek a tenyér tetejéről (1C. ábra). A rögzített képeket a számítógépbe továbbítottuk, majd a Digimizer 4.2.6.0 verziójával feldolgoztuk a két ujj hosszának kinyeréséhez. A hüvelykujj és a mutatóujj hosszát az ujj proximális hajlítási ráncától az adott ujj hegyéig mértük (1C. ábra), ami összhangban volt Kanchan és Krishan (2011), Ishak és munkatársai (2012) és Jee és munkatársai (2015) eredményeivel. Ezt követően a megragadott tárgyakat egy asztalra helyezték, és minden résztvevőt arra utasítottak, hogy üljön le egy irodai székre az asztal előtt úgy, hogy a jobb felkar párhuzamos legyen a törzzsel, a könyök a jobb combján nyugodjon, az alkar pedig elülső irányban kinyújtva. A résztvevőt arra kérték, hogy a jobb keze hüvelyk- és mutatóujját természetesen használva emeljen fel és mozdítson el egy tárgyat egyik helyzetből a másikba. 15 másodperccel később a résztvevő a bal kéz hüvelyk- és mutatóujjával visszatolta a tárgyat. A megragadás során a középső ujj, a gyűrűsujj, a kisujj és a tenyér nem érinthette a tárgyat.
Az emberi hüvelyk- és mutatóujj kooperatív megragadási folyamata egy kéz-agy-szem koordinációs viselkedés volt, és öt lépésre osztható (2. ábra). 1. lépés: egy tárgy helymeghatározása és érzékelése a látórendszerrel az agy vezetésével; 2. lépés: az agy feldolgozza a látórendszerből kapott információkat, és stratégiai döntést hoz (pl, előfogás típusa, fogási erő és fogási pozíció) a stabil fogás érdekében; 3. lépés: az agy parancsot ad a kéznek, hogy elérje és megragadja a tárgyat; 4. lépés: a taktilis érzékszervi információkat visszacsatolták az agynak a további döntéshozatalhoz, és ha szükséges, a fogás testtartását és erejét az agy parancsára módosítják; 5. lépés: a kéz stabilan megragadja a tárgyat, és más pozícióba mozgatja azt.
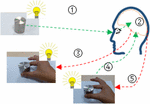
2. ábra. Az emberi hüvelykujj és mutatóujj kooperatív megragadási viselkedése.
A kísérletben a megragadott tárgyak különböző tömegű tömör hengerek (1A ábra) és különböző méretű gyűrűk (1B ábra) voltak. Minden résztvevő a tömör hengereket a tömegük alapján a könnyűtől a nehézig sorrendben fogta meg, majd a gyűrűket a külső átmérőjük alapján a kis átmérőtől a nagyig sorrendben fogta meg. Az emberi hüvelyk-mutatóujj maximális megragadó tömege jelezte a hüvelyk-mutatóujjal megragadható tárgyak maximális tömegét. Az emberi hüvelykujj-indexujj maximális megragadási átmérője a hüvelykujj-indexujjal megragadható tárgyak maximális átmérőjét jelezte. Minden egyes megragadási feladat után egy gyakorlott megfigyelő gondosan feljegyezte a megragadás eredményét, azaz a sikert vagy sikertelenséget. Egy fogási kísérletet sikeresnek minősítettünk, ha a fogás-kioldási folyamat stabil volt, és nem történt relatív csúszás a mutatóujj, a hüvelykujj és a tárgy között; ellenkező esetben sikertelen kísérletnek minősítettük. Összesen 7560 megragadási próbát (108 önkéntes × 2 kéz × 20 tömör henger + 108 önkéntes × 2 kéz × 15 gyűrű) végeztek a kísérletben.
Nemlineáris regresszióelemzés
Ez a tanulmány nemlineáris regresszióelemzési módszert alkalmaz, hogy két lehetséges matematikai modellt találjunk a függő változók (nevezetesen a maximális megragadási tömeg és a hüvelykujj-indexujj átmérője) és egy sor független változó (pl., életkor, nem, használt kéz, valamint a hüvelyk- és mutatóujj hosszának összege, a mutatóujj és a hüvelykujj hosszának aránya). Mivel az emberi hüvelyk- és mutatóujj együtt létezik, és hosszaik multikollinearitásban állnak, a regressziós elemzésben a hüvelyk- és mutatóujj hosszának jellemzésére két relatív független paramétert választottunk: a hüvelyk- és mutatóujj hosszának összegét és a mutatóujj és a hüvelykujj hosszának arányát. Tekintettel az Abdel-Malek és munkatársai (1990) által várt erős korrelációra a termet és az ujjhossz összege között, a következő regresszióelemzésben az ujjhossz összegét vették figyelembe, de a termetet nem. Az emberi test jellemzőit, mint például az életkort és a hüvelyk- és mutatóujj hosszának összegét eredeti független változóknak tekintették, és a maximális megfogó tömeget és a hüvelyk- és mutatóujj átmérőjét első, illetve második függő változóként határozták meg. A kísérletek után a lineáris (pl. y = kx) és a nemlineáris (pl., y = kx2, y = klnx) funkcionális összefüggéseket az életkor és a maximális megragadó tömeg, a hüvelykujj-indexujj hosszának összege és a maximális megragadó tömeg, az életkor és a maximális megragadó átmérő, valamint a hüvelykujj-indexujj hosszának összege és a maximális megragadó átmérő között az IBM SPSS Statistics 24.0 (24.0 verzió, IBM Corporation, Egyesült Államok) “curve estimation” programjának segítségével becsültük, majd összehasonlítottuk, hogy a két változó közötti optimális funkcionális összefüggést a korrigált R2 determinációs együttható alapján válasszuk ki. A nagyobb R2 azt jelezte, hogy a megfelelő függvénykapcsolat alkalmasabb a két változó közötti kísérleti adatok illesztésére. A konstans nem szerepelt az egyes regressziós egyenletekben.
Az eredeti mennyiségi független változók és a függő változók közötti optimális függvények megállapítása után minden egyes nem lineáris függvényt új független változónak tekintettünk, amelyet a következő többszörös lineáris regressziós elemzésben használtunk, és a szignifikancia szintet 0,05-ben állapítottuk meg. Mivel a nem és a használt kéz kategorikus változók voltak, a lineáris regresszióelemzés előtt a nem két szintjét, nevezetesen a férfi és a nő, “0”-ként és “1”-ként kódoltuk, és a használt kéz két szintjét, nevezetesen a bal kéz és a jobb kéz, szintén “0”-ként és “1”-ként kódoltuk. Végül többszörös lineáris regresszióelemzéssel két lehetséges matematikai modellt építettünk fel. A konstans nem szerepelt az egyes regressziós modellekben. Az illeszkedés jóságának tesztjét használtuk annak mérésére, hogy a megfigyelt adatok mennyire felelnek meg az egyes regressziós modelleknek, az F-tesztet használtuk az egyes regressziós modellek általános szignifikanciájának tesztelésére, a t-tesztet pedig annak megállapítására, hogy egy független változónak van-e statisztikailag szignifikáns hatása a függő változóra az egyes modellekben.
Eredmények és megbeszélés
Kísérleti eredmények leírása
A 3. ábra az emberi hüvelykujj-indexujj maximális megragadó tömegeit mutatja különböző emberi testtulajdonságok mellett (pl., nem, használt kéz, életkor és a hüvelyk- és mutatóujj hosszának összege). Ebben a vizsgálatban a résztvevők hüvelykujj-indexujjának maximális megragadó tömege 690,2 és 9859,6 g között mozgott. A férfi résztvevők hüvelykujj-indexujjának maximális megragadó tömege 5057,6 ± 2695,6 g volt (átlag ± szórás), jelentősen nagyobb, mint a női résztvevőké 3265,5 ± 1853,5 g (3A ábra). A résztvevők bal és jobb kezében azonban nem volt jelentős különbség a hüvelykujj-indexujj maximális megragadó tömegében; a bal kéz hüvelykujj-indexujjának maximális megragadó tömege 4102,7 ± 2449,4 g volt, valamivel alacsonyabb, mint a jobb kézé 4220,5 ± 2513,1 g (3B ábra). Ebben a vizsgálatban a résztvevők életkora 3∼27 év között volt, a hüvelyk- és mutatóujj hosszának összege pedig 56,9 és 132,6 mm között mozgott. Nyilvánvaló, hogy a résztvevők hüvelyk- és mutatóujjának maximális megragadó tömegei nem lineáris (pl. kvadratikus függvény, logaritmikus függvény) növekvő tendenciát mutattak az életkor és a hüvelyk- és mutatóujj hosszának összegével (3C,D ábra).
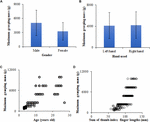
3. ábra. Az emberi hüvelyk- és mutatóujj maximális megragadó tömegei különböző emberi testtulajdonságok mellett: (A) A nem és a maximális megragadó tömeg közötti kapcsolat (átlag ± szórás), (B) a használt kéz és a maximális megragadó tömeg közötti kapcsolat (átlag ± szórás), (C) az életkor és a maximális megragadó tömeg közötti kapcsolat, (D) a hüvelykujj-indexujj hosszának összege és a maximális megragadó tömeg közötti kapcsolat.
A 4. ábra az emberi hüvelykujj-indexujj maximális megragadó átmérőjét mutatja különböző emberi testtulajdonságok mellett (pl., nem, használt kéz, életkor és a hüvelykujj-indexujj hosszának összege). Ebben a vizsgálatban a résztvevők hüvelykujj-indexujjának maximális fogási átmérője 70 és 170 mm között mozgott. A férfi résztvevők hüvelykujj-indexujjának maximális fogási átmérője 129,0 ± 22,2 mm volt, valamivel nagyobb, mint a női résztvevőké 119,9 ± 25,2 mm (4A. ábra). A bal kéz hüvelykujj-indexujj maximális fogási átmérője 124,0 ± 24,1 mm volt, ami majdnem megegyezett a jobb kézével (4B. ábra). A 3C,D ábrához hasonlóan a résztvevők hüvelyk- és mutatóujjának maximális megragadási átmérője is nem lineáris (pl. kvadratikus függvény, logaritmikus függvény) növekvő tendenciát mutatott az életkor növekedésével és a hüvelyk- és mutatóujj hosszának összegével (4C,D ábra).
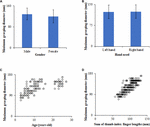
4. ábra. Az emberi hüvelyk- és mutatóujj maximális megragadási átmérője különböző emberi testtulajdonságok mellett: (A) A nem és a maximális megragadási átmérő közötti kapcsolat (átlag ± szórás), (B) a használt kéz és a maximális megragadási átmérő közötti kapcsolat (átlag ± szórás), (C) az életkor és a maximális megragadási átmérő közötti kapcsolat, (D) a hüvelykujj-indexujj hosszának összege és a maximális megragadási átmérő közötti kapcsolat.
A 2. táblázat a mennyiségi független és függő változók közötti lineáris és nemlineáris regressziós modellek korrigált determinációs együtthatóit tartalmazza. A háromféle függvénytípus korrigált determinációs együtthatóinak összehasonlításával a lineáris függvény biztosította az optimális funkcionális kapcsolatot az életkor és a maximális megragadó tömeg, valamint a hüvelykujj-indexujjak hosszának összege és a maximális megragadó átmérő között; a kvadratikus függvény a hüvelykujj-indexujjak hosszának összege és a maximális megragadó tömeg közötti optimális funkcionális kapcsolatot eredményezte; a logaritmikus függvény pedig az életkor és a maximális megragadó átmérő közötti optimális funkcionális kapcsolatot. Ezeket az eredményeket használtuk fel a következő regressziós elemzésben.

Táblázat. A független és függő változók közötti regressziós modellek korrigált determinációs együtthatói.
Az emberi hüvelykujj-indexujj maximális megragadó tömegét befolyásoló tényezők
A maximális megragadó tömeg nemtől, életkortól és a hüvelykujj-indexujj hosszának összegétől való függésének nemlineáris regressziós modelljét az 1. egyenlet mutatja be. A korrigált determinációs együttható, amelyet R2-vel jelölünk, 0,97 volt, ami arra utal, hogy a modell jól illeszkedett az adatokhoz, és azt jelzi, hogy ez a modell képes megmagyarázni a maximális megfogó tömeg szórásának 97%-át, amelyet a nem, az életkor és a hüvelykujj-indexujj hosszának összege jósolt. Az F-próbából arra következtettünk, hogy az általános illeszkedés szignifikáns (P < 0,05). t-próbák kimutatták, hogy a résztvevők által a hüvelykujj-indexujj segítségével megragadható tárgyak maximális tömege függött a nemtől, az életkortól és a hüvelykujj-indexujj hosszának összegétől (P < 0,05), de nem függött a használt kéztől és a mutatóujj és hüvelykujj hosszának arányától (P > 0.05).
amelyben Mmax – maximális fogási tömeg, g; G – nem; A – a résztvevők életkora, év; és Lo – az ujjhossz összege, mm.
A résztvevők életkora 3∼27 év között volt, ami az emberi izomzat növekedési és fejlődési szakaszában van (Lexell et al., 1992), így az életkor pozitív szignifikáns hatást mutatott az emberi hüvelykujj-indexujj maximális megfogó tömegére. A hüvelyk- és mutatóujj hosszának összege pozitív kapcsolatban állt az emberi hüvelyk- és mutatóujj maximális megragadó tömegével, aminek oka, hogy a nagy kezű résztvevők hosszú ujjakkal rendelkeznek, és általában nagy izomerővel rendelkeznek (Seo és Armstrong, 2008). A G = 0 vagy 1, azaz férfi vagy nő értékeket helyettesítettük az 1. egyenletbe, hogy leírjuk a résztvevők maximális megragadó tömegét. A férfiak és nők hüvelykujj-mutatóujj maximális megfogótömegének különbsége 1070,5 g. Hasonló kutatási eredmények azt mutatták, hogy a férfiak fogóereje szignifikánsan nagyobb, mint a nőké (Puh, 2009), és a kéz hossza jelentős hatással van az emberi ötujjasok fogóerejére (Li et al., 2010). A nem és a két ujj maximális fogótömege közötti szignifikáns kapcsolat annak tulajdonítható, hogy a férfiak maximális akaratlagos összehúzódási ereje mindig nagyobb, mint a hasonló magasságú nőké (Shurrab et al., 2017). Ezért a maximális akaratlagos összehúzódási erő növelése javíthatja az emberi két ujj maximális megragadó tömegét. A fogóerő a maximális megfogó tömeghez hasonló paraméter az emberi ujjak megfogó képességének mérésére. Ezek az eredmények azt mutatták, hogy az ujjhossz összege és a maximális akaratlagos összehúzódási erő együttesen befolyásolná a hüvelykujj-indexujj maximális megragadó tömegét, ami azt sugallta, hogy a két tényezőt együttesen kell figyelembe venni a robotkéz maximális megragadó tömegének javítása érdekében az ergonómiai tervezés során.
Az emberi hüvelykujj-indexujj maximális megragadási átmérőjét befolyásoló tényezők
A maximális megragadási átmérő életkortól, a hüvelykujj-indexujj hosszának összegétől és a mutatóujj és hüvelykujj hosszának arányától való függésének nemlineáris regressziós modelljét a 2. egyenlet mutatja be. A korrigált determinációs együttható, amelyet R2-vel jelölünk, 0,99 volt, ami azt mutatja, hogy a modell jól illeszkedett az adatokhoz, és ez a modell képes megmagyarázni a maximális megragadási átmérő varianciájának 99%-át, amelyet az életkor, a hüvelykujj-indexujjak hosszának összege és a mutatóujj és hüvelykujj hosszának aránya jósolt. Az F-tesztből arra következtettünk, hogy az általános illeszkedés szignifikáns (P < 0,05). t-tesztek azt mutatták, hogy a résztvevők által a hüvelykujj-indexujj segítségével megragadható tárgyak maximális átmérője függött az életkortól, a hüvelykujj-indexujj hosszok összegétől és a mutatóujj és hüvelykujj hosszának arányától (P < 0,05), de nem függött a nemtől és a használt kéztől (P > 0,05).
melyik Dmax – maximális fogási átmérő, mm; Lo – hüvelyk- és mutatóujj hosszának összege, mm; Lr – mutatóujj és hüvelykujj hosszának aránya.
A hüvelyk- és mutatóujj hosszának összege 56,9 és 132,6 mm között, a mutatóujj és hüvelykujj hosszának aránya pedig 1,09 és 1,65 között változott. A hüvelyk- és mutatóujj hosszának összege pozitívan arányos volt a maximális fogási átmérővel. Minél hosszabb a hüvelyk- és mutatóujj hosszának összege, annál nagyobb a két ujjhegy közötti távolság; ennélfogva annál nagyobb a hüvelyk- és mutatóujjat használó résztvevők maximális fogási átmérője. Amikor a hüvelyk- és mutatóujj hosszának összege 1 mm-rel nőtt, a hüvelyk- és mutatóujj maximális megragadási átmérője 0,98 mm-rel nőtt. Amikor a mutatóujj és a hüvelykujj hosszának aránya 0,01-gyel nőtt, a hüvelykujj-indexujj maximális fogási átmérője 0,0967 mm-rel nőtt. A mutatóujj és a hüvelykujj hosszának aránya pozitív kapcsolatban állt a maximális fogási átmérővel, ami azt jelezte, hogy a rövid hüvelykujj és a hosszú mutatóujj kombinációja növeli a hüvelykujj-indexujj maximális fogási átmérőjét. Ennek fő oka az, hogy mivel egy tárgyat két ujjal fogunk meg, különösen az erőteljes megragadás típusánál, a rövid hüvelykujj könnyen támaszpontként szolgál a hosszú mutatóujjhoz illeszkedve a tárgy kontúrjának beburkolása során, hogy egy erőzáró síkot képezzen. A rövid hüvelykujjat nem könnyen korlátozza a tárgy alakja, és a Li et al. (2013) által közölt fogásstabilitási kritérium alapján az érintkezési síkban erőzáró stabil fogás érhető el. A szakirodalomban kevés információ található erről a témáról.
Diszkusszió
Az 1. egyenlet a lásd a “Factors Affecting the Maximum Grasping Mass of Human Thumb-Index Finger” című részben kvantitatívan leírta a hüvelyk- és mutatóujj hosszának összege és a maximális megragadó tömeg közötti kapcsolatot. Egy kétujjas bionikus robotkéz kifejlesztésekor, ha a potenciális céltárgyak tömegei adottak, a robot hüvelyk- és mutatóujj optimális hosszának kialakítása levezethető az 1. egyenlet és egy további feltétel segítségével: a mutatóujj és a hüvelykujj átlagos hosszának aránya 1,36 legyen. Hasonlóképpen, a 2. egyenlet a “Factors Affecting the Maximum Grasping Diameter of Human Thumb-Index Finger” szakaszban kvantitatív módon leírta a hüvelyk- és mutatóujj hosszának összege, a mutatóujj és a hüvelykujj hosszának aránya és a maximális megragadási átmérő közötti kapcsolatot. Egy kétujjas bionikus robotkéz kifejlesztésekor, ha a potenciális céltárgyak átmérője adott, a 2. egyenlet segítségével levezethető a robot hüvelyk- és mutatóujj megfelelő hosszának kialakítása. Ezért a két nemlineáris regressziós modell hasznos volt a hüvelyk- és mutatóujj megragadási képességét reprodukálni szándékozó robotkéz optimális méretének tervezésében. Amikor egy újszerű tárgyat manipulálunk, az érzékszervi visszajelzések információt szolgáltatnak a tárgy fizikai tulajdonságairól, például a tömegéről, majd az agy feltehetően kiválasztja a központi idegrendszerünkben fenntartott, az aktuális feladathoz legmegfelelőbb modellt (Lemon és mtsai., 1995; Davidson és Wolpert, 2004). A hüvelykujj-indexujj maximális megragadó tömegkészlete alapján egy mélytanulási algoritmus fejleszthető ki annak igazolására, hogy a strukturálatlan munkakörnyezetben egyes tárgyak megfelelnek-e a bionikus robotkéz megragadási követelményeinek. Továbbá, ha vannak szabálytalan tárgyak (pl. bögre) a strukturálatlan környezetben, a hüvelykujj-indexujj maximális megragadási átmérő készlete felhasználható a bionikus robotkéz számára a szabálytalan tárgyfelületen lévő optimális megragadási helyek kiválasztására szolgáló fogástervező algoritmusok elkészítéséhez. Emellett a robotujjak kinematikai szabályozási problémáiban mindig sok időben változó probléma létezik, és a változó paraméterű konvergens differenciális neurális hálózat hatékony és pontos módszer lenne ennek a megragadástervezési problémának a megoldására (Zhang et al., 2018a, b).
Következtetés
Ebben a tanulmányban az emberi hüvelyk- és mutatóujj maximális kooperatív megragadási tömegét és átmérőjét vizsgáltuk strukturálatlan feladatok széles körében. A résztvevők életkora 3∼27 év között volt, hüvelyk- és mutatóujjuk hosszának összege pedig 56,9 és 132,6 mm között mozgott. Az eredmények azt mutatták, hogy a résztvevők hüvelyk- és mutatóujjának maximális fogási tömege és átmérője 690,2 és 9859,6 g, illetve 70 és 170 mm között mozgott. A résztvevők hüvelykujj-indexujjának maximális fogási tömege függött a nemtől, az életkortól és a hüvelykujj-indexujj hosszának összegétől (P < 0,05), de nem függött a használt kéztől és a mutatóujj és a hüvelykujj hosszának arányától (P > 0,05). A résztvevők hüvelykujj-indexujjának maximális fogási átmérője függött az életkortól, a hüvelykujj-indexujj hosszok összegétől és a mutatóujj és hüvelykujj hosszának arányától (P < 0,05), de nem függött a nemtől és a használt kéztől (P > 0,05).
Volt egy nemlineáris regressziós modell a maximális megragadó tömeg nemtől, életkortól és a hüvelykujj-indexujjhosszúságok összegétől való függésére, és egy másik nemlineáris regressziós modell a maximális megragadó átmérő életkortól, hüvelykujj-indexujjhosszúságok összegétől és a mutatóujj és hüvelykujjhosszúság arányától való függésére. A két regressziós modell hasznos volt a hüvelykujj-indexujj megragadási képességet reprodukálni kívánó robotkéz optimális méretének megtervezésében. Ez a kutatás nemcsak a bionikus robotkéz ésszerű fogási tömegének és méretének meghatározásában segíthet, hanem a kéz rehabilitációjának követelményeiben is.
Adatok hozzáférhetőségi nyilatkozata
Az e tanulmányhoz generált összes adatkészletet a cikk/kiegészítő anyag tartalmazza.
A szerzők hozzájárulása
XC és ZL tervezte és végezte a kísérleteket, valamint írta a kéziratot. YW, JL és DZ áttekintette és felügyelte a munkát.
Finanszírozás
Ezt a munkát egy európai Marie Curie nemzetközi bejövő ösztöndíj (326847 és 912847), az Északnyugati A&F Egyetem Tehetségek Speciális Alapítványa (Z111021801), a tengerentúlról visszatérők tudományos és technológiai tevékenységének Shaanxi projektje (2018030) és a Shaanxi tartomány kulcsfontosságú kutatási és fejlesztési terve (2019NY-172) támogatta.
érdekellentét
A szerzők kijelentik, hogy a kutatást olyan kereskedelmi vagy pénzügyi kapcsolatok hiányában végezték, amelyek potenciális összeférhetetlenségként értelmezhetők.
Abdel-Malek, A. K., Ahmed, A. M., El Sharkawi, S. A., és El Hamid, N. A. (1990). A termet előrejelzése kézmérésekből. Forensic Sci. Int. 46, 181-187. doi: 10.1016/0379-0738(90)90304-h
PubMed Abstract | CrossRef Full Text | Google Scholar
Bac, W., Hemming, J., Barth, R., and Wais, E. (2017). Egy paprika betakarító robot teljesítményének értékelése. J. Field Robot. 34, 1123-1139. doi: 10.1002/rob.21709
CrossRef Full Text | Google Scholar
Bansode, D. G., Borse, L. J., and Yadav, R. D. (2014). A domináns kéz fogóereje és néhány fizikai tényező közötti összefüggés vizsgálata felnőtt férfiaknál és nőknél. Int. J. Pharm. Res. Health Sci. 2, 316-323.
Google Scholar
Biegstraaten, M., Smeets, J. B. J., and Brenner, E. (2006). Az erő és a mozgás közötti kapcsolat egy tárgy precíziós fogással történő megragadásakor. Exp. Brain Res. 171, 347-357. doi: 10.1007/s00221-005-0271-z
PubMed Abstract | CrossRef Full Text | Google Scholar
Chen, X., Li, Z., Wang, Y., and Liu, J. (2019). A gyümölcs és a kéz jellemzőinek hatása a hüvelykujj-indexujj erő-fogás stabilitására a kézi gyümölcsválogatás során. Comput. Electron. Agric. 157, 479-487. doi: 10.1016/j.compag.2019.01.032
CrossRef Full Text | Google Scholar
Davidson, P. R., and Wolpert, D. M. (2004). A megragadás alapjául szolgáló belső modellek additívan kombinálhatók. Exp. Brain Res. 155, 334-340. doi: 10.1007/s00221-003-1730-z
PubMed Abstract | CrossRef Full Text | Google Scholar
Eksioglu, M. (2004). A relatív optimális fogástávolság a kéz antropometriájának függvényében. Int. J. Ind. Ergonom. 34, 1-12. doi: 10.1016/j.ergon.2004.01.007
CrossRef Full Text | Google Scholar
Feix, T., Bullock, I., and Dollar, A. M. (2014). Az emberi megragadási viselkedés elemzése: tárgyjellemzők és a megragadás típusa. IEEE Trans. Haptics 7, 311-323. doi: 10.1109/TOH.2014.2326871
PubMed Abstract | CrossRef Full Text | Google Scholar
Ishak, N. I., Hemy, N., and Franklin, D. (2012). A nem becslése kéz- és kézlenyomatméretekből egy nyugat-ausztráliai populációban. Forensic Sci. Int. 221, 154.e1-154.e6. doi: 10.1016/j.forsciint.2012.04.017
PubMed Abstract | CrossRef Full Text | Google Scholar
Jee, S. C., Bahn, S., and Yun, M. H. (2015). A nem meghatározása a koreaiak különböző kézméreteiből. Forensic Sci. Int. 257, 521.e1-521.e10. doi: 10.1016/j.forsciint.2015.10.014
PubMed Abstract | CrossRef Full Text | Google Scholar
Kanchan, T., and Krishan, K. (2011). A kéz antropometriája csonkolt maradványok nemének meghatározásában – az irodalom áttekintése. J. Forensic Leg. Med. 18, 14-17. doi: 10.1016/j.jflm.2010.11.013
PubMed Abstract | CrossRef Full Text | Google Scholar
Lemon, R. N., Johansson, R. S., and Westling, G. (1995). Kortikospinális kontroll elérés, megragadás és precíziós emelés során emberben. J. Neurosci. 15, 6145-6156. doi: 10.1523/jneurosci.15-09-06145.1995
PubMed Abstract | CrossRef Full Text | Google Scholar
Lexell, J., Sjostrom, M., Nordlund, A. S., and Taylor, C. C. (1992). Az emberi izom növekedése és fejlődése: a teljes vastus lateralis kvantitatív morfológiai vizsgálata gyermekkortól felnőtt korig. Muscle Nerve 15, 404-409. doi: 10.1002/mus.880150323
PubMed Abstract | CrossRef Full Text | Google Scholar
Li, K., Hewson, D. J., Duchene, J., and Hogrel, J. Y. (2010). A maximális fogóerő előrejelzése a kézkörfogás körméretének segítségével. Man. Ther. 15, 579-585. doi: 10.1016/j.math.2010.06.010
PubMed Abstract | CrossRef Full Text | Google Scholar
Li, Z., Li, P., Yang, H., and Wang, Y. (2013). Kétujjas paradicsom megragadásának stabilitási vizsgálatai betakarító robotok számára. Biosyst. Eng. 116, 163-170. doi: 10.1016/j.biosystemseng.2013.07.017
CrossRef Full Text | Google Scholar
Li, Z., Miao, F., Yang, Z., Chai, P., and Yang, S. (2019a). Az emberi kéz fogástípusát befolyásoló tényezők paradicsomgyümölcs-szedésnél: statisztikai vizsgálat a betakarító robot ergonómiai fejlesztéséhez. Comput. Electron. Agric. 157, 90-97. doi: 10.1016/j.compag.2018.12.047
CrossRef Full Text | Google Scholar
Li, Z., Miao, F., Yang, Z., and Wang, H. (2019b). Antropometriai vizsgálat paradicsomszüretelő robotok antropomorf tervezéséhez. Comput. Electron. Agric. 163:104881. doi: 10.1016/j.compag.2019.104881
CrossRef Full Text | Google Scholar
Luciw, M. D., Jarocka, E., and Edin, B. B. (2014). Többcsatornás eeg felvételek 3936 fogási és emelési kísérlet során változó súly és súrlódás mellett. Sci. Data 1:140047. doi: 10.1038/sdata.2014.47
PubMed Abstract | CrossRef Full Text | Google Scholar
Puh, U. (2009). Életkorral és nemmel kapcsolatos különbségek a kéz és a csípőfogás hosszában felnőtteknél. Int. J. Rehabil. Res. 33, 4-11. doi: 10.1097/MRR.0b013e328325a8ba
PubMed Abstract | CrossRef Full Text | Google Scholar
Seo, N. J., and Armstrong, T. (2008). Fogóerő, normálerő, érintkezési felület, kézméret és fogantyúméret vizsgálata hengeres fogantyúk esetében. Hum. Factors 50, 734-744. doi: 10.1518/001872008×354192
PubMed Abstract | CrossRef Full Text | Google Scholar
Shurrab, M., Mandahawi, N., and Sarder, M. D. (2017). A kétkezes csípőerő értékelése: a férfiak és nők eltérő antropometriai csípőfogási mintázatainak számszerűsítése. Int. J. Ind. Ergon. 58, 38-46. doi: 10.1016/j.ergon.2017.02.006
CrossRef Full Text | Google Scholar
Silwal, A., Davidson, J. R., Karkee, M., and Mo, C. (2017). Robotizált almaszedőgép tervezése, integrálása és terepi értékelése. J. Field Robot. 34, 1-18.
Google Scholar
Vigouroux, L., Domalain, M., and Berton, E. (2011). A tárgy szélességének hatása az izom- és ízületi erőkre a hüvelykujj-indexujj megragadásakor. J. Appl. Biomech. 27, 173-180. doi: 10.1123/jab.27.3.173
PubMed Abstract | CrossRef Full Text | Google Scholar
Wang, W., and Ahn, S. H. (2017). Alakemlékező ötvözet alapú lágy markoló változó merevséggel az engedékeny és hatékony megragadáshoz. Soft Robot. 4, 379-389. doi: 10.1089/soro.2016.0081
PubMed Abstract | CrossRef Full Text | Google Scholar
Yussof, H., and Ohka, M. (2012). Két optikai háromtengelyű tapintásérzékelővel felszerelt robotujj megragadási stratégiája és vezérlési algoritmusa. Procedia Eng. 41, 1573-1579. doi: 10.1016/j.proeng.2012.07.352
CrossRef Full Text | Google Scholar
Zhang, Z., Fu, T., Yan, Z., Jin, L., Xiao, L., Sun, Y., et al. (2018a). Változó paraméterű konvergens-differenciális neurális hálózat redundáns robotmanipulátorok közös-szögletes-drift problémáinak megoldására. IEEE ASME Trans. Mech. 23, 679-689. doi: 10.1109/tmech.2018.2799724
CrossRef Full Text | Google Scholar
Zhang, Z., Lu, Y., Zheng, L., Li, S., Yu, Z., and Li, Y. (2018b). Egy új változó paraméterű konvergens-differenciális neurális hálózat az időben változó konvex QP-probléma lineáris-egyenlőséggel korlátozott megoldására. IEEE Trans. Automat. Contr. 63, 4110-4125. doi: 10.1109/tac.2018.2810039
CrossRef Full Text | Google Scholar