Nézd meg a legújabb cikkeket

Abstract

A fény c sebességgel terjed a vákuumban, függetlenül a fényforrás mozgásától vagy a megfigyelő vonatkoztatási rendszerétől. Következésképpen a fénynek bizonyos időre van szüksége ahhoz, hogy a fényforrástól a térben lévő megfigyelőhöz eljusson, így a fénykibocsátás és a kibocsátott fény megfigyelése nem egyidejű. E megfontolások alapján a megfigyelő abszolút sebességének mérésére egy olyan módszert javasolnak, amely egy űrhajó mozgási állapotának meghatározására használható egy zárt kabin belsejéből. Ebben a tanulmányban a Lorentz-transzformáció új magyarázatát is bemutatjuk.

Kulcsszavak

koordinátarendszer, vonatkoztatási rendszer, mozgás, abszolút sebesség, relativitáselmélet, Lorentz-transzformáció, idő, tér, megfigyelő, fényforrás
A következő elemzés egy megfigyelő abszolút sebességének mérésére szolgáló gyakorlati megközelítést mutat be, amely egy űrhajó mozgási állapotának meghatározására használható egy zárt kabinból. Az abszolút sebesség fogalma általában egy fizikai rendszer különböző objektumainak szabványos, egységes sebességére utal egy olyan feltételezett mozdulatlan térhez képest, amely a benne lévő fizikai objektumoktól függetlenül létezik (azaz abszolút tér). A következőkben egy merev kinematikán alapuló megközelítést mutatunk be annak bizonyítására, hogy egy megfigyelő abszolút sebessége meghatározható abból a tényből, hogy a fény c sebességgel halad a vákuumban, függetlenül a fényforrás vagy a megfigyelő vonatkoztatási rendszerének mozgásától. Következésképpen bizonyos időre van szükség ahhoz, hogy a fény a fényforrástól a térben lévő megfigyelőhöz eljusson, így a fénykibocsátás és a kibocsátott fény megfigyelése nem egyidejű.
A javasolt elemzésben először a következő konvenciókat adjuk meg a vizsgált koordinátarendszerekre. Feltételezzük a (0,0,0,0) pontból kiinduló három páronként egymásra merőleges tengelyből álló kartéziánus koordinátarendszert, ahol a tér bármely P pontja meghatározható az x, y és z tengely mentén lévő koordinátáival, amelyeket egy rendezett valós számpárral (x,y,z) ábrázolunk. Feltételezzük, hogy az S inerciális vonatkoztatási rendszert egy (x,y,z) téglalap alakú térbeli koordináta-rendszerrel ábrázoljuk, amelynek origója O. Egy sor szabványos óra (S órákként jelölve) található az S helyhez kötött pontjain. Az S órák kölcsönösen kalibráltak (azaz azonos időpillanatban egyenértékű leolvasásokat adnak) egy fényjel adása és vétele alapján. Pontosabban, tA időpontban egy fénysugarat vetítenek az A órából a B órára, amely aztán tB időpontban a B óráról visszaverődik az A óra felé, és tA’ időpontban érkezik meg az A órához. Ha , akkor a két óra kalibrálva van. Az x,y,z koordinátákon elhelyezkedő bármely esemény t időkoordinátáját az eseményhez kapcsolódó S óra leolvasása adja. Hasonlóképpen, egy másik S’ inerciális vonatkoztatási rendszer egy második térbeli derékszögű koordinátarendszer (x’,y’,z’) alapján jön létre, amelynek origója O’, és egy másik sorozat kölcsönösen kalibrált standard órák (S’ órák) helyezkednek el az S’ vonatkoztatási rendszer helyhez kötött pontjain. Az x’,y’,z’ koordinátákban elhelyezkedő bármely esemény t’ időkoordinátáját az eseményre vonatkozó S’ óra leolvasása adja.
Mivel a tér- és időbeli koordináták eredete, valamint a koordináta tengelyek irányai nagymértékben tetszőlegesen megválaszthatók, az itt alkalmazott S és S’ közötti kapcsolatok az alábbi, az egyszerűség kedvéért alkalmazott konvenciókon alapulnak.
(1) Egy adott időpillanatban a két rendszer origója és koordinátatengelyei egymásra vannak helyezve, és az O-ban és O’-ban található órák nullára vannak állítva, azaz, .
(2) Az x és x’ tengelyek az S és S’ relatív mozgásának irányában egybeesnek; tehát x és x’ minden időpontban egybeesik, míg y és y’, valamint z és z’ párhuzamosak.
(3) S’ az S +x irányában mozog.
A javasolt elemzés azon az alapelven alapul, hogy a fény vákuumban állandó c sebességgel halad, függetlenül akár a megfigyelő, akár a fényforrás mozgásától. Ezért itt a megfigyelő U abszolút sebességét, amelyet lineárisnak és egyenletesnek feltételezünk, a következőképpen határozzuk meg: , ahol f(φ) a fényjel iránya és U iránya közötti geometriai kapcsolat függvénye, amelyet itt φ-vel jelölünk.
A javasolt elemzésben az idő és a hossz relativitásának két új magyarázatát adjuk meg, amelyek eltérnek Einstein magyarázataitól (lásd “A mozgó testek elektrodinamikájáról”). Ezeket a magyarázatokat a következő szakaszokban mutatjuk be.

Az idő relativitása

A fény véges sebességéből adódóan a fénynek bizonyos időre van szüksége ahhoz, hogy egy fényforrástól a térben lévő megfigyelőhöz eljusson. Ebből levezethető, hogy a fénykibocsátás és a fény megfigyelése nem lehet egyidejű. A fénysebesség állandósága és az 1. ábrán bemutatott feltételek alapján a következő tényezőket határozzuk meg. A fényforrás és a megfigyelő helyzete időpontban, amikor a fényforrás fényt bocsát ki (R eseményként jelölve), A és H0 értékekkel van megadva. A és közötti fényterjedési idő alatt a megfigyelő U∙T távolságot tesz meg a H0 pozíciótól H-ig, mire a megfigyelő megkapja a kibocsátott fényt. Ennek megfelelően a távolságot úgy határozzuk meg, mint a megfigyelő fényjel fogadásakor elfoglalt helyzete és a fényforrás fénykibocsátáskor elfoglalt helyzete közötti l távolságot. A fénysebesség állandósága miatt . A távolság egyenértékű az U∙T távolsággal. Végül definiáljuk a megfigyelő és a fényforrás helyzete közötti l0 távolságot. Itt bevezetjük a megfigyelő -nál lévő helyzetének figyelembevételét, amelyről korábban úgy gondoltuk, hogy nincs fizikai jelentősége. Ha a megfigyelő és a fényforrás mozgásállapota ekvivalens, akkor l0 adott, így U az ,1. ábrán ábrázolt háromszögkapcsolatok segítségével számítható ki.
A jelen munkában az esemény idejét a következő módszerrel mérjük. A megfigyelőt és az órát is az origóban helyezzük el. Amikor az esemény bekövetkeztét jelképező fényjel eléri a megfigyelőt, a fény beérkezési ideje megegyezik az óra által jelzett idővel. A megfeleltetés előnye, hogy mindig az órát alkalmazó megfigyelő helyzetére vonatkozik. Amint az 1. ábrán látható, az O3 térbeli pont a fényforrás fénykibocsátáskori pozíciója alapján, az O2 térbeli pont pedig a megfigyelő fényfogadáskori pozíciója alapján határozható meg. Nem nyilvánvaló azonban az O1 térbeli pont meghatározásának módja, amelyben a megfigyelő tartózkodik, amikor a fényforrás fényt bocsát ki. E probléma megoldására bevezetjük az abszolút nyugalom (azaz ) és az abszolút mozgás (azaz ) fogalmát. A H0 és H pontokban lévő egyetlen mozgó megfigyelőt két, az O1 és O2 térbeli pontokban nyugalomban lévő megfigyelővel H1 és H2 helyettesítjük, míg az A fényforrás az O3 térbeli pontban nyugalomban van. Mindkét megfigyelő és a fényforrás kalibrált standard órákat használ, és A fényjelet bocsát ki a időpontban, amelyet R0 eseményként jelölünk. Amikor a H1 megfigyelő fogadja a c sebességgel haladó fényjelet, az óraállás T0, amikor pedig a H2 megfigyelő fogadja, az állás T. Így a és távolságok a fényjel megfelelő futási ideje alapján a következőképpen határozhatók meg:
, (1)
és
. (2)
Az 1. ábrán látható háromszögkapcsolatok szerint az R0 esemény transzformációja a H1 és H2 megfigyelők között a következőképpen adódik:
(3)
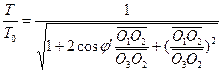(4)
Itt az O3O1 egyenes és az x tengely közötti szög, pedig az O3O2 egyenes és az x tengely közötti szög.
Visszatérve most az egyetlen mozgó megfigyelő feltételéhez, feltételezzük, hogy az S rendszerben mind a H megfigyelő, mind az A fényforrás kalibrált standard órát használ. Az R esemény pillanatában az A fényforrás az O3 térbeli pontban van, a H megfigyelő pedig az O1 pontban. Az a pillanat, amikor a fényjel eléri az O1 térbeli pontot, megfelel az S óra T0 értékének. Amikor H megfigyelő megkapja a fényjelet, a leolvasás T, és H az O2 pontban van.
Természetesen H nem tudja megfigyelni az R eseményt az O1 pontban. E probléma megoldása érdekében egy másik megfigyelőt, H-t az S rendszerben az -nak megfelelő O1 pontba helyezünk, ahol H- helyzetét az O1 térbeli pont meghatározására használjuk. Ezután az R esemény transzformációja a H- és H megfigyelők között a (3) egyenlet segítségével a következőképpen kapható.
(5)
A (3) és (4) egyenletek tehát a következőképpen írhatók át:
(6)
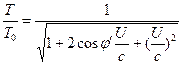(7)
e azt is megfigyelhetjük, hogy esetén a (6) és (7) egyenletek a következőkre egyszerűsödnek.
(8)
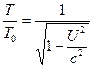(9)
A fenti elemzés alapján tehát a (6) egyenletből egyszerű módszer kapható U meghatározására, feltéve, hogy (φ) ismert.
Az egyszerűség kedvéért a megfigyelőkével egyenértékű mozgásállapotú fényforrást választjuk vonatkoztatási keretnek. Egy megfigyelőt egy egyenes, egyenletes lineáris mozgású merev rúd középpontjába helyezünk, és a rúd különböző pozícióiból érkező fényjelek különböző időpontokban érkeznek a megfigyelőhöz. A megfigyelő a rúd elhajlását a megfigyelő pozíciójában elhajlási szöggel érzékeli, amely a (8. egyenletből kapható.)
Ezzel a módszerrel egy zárt kabinból meghatározható az űrhajó mozgási állapota.

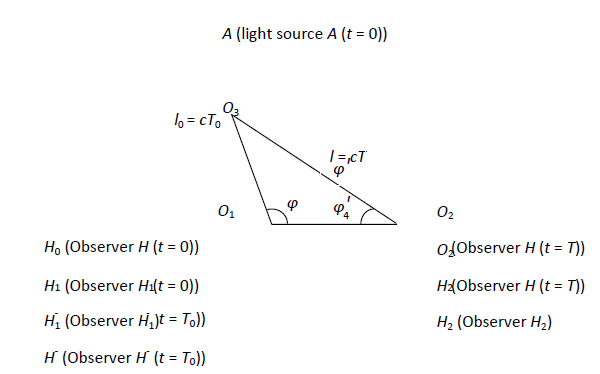
1. ábra: a megfigyelő és a fényforrás mozgási állapotai

A hossz relativitása

A fenti elemzésben két hosszat vezettünk be, azaz és . Ebben az esetben egy olyan rúd hosszát tekintjük, amelyről feltételezzük, hogy a koordinátarendszerében L hosszúságú, helyhez kötött merev rúd, amelynél az L hosszúságot egy helyhez kötött rúdmérővel mérjük, és ahol a rúd tengelye egybeesik a +x irányban U abszolút sebességgel egyenletes lineáris mozgással mozgó koordinátarendszer x tengelyével.
(a) A megfigyelő ugyanabban a mozgó koordinátarendszerben tartózkodik, mint a rúd és a pálcás mérőeszköz, és az L mérése a rúd és a pálcás mérőeszköz szuperponálásával történik.
(b) A megfigyelő több, álló koordinátákban elhelyezett, szinkronban mozgó óra segítségével egy adott t pillanatban megméri a rúd két végének helyzetét álló koordinátákban, és a két helyzet közötti távolságot az álló pálcás mérőeszközzel méri. az a) műveletből számított hossz, amelyet itt mozgó koordinátában a rúd hosszaként jelölünk. a (b) műveletből számított hossz, amelyet itt a mozgó rúd hosszaként jelölünk az álló koordinátában. Nyilvánvaló, hogy és különbözik.
Tegyük fel, hogy az S rendszerben a H- megfigyelő ugyanabban a mozgási állapotban van, mint H. Ekkor, ahogy az 1. ábrán látható, H- az O1 pontban van, amikor a fényjelet fogadja, és ezzel egyidejűleg a H megfigyelő az O4 pontban van. Ezért t=0,04
a H- és H közötti távolság , és
. (10)
a H megfigyelő által a T0 és T közötti intervallumban megtett távolság, úgy, hogy
. (11)
a H- és H közötti távolság, úgy, hogy
. (12)
Így levezethető a következő kifejezés:
(13)
A következőkben két mozgó koordinátarendszer közötti koordináta- és időbeli transzformációt vizsgálunk meg, amelyek mindketten egyenletes lineáris sebességgel mozognak, ami a Lorentz-transzformáció egy új magyarázatát jelenti.
Tegyük fel, hogy H megfigyelő (az S rendszerben), H’ megfigyelő (az S’ rendszerben) és A” fényforrás (az S” rendszerben) egyenként kalibrált standard órákat használnak, és időpontban az A” fényforrás fényjelet bocsát ki, amelyet R” eseményként jelölünk. Az R”’ esemény pillanatában A”’ az O3 pontban van, és H és H’ megfigyelők egybeesnek. Amikor H megfigyelő megkapja a fényjelet, az S óra értéke T, és H az O1 pontban van. Amikor a H’ megfigyelő megkapja a fényjelet, az S’ óra értéke T’, és H’ az O2 pontban van. Ezután az R” esemény transzformációja H’ és H megfigyelők között kiszámítható a (3. egyenletből, ahol
. (14)
Itt u a H’ és H megfigyelők közötti relatív sebesség, ami a következő transzformációkat eredményezi.
(15)
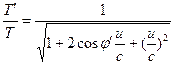(16)
A -ból a következő összefüggések vezethetők le:
. (17)
Ha és , akkor a (16) egyenlet egyszerűsödik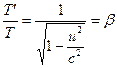
-re. (18)
Ezekből a következő transzformációs összefüggések vezethetők le:
, (19)
, (20)
, (21)
. (22)
Sőt, ha ,
, (23)
és
, (24)
, (25)
, (26)
. (27)